- Онлайн калькулятор
- Как посчитать сторону a равнобедренного треугольника
- Если известна сторона b и угол α
- Если известна сторона b и угол β
- Если известна сторона b и высота h
- Как посчитать сторону b (основание) равнобедренного треугольника
- Если известна сторона a и угол α
- Если известна сторона a и угол β
- Если известна сторона a и высота h
- Все формулы для треугольника
- 1. Как найти неизвестную сторону треугольника
- 2. Как узнать сторону прямоугольного треугольника
- 3. Формулы сторон равнобедренного треугольника
- 4. Найти длину высоты треугольника
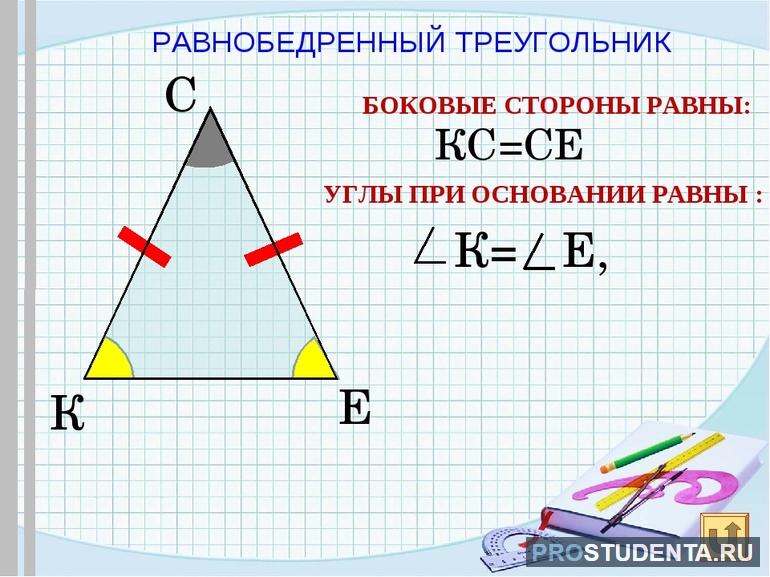
- Боковая сторона равнобедренного треугольника
- Основные свойства
- Важная теорема
- Полезные формулы
- Примеры решения задач
- 📺 Видео
Видео:Найдите сторону треугольника на рисункеСкачать

Онлайн калькулятор
Чтобы вычислить длины сторон равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):
- длину основания (b) и угол α
- длину основания (b) и угол β
- длину основания (b) и высоту (h)
- длину двух равных сторон (a) и угол α
- длину двух равных сторон (a) и угол β
- длину двух равных сторон (a) и высоту (h)
Введите их в соответствующие поля и получите результат.
Как посчитать сторону a равнобедренного треугольника
Если известна сторона b и угол α
Чему равна сторона a равнобедренного треугольника если длина основания , а угол
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол α?
Формула
Пример
Если сторона b = 10 см, а ∠α = 30°, то:
Если известна сторона b и угол β
Чему равна сторона a равнобедренного треугольника если длина основания , а угол
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол β?
Формула
Пример
Если сторона b = 10 см, а ∠β = 30°, то:
a = 10 /2⋅sin 15 = 10/(2⋅0.2588) = 19.31см
Если известна сторона b и высота h
Чему равна сторона a равнобедренного треугольника если длина основания , а высота
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и высота h?
Формула
Пример
Если сторона b = 10 см, а высота h = 20 см, то:
a = √ 1 /10 2 + 20 2 = √ 0.01+400 = 20.61см
Как посчитать сторону b (основание) равнобедренного треугольника
Если известна сторона a и угол α
Чему равна сторона b равнобедренного треугольника если длина стороны , а угол
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол α?
Формула
Пример
Если сторона a = 10 см, а ∠α = 30°, то:
b = 2⋅10⋅cos 30° = 2⋅10⋅0.8660 = 17.32см
Если известна сторона a и угол β
Чему равна сторона b равнобедренного треугольника если длина стороны , а угол
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол β?
Формула
Пример
Если сторона a = 10 см, а ∠β = 40°, то:
Если известна сторона a и высота h
Чему равна сторона b равнобедренного треугольника если длина стороны , а высота
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и высота h?
Формула
b = 2⋅ √ a 2 — h 2 , h
Пример
Если сторона a = 10 см, а высота h = 5 см, то:
Видео:№490. Найдите боковую сторону и площадь равнобедренного треугольника, если: а) основание равноСкачать
Все формулы для треугольника
Видео:№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c — стороны произвольного треугольника
α , β , γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
Видео:№157. В равнобедренном треугольнике основание больше боковой стороны на 2 см, но меньше суммы боковыСкачать
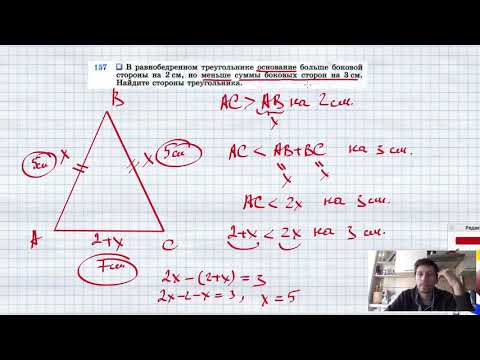
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b — катеты
c — гипотенуза
α , β — острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

4. Найти длину высоты треугольника
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

a — сторона, основание
b, c — стороны
β , γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
Видео:Найдите третью сторону треугольникаСкачать

Боковая сторона равнобедренного треугольника
У равнобедренного треугольника 2 равных по длине стороны. Каждая из них — боковая сторона равнобедренного треугольника, а третья будет основанием. Их часто просят найти при решении различных задач в геометрии. Зная основные способы решения, формулы, теоремы и свойства геометрической фигуры, учащийся может легко справиться с предложенным заданием.
Видео:Равнобедренный треугольник. 7 класс.Скачать

Основные свойства
Свойства основания равнобокого треугольника применяются на практике. Фигуру будет проще воспринимать визуально, если расположить чертеж таким образом, чтобы основание располагалось снизу.
Принято считать, что равносторонний треугольник — это частный случай равнобедренного. Каждая его сторона может считаться и основанием, и боковой.
Помимо равенства боковых сторон, при решении задач используют совпадение биссектрисы с высотой. Решить задание, как найти основание равнобедренного треугольника, зная боковые стороны, невозможно в следующих случаях:
- Известно лишь основание или углы.
- По условию дана только величина характеризующих отрезков — биссектрисы, высоты.
А также решение задачи невозможно, если заданы только две боковые стороны. В остальных случаях найти решение можно, даже если известен только один угол или площадь.
Видео:Найдите площадь равнобедренного треугольника, основание которого равно 12 см, а боковая сторона 10.Скачать

Важная теорема
Для решения задач на построение, когда задана боковая сторона треугольника, используется теорема, связанная с высотой. Применяется она и для медианы с биссектрисой.
Ее суть в следующем:
- Биссектриса, которая проведена к основанию, будет не только высотой. Она считается и медианой.
- Высота, проведенная к основанию, не только медиана. А также она может быть названа биссектрисой.
- Медиана, которая проведена к основанию, будет не только высотой, но и биссектрисой.
Теорема доказывается следующим образом: если в заданном треугольнике ABC из точки B провести высоту BD, он будет разделен на треугольники ABD и CBD. Помимо общего катета, у них равны гипотенузы. Что касается прямых AC и BD, они будут перпендикуляром.
Получается, что в ABD и CBD углы BAD и BCD, а также AB и BC равны. А также — AD и CD. Следовательно, фигуры равны, а BD считается как высотой, так и медианой и биссектрисой.
Видео:Периметр равнобедренного треугольникаСкачать

Полезные формулы
Когда по условию не даны углы, но известны все стороны, поможет формула для косинусов: cos A = (b² + с² — а²)/ 2bc = (b² + a² — а²)/2ba = b²/2ba = b/2a. При этом cos В = (а² + а² — b²)/ 2bc = (b² + a² — а²)/2а² = (2 a² — b²)/2а².
Медиана вычисляется по следующей формуле: √(2 a² + 2b² — а²)/2 = √(a² + 2b²)/2. Биссектрису можно вычислить с помощью формулы √ ab (2a+b)(a+b-a)/(a+b) = b√ a (2a+b)/(a+b).
Средняя линия, параллельная основанию равнобедренного треугольника, считается равной его половине. Равны между собой и средние линии, которые параллельны его боковым сторонам.
Если необходимо вычислить радиус описанной вокруг равнобедренного треугольника окружности, используется формула R = a²/√(4а² — b²). Когда окружность вписана в фигуру действует формула r= b/2√(2a-b)/(2a+b).
Видео:№260. Высота, проведенная к основанию равнобедренного треугольника, равна 7,6 см, а боковая сторонаСкачать

Примеры решения задач
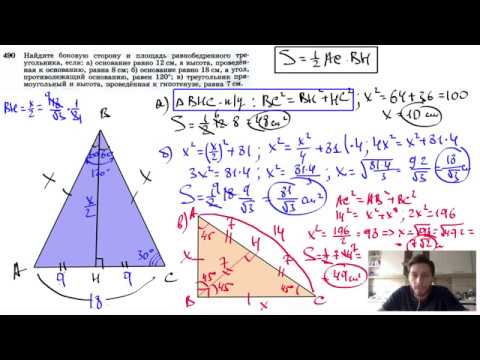
Вот примеры заданий, как узнать боковую сторону равнобедренного треугольника АВС. Так, если основание АС = 8 см, а опущенная на его середину высота (являющаяся медианой) BH =3 см, то AH = AC = 4 см. По теореме Пифагора боковая сторона AB = √ AH ² + BH ² = √ 16+9 = √25 = 5 см.
Можно привести и следующий пример задачи. Если площадь равнобедренного треугольника АВС = 40√ 3 см², а углы при основании (A и C) = 30°, угол B будет равен 180° — 2 * ∠АС = 180° — 2 * 30° = 120°.
В этом случае действует формула S = ½ АВ*АС * sin ∠B = ½ * AB ² * sin 120° = 40√ 3 см². Значит, AB ² = 2*40√ 3/ sin 120 = 80 √ 3:√ 3/2 = 160. Тогда АВ = 4√ 10 см.
Еще пример задачи — если боковая сторона равна 1, а угол при вершине 120°, диаметр окружности, описанной вокруг него, можно найти так: угол при основании будет равен (180−120)/2, то есть 30°. В таком случае диаметр будет 1/sin 30° = 2 см.
Задачи, связанные с нахождением боковой стороны треугольника, часто встречаются в геометрии. Для их решения необходимо знать перечисленные формулы и свойства.
📺 Видео
🔴 В прямоугольной трапеции основания ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Задача 6 №27621 ЕГЭ по математике. Урок 69Скачать

Геометрия Найдите боковую сторону равнобедренного треугольника площадь которого равна 36 см2 а уголСкачать

Нахождение площади равнобедренного треугольника при помощи теоремы Пифагора | Геометрия | АлгебраСкачать

№158. Основание равнобедренного треугольника равно 8 см. Медиана, проведенная к боковой сторонеСкачать

КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

Нахождение сторон равнобедренного треугольникаСкачать

Равнобедренный треугольникСкачать

Супер ЖЕСТЬ ➜ Найдите сторону треугольника ➜ Решить без тригонометрииСкачать