Видео:Как найти вектор по двум точкам?Скачать
1.5.1. Как найти вектор по двум точкам?
Если даны две точки плоскости 
и 
, то вектор 
имеет следующие координаты: 
Если даны две точки пространства 
и 
, то вектор 
имеет следующие координаты: 
То есть, из координат конца вектора нужно вычесть соответствующие координаты начала вектора. Таким образом, для противоположно направленного вектора формулы запишутся так: 
Задача 1
Даны две точки плоскости 
и 
. Найти координаты вектора 
Решение: по соответствующей формуле: 
Как вариант, можно использовать следующую запись: 
Эстеты решат и так: 
Лично я привык к первой версии записи.
Ответ: 
По условию не требовалось строить чертежа (что характерно для задач аналитической геометрии), но в целях пояснения важного момента, не поленюсь: 
И момент здесь таков:
в чём различие между координатами точек и координатами векторов?
Координаты точек – это обычные координаты в прямоугольной системе координат (единичные векторы тут вообще ни при чём). Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя.
Координаты же вектора – это его разложение по базису 
, в данном случае 
. Любой вектор является свободным, поэтому при желании мы легко можем переобозначить его через 
и отложить от какой-нибудь другой точки плоскости. Следует отметить, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости 
.
Записи координат точек 
и координат вектора 
формально одинаковы, но смысл координат абсолютно разный, и вам следует хорошо понимать эту разницу. Данное отличие, разумеется, справедливо и для пространства.
Дамы и господа, набиваем руку:
Задача 2
а) Даны точки 
и 
. Найти векторы 
и 
.
б) Даны точки 
и 
. Найти векторы 
и 
.
в) Даны точки 
и 
. Найти векторы 
и 
.
г) Даны точки 
. Найти векторы 
.
Пожалуй, достаточно…. Не пропускаем! Решаем письменно и «от руки»! Чертежи делать не нужно (коль скоро, не требовалось). Решения и ответы в конце книги.
Для проверки вычислений удобно использовать Геометрический калькулятор, приложенные к данному курсу. Дабы избежать нелепых ошибок а-ля «2 + 2 = 5». А подобные «затмения» бывают. Даже у профессоров. Отвлёкся – и студентка сбежала 🙂
Видео:Координаты вектора. 9 класс.Скачать
Упражнения на тему вычисления вектора по двум точкам на плоскости.
Эти упражнения позволят проверить, как вы умеете находить вектора по двум точкам на плоскости.
Решение задач и упражнений лучший способ проверить свои знания и закрепить пройденный материал!
Для перехода к следующему заданию нажмите кнопку «Следующий пример».
Внимание. При переходе к новому заданию этот пример станет недоступным.
Видео:9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать
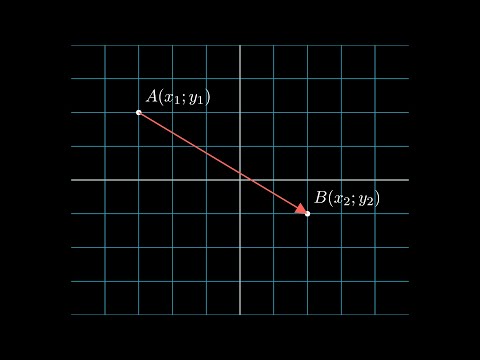
Правила. Вычисление вектора по двум точкам на плоскости.
Чтобы на плоскости найти координаты вектора AB , зная координаты его начальной точки A( x 1, y 1) и конечной точки B( x 2, y 2), необходимо из координат конечной точки вычесть координаты начальной точки:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Геометрия 9 класс (Урок№7 - Разложение вектора по двум неколлинеарным векторам. Координаты вектора.)Скачать
Определение вектора по двум точкам: онлайн-калькулятор
Чтобы найти вектор по двум точкам онлайн, нужно:
- Задать размерность вектора (двумерный или трехмерный).
- Ввести в поля координаты соответственно начальной и конечной точек.
- Нажать «рассчитать».
Определение вектора по двум точкам
Чтобы задать (определить вектор), нужно знать его начальную и конечную точки. Как определить вектор по двум точкам с помощью онлайн-калькулятора? Вот последовательность действий:
- Указываем размерность вектора. Можно выбрать вектор на плоскости (2), или вектор в пространстве (3):
Для наглядности, выберем вектор в пространстве (размерность=3)
После этого можно получить ответ и ознакомиться с решением:
🔍 Видео
Нахождение координат вектора. Практическая часть. 9 класс.Скачать
Разложение вектора по базису. 9 класс.Скачать
18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать
89. Разложение вектора по двум неколлинеарным векторамСкачать
Координаты вектора в пространстве. 11 класс.Скачать
Координаты точки и координаты вектора 1.Скачать
Векторы. Метод координат. Вебинар | МатематикаСкачать
Уравнение плоскости через 2 точки параллельно векторуСкачать
Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать
Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать
Найдите разложение вектора по векторам (базису)Скачать
1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать
РАЗЛОЖЕНИЕ ВЕКТОРА ПО ДВУМ неколлинеарным ВЕКТОРАМ 9 классСкачать
Разложение вектора по двум неколлинеарным векторам | Геометрия 7-9 класс #85 | ИнфоурокСкачать
Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать
Уравнение прямой по двум точкамСкачать
