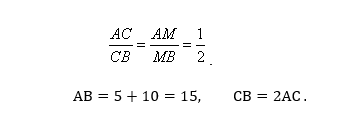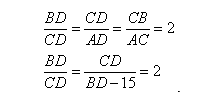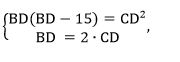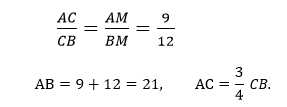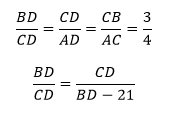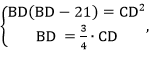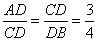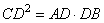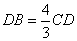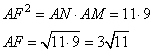Задание 25 окружности с центрами в точках (6 видео)

Задание 25 окружности с центрами в точках

Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что отрезки AB и IJ перпендикулярны.

Точка I равноудалена от A и B, поэтому она лежит на серединном перпендикуляре к отрезку AB. То же можно сказать и о J . Значит, IJ — серединный перпендикуляр к AB.

Критерии оценивания выполнения задания	Баллы
Доказательство верное, все шаги обоснованы.	2
Доказательство в целом верное, но содержит неточности.	1
Другие случаи, не соответствующие указанным критериям.	0
Максимальный балл	2

Задание 25 № 341422

Решение: IA и IB — радиусы окружности с центром в точке I => IA = IB => треугольник IAB — равнобедренный.

Проведем медиану IJ к стороне AB. Т.к. треугольник IAB — равнобедренный, то IJ также является высотой, проведённой AB => AB и IJ перпендикулярны, что и требовалось доказать.

Содержание

Репетитор по математике
Стоимость занятий
Видеокурсы подготовки к ЕГЭ-2021
Группа Вконтакте
Преимущества
Педагогический стаж
Собственная методика
Гарантированный результат
Индивидуальная работа
Задание №25 ОГЭ по математике
📹 Видео

Видео:ОГЭ по математике. Окружности с центрами в точках √25 вариант 2Скачать

Репетитор по математике

Меня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата».

Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]

Стоимость занятий

Набор на 2020/2021 учебный год открыт. Предусмотрен дистанционный формат.

Видеокурсы подготовки к ЕГЭ-2021

Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.

Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.

Видео:ОГЭ по математике. Окружности с центрами.. Вариант 3 (25)Скачать

Группа Вконтакте

В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.

Видео:ОГЭ Задание 25 Две окружностиСкачать

Преимущества

Педагогический стаж

Сейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области.

Собственная методика

За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.

Гарантированный результат

За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.

Индивидуальная работа

Все дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал.

Видео:Задача 25 ОГЭ Математика 1 ЯщенкоСкачать

Задание №25 ОГЭ по математике

Решаем сложную геометрическую задачу.

Алгоритм решения:

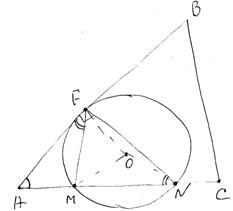
Делаем чертеж.
Определяем равенство угла между касательной и хордой и угла АВС.
Определяем соотношение отрезков из свойства биссектрисы угла треугольника и найдем АВ.
Показываем, что треугольники DAC и DCB подобны.
Составляем соотношения сторон подобных треугольников.
Составляем систему равенств.
Решаем систему.
Записываем ответ.

Решение:

2. Рассматриваем АСD. В нем:

Согласно свойству углов окружности, касательной и секущей, угол, который образован этими линиями, равен половине градусной меры дуги, заключенной между сторонами этого угла. ∠DСА равен половине градусной меры дуги АС, заключенной между его сторонами СD и СА. Но вписанный ∠СВА опирается на ту же дугу АС и по свойству вписанного угла равен половине меры этой дуги. Следовательно, ∠ СВА=∠ АСD. 3. Согласно свойству биссектрисы угла треугольника, она делит АВ на отрезки АМ и МВ, пропорциональные сторонам АС и ВС. Таким образом,

4. Рассмотрим DAC и DCB. У них:

∠ DCA = ∠ DBC по доказанному выше,

Следовательно, DAC DCB по двум углам.

5. Из определения и свойств подобных треугольников имеем:

6. Составим систему равенств:

7. Решим систему:

Ответ: 10

pазбирался: Даниил Романович | обсудить разбор | оценить

Алгоритм решения:

Сделаем чертеж.
Определим равенство углов CDB и АВС.
Определим соотношение отрезков, воспользовавшись свойством биссектрисы угла треугольника, и определим длину АВ.
Покажем, что треугольники DAC и DCB подобны.
Составим соотношения сторон подобных треугольников.
Составим систему равенств.
Решим систему.
Запишем ответ.

Решение:

2. Рассмотрим АСD. В нем, согласно свойству углов окружности, касательной и секущей, угол, который образован этими линиями, равен половине градусной меры дуги, заключенной между сторонами этого угла. ⇒∠DСА равен половине градусной меры дуги АС, заключенной между его сторонами СD и СА. Но вписанный ∠СВА опирается на ту же дугу АС и по свойству вписанного угла равен половине меры этой дуги. Следовательно, ∠ СВА=∠ АСD. 3. Согласно свойству биссектрисы угла треугольника, согласно которому она делит АВ на отрезки АМ и МВ, пропорциональные сторонам АС и ВС. Таким образом,

4. Рассмотрим DAC и DCB. У них:

∠ DCA = ∠ DBC по доказанному выше,

Значит, DAC DCB по двум углам.

5. Из определения и свойств подобных треугольников имеем:

6. Составим систему равенств:

7. Решим систему:

Так как AD = DB-21, имеем:

Таким образом, искомая длина CD=36.

pазбирался: Даниил Романович | обсудить разбор | оценить

Алгоритм решения:

Сделаем чертеж.
Установим подобие треугольников AFM и ANF.
Определим сторону FM.
Определим ∠FNA.
Найдем .
Составим теорему синусов и найдем радиус окружности.
Запишем ответ.

Решение:

1. Рассмотрим треугольники AFM и ANF. У них:

Угол A является общим, а

по доказанному выше.

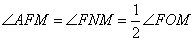
Следовательно, треугольник AFM подобен треугольнику ANF по двум углам. Отсюда вытекает:

3. В треугольнике AFM сторона AF=3, сторона AM=9. Воспользуемся теоремой косинусов для определения FM:

Полученное значение означает, что AFM является равнобедренным. У него основание AF. 4. По свойству равнобедренного треугольника ∠FAM=∠AFM. Отсюда 5. Найдем Значит, 6. Из FMN по теореме синусов: где R – радиус описанной окружности. Отсюда получим значение радиуса окружности: Ответ: 5,4

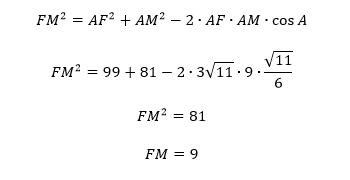
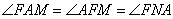
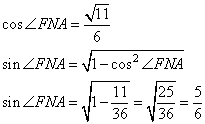
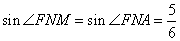
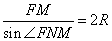
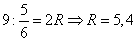
pазбирался: Даниил Романович | обсудить разбор | оценить

Пусть O — центр данной окружности, а Q — центр окружности, вписанной в треугольник ABC .

Точка касания M окружностей делит AC пополам по условию.

Лучи AQ и AO — биссектрисы смежных углов, так как касательные к окружностям равноудалены от центра. Так как AQ и AO — биссектрисы смежных углов, то угол OAQ прямой — смежные углы в сумме дают 180°, значит сумма их биссектрис:

Далее рассмотрим прямоугольный треугольник OAQ. По свойству высоты в прямоугольном треугольнике, получаем:

AM² = MQ•MO Отсюда:

pазбирался: Даниил Романович | обсудить разбор | оценить

Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 90 0 .

Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.

Составим отношение сторон:

A E A B . . = A B A F . . откуда по свойству пропорции АВ 2 =АЕ ∙ АF

Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.

Составим отношение сторон:

A E A D . . = A C A F . . ; откуда выразим AD= A E ∙ A F А C . . = A E ∙ A F A C . .

Теперь рассмотрим наши два полученных равенства: АВ 2 =АЕ ∙ АF и AD= A E ∙ A F A C . .

Видим, что 36 2 =АЕ ∙ АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD= A E ∙ A F A C . . = 36 2 54 . . = 24

Теперь найдем CD=AC-AD=54-24=30

pазбирался: Даниил Романович | обсудить разбор | оценить