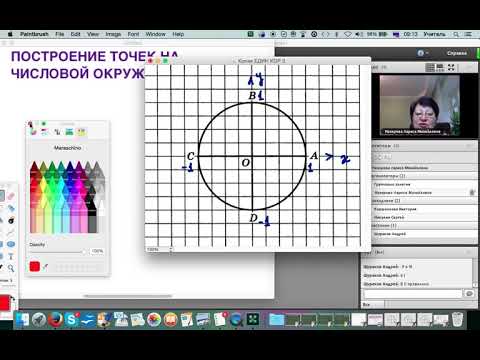
Если посмотреть на числовую окружность , то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).

(() (frac) (;2π)) — четвертая четверть
- Почему так важно определять какой четверти принадлежит угол?
- Про непостоянство четвертей:
- Как определить четверти на числовой окружности
- Четверть числовой окружности
- Почему так важно определять какой четверти принадлежит угол?
- Про непостоянство четвертей:
- Единичная числовая окружность на координатной плоскости
- п.1. Понятие тригонометрии
- п.2. Числовая окружность
- п.3. Градусная и радианная мера угла
- п.4. Свойства точки на числовой окружности
- п.5. Интервалы и отрезки на числовой окружности
- п.6. Примеры
- 1. Конспект для учителя по теме «Числовая окружность»
- Как определить какой четверти принадлежит число на числовой окружности
- 📽️ Видео
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Почему так важно определять какой четверти принадлежит угол?
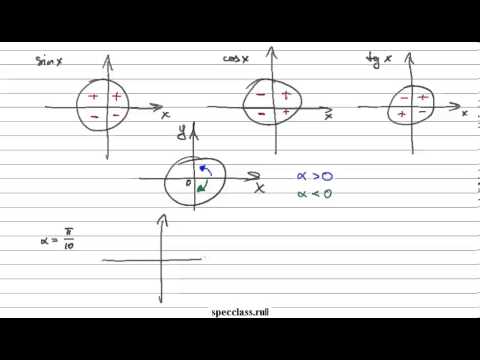
Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций .
Например, для любого угла из второй четверти — синус положителен, а косинус , тангенс и котангенс отрицательны. А для любого угла из первой четверти — все четыре функции будут положительны.
Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.
Пример (ЕГЭ):
 ((0;-) (frac) ()) — четвертая четверть Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную. Видео:Как искать точки на тригонометрической окружности.Скачать  Как определить четверти на числовой окружностиВидео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать  Четверть числовой окружностиЕсли посмотреть на числовую окружность , то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки). |  (() (frac ) (;2π)) — четвертая четверть Видео:В какой четверти находится точка единичной окружности, полученная при повороте Ро(1;0) на угол...Скачать  Почему так важно определять какой четверти принадлежит угол?Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций . Например, для любого угла из второй четверти — синус положителен, а косинус , тангенс и котангенс отрицательны. А для любого угла из первой четверти — все четыре функции будут положительны. Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти. Нам известен косинус, а найти нужно синус того же угла. Какая тригонометрическая формула связывает синус и косинус того же угла? Подставим известное, и проведем вычисления. Видео:Точки на числовой окружностиСкачать  Про непостоянство четвертей:Важно понимать, что, например, первой четверти принадлежат не только углы от (0) до (frac ) , но и углы от (2π) до (frac ) , и от (4π) до (frac ) , и от (6π) до (frac ) и так далее. Ведь как только мы заканчиваем полный оборот – кончается четвертая четверть и опять начинается первая. Кроме того, нужно помнить, что углы могут откладываться в отрицательную сторону (по часовой стрелке), и тогда мы попадем в первую четверть только в конце круга. Ведь сначала мы пройдем четвертую четверть, потом в третью и т.д. |  ((0;-) (frac ) ()) — четвертая четверть Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную. Видео:Числовая окружностьСкачать  Единичная числовая окружность на координатной плоскостип.1. Понятие тригонометрииТригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами. Базовым объектом изучения в тригонометрии является угол. Предметом изучения тригонометрии как раздела математики выступают: п.2. Числовая окружностьМы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
п.3. Градусная и радианная мера углаУглы можно измерять в градусах или в радианах. В целом, более обоснованной и естественной для измерения углов является радианная мера.
п.4. Свойства точки на числовой окружностиПостроим числовую окружность. Обозначим O(0;0), A(1;0)
п.5. Интервалы и отрезки на числовой окружностиКаждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.
п.6. ПримерыПример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2. Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^ =frac .\ EC=60^ =frac .\ AE=EC+CD=90^ +30^ =120^ =frac .\ ED=EC+CD=60^ +90^ =150^ =frac . end Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac ; frac ; frac ; frac ).
Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac ; 5pi; frac ; frac ).
Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.
(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb )), запишите количество полученных базовых точек.
Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам. Видео:Длина дуги числовой окружности | Алгебра 10 класс #9 | ИнфоурокСкачать  1. Конспект для учителя по теме «Числовая окружность»Что такое числовая окружность? Для чего она нужна? Очень часто термины тригонометрический круг, единичная окружность, числовая окружность плохо понимаются. И совершенно зря. Эти понятия – мощный и универсальный помощник во всех разделах тригонометрии. Фактически, это легальная шпаргалка! Нарисовал тригонометрический круг – и сразу увидел ответы! Заманчиво? Сегодня мы будем учиться использовать единичную окружность. Для успешной работы с единичной окружностью нужно знать всего три вещи. Первое. Надо знать, что такое синус, косинус, тангенс и котангенс в применении к прямоугольному треугольнику. Второе. Надо знать, что такое тригонометрический круг, единичная окружность, числовая окружность. Третье. Надо знать, как отсчитывать углы на тригонометрическом круге, и что такое градусная и радианная меры углов.
Угол поворота – это угол, полученный вращением луча около его начала О от начального положения ОА до конечного положения ОВ.
Угол в 1
Угол в 1 радиан — это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности.
В зависимости от того в какой координатной четверти окажется начальный радиус, угол α называют углом этой четверти: 0 Видео:Найти знак тригонометрической функции (bezbotvy)Скачать Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам. Единичной окружностью называют окружность радиуса 1. Общий вид числовой окружности. 1) Ее радиус принимается за единицу измерения. 2) Горизонтальный и вертикальный диаметры делят числовую окружность на четыре четверти (см.рисунок). Их соответственно называют первой, второй, третьей и четвертой четвертью. 3) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка. первая четверть – это дуга AB вторая четверть – дуга BC третья четверть – дуга CD четвертая четверть – дуга DA 4) Начальная точка числовой окружности – точка А. Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки. Центр радиуса числовой окружности соответствует началу координат (числу 0). Горизонтальный диаметр соответствует оси x, вертикальный – оси y. Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0). Значения x и y в четвертях числовой окружности: x 0, y Основные величины числовой окружности: Имена и местонахождение основных точек числовой окружности: Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности. Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2π) против часовой стрелки. 1) Начнем с крайних точек на осях координат. Начальная точка – это 2π (крайняя правая точка на оси х, равная 1). Как вы знаете, 2π – это длина окружности. Значит, половина окружности – это 1π или π. Ось х делит окружность как раз пополам. Соответственно, крайняя левая точка на оси х, равная -1, называется π. Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность – это π, то половина полуокружности – это π/2. Одновременно π/2 – это и четверть окружности. Отсчитаем три таких четверти от первой до третьей – и мы придем в крайнюю нижнюю точку на оси у, равной -1. Но если она включает три четверти – значит имя ей 3π/2. 2) Теперь перейдем к остальным точкам. Обратите внимание: все противоположные точки имеют одинаковый числитель – причем это противоположные точки и относительно оси у, и относительно центра осей, и относительно оси х. Это нам и поможет знать их значения точек без зубрежки. Надо запомнить лишь значение точек первой четверти: π/6, π/4 и π/3. И тогда мы «увидим» некоторые закономерности: — Относительно оси у в точках второй четверти, противоположных точкам первой четверти, числа в числителях на 1 меньше величины знаменателей. К примеру, возьмем точку π/6. Противоположная ей точка относительно оси у тоже в знаменателе имеет 6, а в числителе 5 (на 1 меньше). То есть имя этой точки: 5π/6. Точка, противоположная π/4, тоже имеет в знаменателе 4, а в числителе 3 (на 1 меньше, чем 4) – то есть это точка 3π/4. Точка, противоположная точке π/4, тоже имеет в знаменателе 4, а в числителе число на 1 больше: 5π/4. — Относительно оси х (четвертая четверть) дело посложнее. Здесь надо к величине знаменателя прибавить число, которое на 1 меньше – эта сумма и будет равна числовой части числителя противоположной точки. Начнем опять с π/6. Прибавим к величине знаменателя, равной 6, число, которое на 1 меньше этого числа – то есть 5. Получаем: 6 + 5 = 11. Значит, противоположная ей относительно оси х точка будет иметь в знаменателе 6, а в числителе 11 – то есть 11π/6. Точка π/4. Прибавляем к величине знаменателя число на 1 меньше: 4 + 3 = 7. Значит, противоположная ей относительно оси х точка имеет в знаменателе 4, а в числителе 7 – то есть 7π/4. 3) Еще одна закономерность для точек середин четвертей. Понятно, что их знаменатель равен 4. Обратим внимание на числители. Числитель середины первой четверти – это 1π (но 1 не принято писать). Числитель середины второй четверти – это 3π. Числитель середины третьей четверти – это 5π. Числитель середины четвертой четверти – это 7π. Получается, что в числителях середин четвертей – четыре первых нечетных числа в порядке их возрастания: Особенности числовой окружности. Сравнение с числовой прямой. Как вы знаете, на числовой прямой каждая точка соответствует единственному числу. К примеру, если точка А на прямой равна 3, то она уже не может равняться никакому другому числу. На числовой окружности все иначе, поскольку это окружность. К примеру, чтобы из точки А окружности прийти к точке M, можно сделать это, как на прямой (только пройдя дугу), а можно и обогнуть целый круг, а потом уже прийти к точке M. Вывод: Пусть точка M равна какому-то числу t. Как мы знаем, длина окружности равна 2π. Значит, точку окружности t мы можем записать двояко: t или t + 2π. Это равнозначные величины. Отсюда формула: Если точка M числовой окружности равна числу t, то она равна и числу вида t + 2πk, где k – любое целое число: M(t) = M(t + 2πk), где k ∈ Z. Число k называется параметром. Уравнение числовой окружности Промежутки на числовой окружностиСкачать Определение значений по точкам на числовой окружностиСкачать Тригонометрическая окружность. Как выучить?Скачать Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать Алгебра 10 класс. 15 сентября. Числовая окружность #1Скачать Как найти координаты точек на тригонометрической окружностиСкачать 10 класс - Алгебра - Числовая окружностьСкачать Математика 10 класс.Построение точек на числовой окружности 10 классСкачать 1. Числовая окружность. 10 классСкачать АЛГЕБРА 10 класс: Числовая окружность. Общие понятия | ВидеоурокСкачать 10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||























 ?
? части окружности.
части окружности.

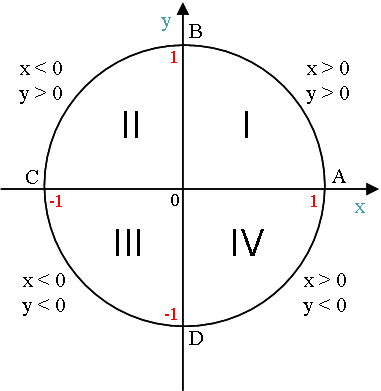 Числовая окружность на координатной плоскости.
Числовая окружность на координатной плоскости.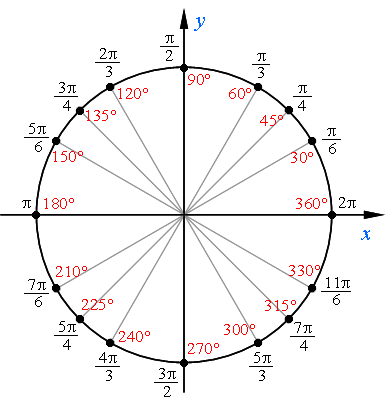
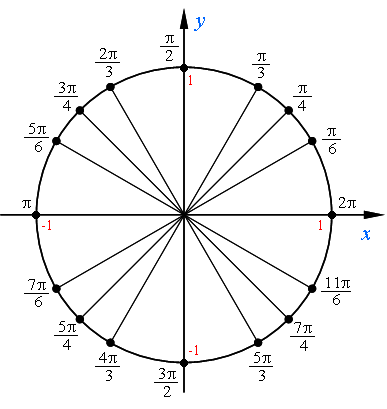
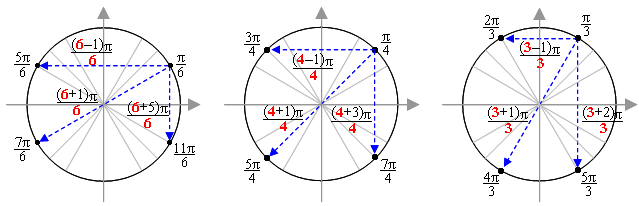 — Относительно центра осей координат все наоборот: числа в числителях противоположных точек (в третьей четверти) на 1 больше значения знаменателей. Возьмем опять точку π/6. Противоположная ей относительно центра точка тоже имеет в знаменателе 6, а в числителе число на 1 больше – то есть это 7π/6.
— Относительно центра осей координат все наоборот: числа в числителях противоположных точек (в третьей четверти) на 1 больше значения знаменателей. Возьмем опять точку π/6. Противоположная ей относительно центра точка тоже имеет в знаменателе 6, а в числителе число на 1 больше – то есть это 7π/6.