Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
- Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
- Решу ОГЭ 2022 тренировочный вариант №37446025 по математике 9 класс с ответами
- ПОДЕЛИТЬСЯ
- Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37446025:
- Ответы и решения для заданий ОГЭ 2022
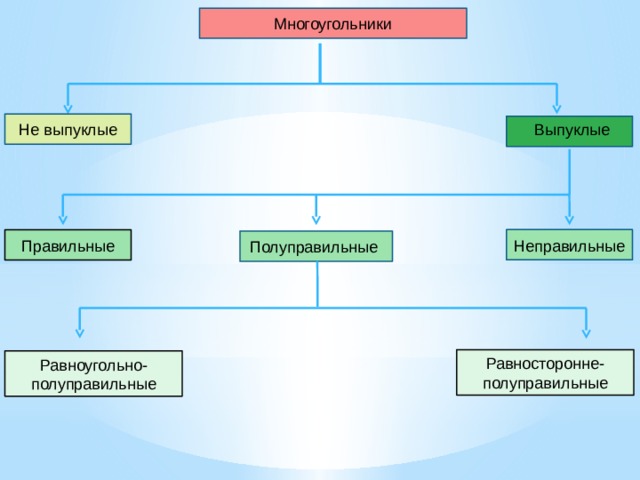
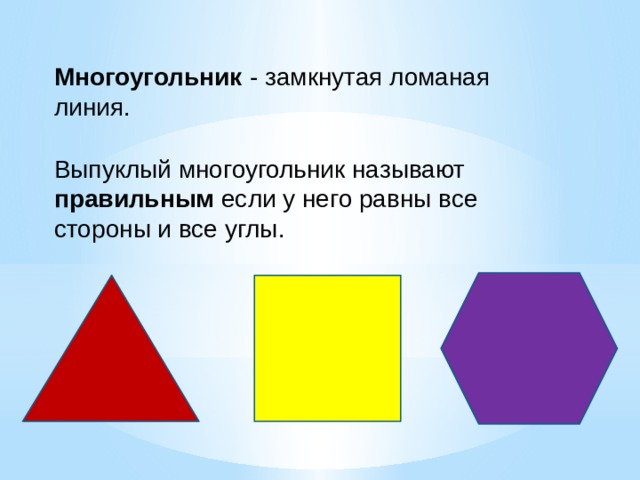
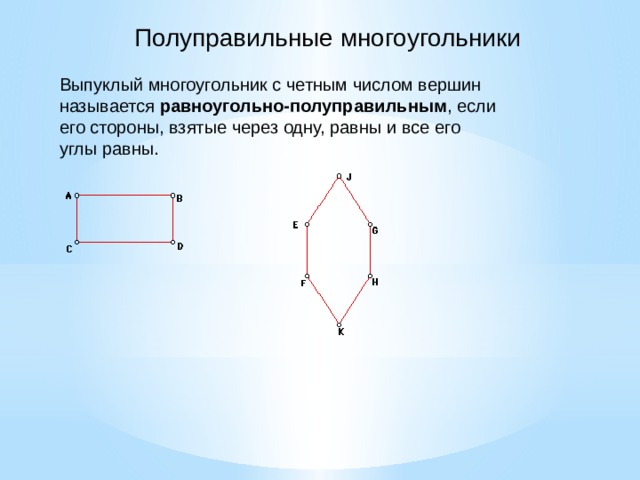
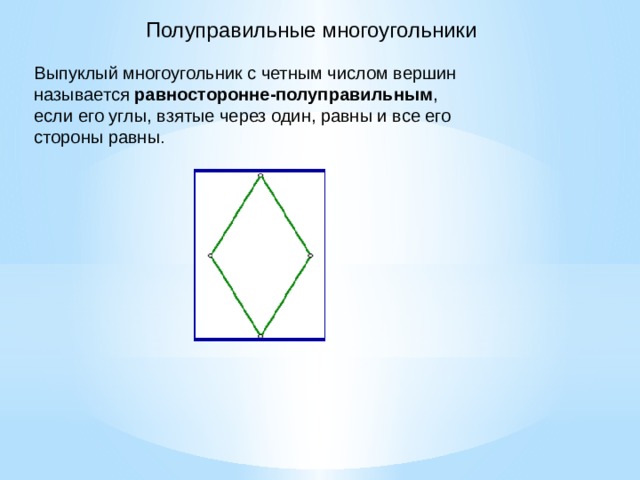
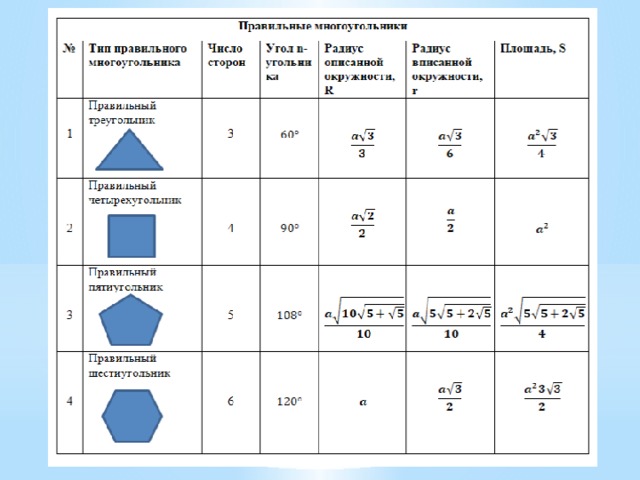
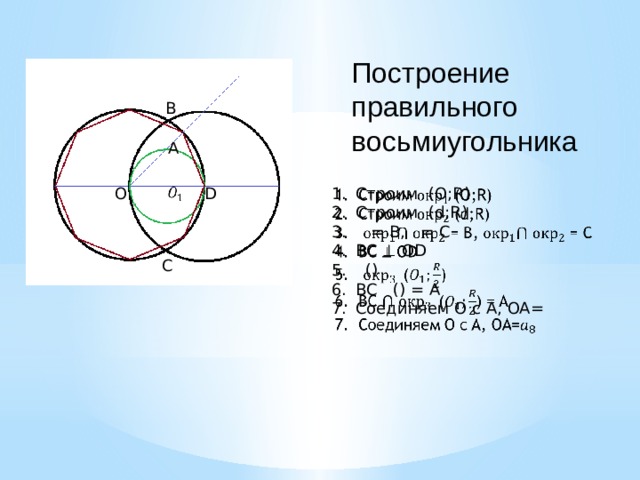
- Правильные многоугольники
- Просмотр содержимого документа «Сборник задач по геометрии»
- Просмотр содержимого презентации «Презентация»
- 📸 Видео
Видео:Задание 16 ОГЭ 2023 математика | Окружность, круг и их элементыСкачать
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Карточки для подготовки к ОГЭ 9 класс
Составила: учитель математики
Шмакова Татьяна Валерьевна
Задание 10 № 311503. В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC . 
Построим OA и OC радиусы. Центральный угол AOC равен 360°:8 = 45°. Угол ABC — вписанный и опирается на ту же дугу, поэтому он равен 45°:2 = 22,5°. Ответ: 22,5.
Задание 10 № 339483. Окружность с центром в точке O описана около равнобедренного треугольника ABC , в котором AB = BC и ∠ ABC = 177°. Найдите величину угла BOC . Ответ дайте в градусах. 
Сумма углов треугольника равна 180°. Треугольник 
— равнобедренный, следовательно, 
Угол 
— вписанный, поэтому он равен половине дуги, на которую опирается. Угол 
— центральный, поэтому он равен величине дуги, на которую опирается. Углы и опираются на одну и ту же дугу, следовательно, 
Ответ: 3.
Задание 10 № 341116. Окружность с центром в точке O описана около равнобедренного треугольника ABC , в котором AB = BC и ∠ ABC = 66°. Найдите величину угла BOC . Ответ дайте в градусах. 
Сумма углов треугольника равна 180°. Треугольник — равнобедренный, следовательно, 
Угол — вписанный, поэтому он равен половине дуги, на которую опирается. Угол — центральный, поэтому он равен величине дуги, на которую опирается. Углы и опираются на одну и ту же дугу, следовательно, 
Ответ: 114.
Задание 10 № 339828. Четырехугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD . Ответ дайте в градусах. 
Угол ABC — вписанный, опирается на дугу ADC , поэтому величина дуги ADC равна 2 · 70° = 140°. Угол CAD — вписанный, опирается на дугу CD , поэтому величина дуги CD равна 2 · 49° = 98°. Угол ABD — вписанный, опирается на дугу AD , поэтому ∠ ABD = ∪ AD /2 = ( ∪ ADC − ∪ CD )/2 = (140° − 98°)/2 = 21°. Ответ: 21.
Задание 10 № 341707. Найдите площадь квадрата, описанного вокруг окружности радиуса 7.
Пусть 
и 
соответственно радиус и диаметр окружности, 
— сторона квадрата. Сторона квадрата равна диаметру вписанной окружности. Найдём площадь квадрата: 
Ответ: 196.
Задание 10 № 316346. Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
Решение. Воспользуемся теоремой косинусов:
Здесь и 
— боковые стороны равнобедренного треугольника, 
— основание.
Диаметр описанной окружности вычислим по формуле: 
Задание 10 № 311410. Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC , если BD = 1 см, а радиус окружности равен 5 см. 
Найдем отрезок DO : DO = OB − BD = 5 − 1 = 4. Так как OB перпендикулярен AC , треугольник AOD — прямоугольный. По теореме Пифагора имеем: 
. Треугольник AOC — равнобедренный так как AO = OC = r , тогда AD = DC . Таким образом, AC = AD ·2 = 6. Ответ: 6.
Задание 10 № 311488. Найдите величину (в градусах) вписанного угла α , опирающегося на хорду AB , равную радиусу окружности. 
Проведем радиусы OA и OB . Так как по условию задачи хорда AB равна радиусу, то треугольник AOB — равносторонний, следовательно, все его углы равны 60°. Угол AOB — центральный и равен 60° Угол ACB — вписанный и опирается на ту же дугу, что и угол AOB . Таким образом, 
Ответ: 30.
Задание 10 № 311681. К окружности с центром в точке О проведены касательная AB и секущая AO . Найдите радиус окружности, если AB = 12 см, AO = 13 см. 
Соединим отрезком точки O и B ; полученный отрезок — радиус, проведённый в точку касания, поэтому OB перпендикулярен AB . Задача сводится к нахождению катета OB прямоугольного треугольника AOB : по теореме Пифагора равен 5 см. Ответ: 5.
Задание 10 № 311912.
В треугольнике ABC угол C равен 90°, AC = 30 , BC = 
Найдите радиус окружности, описанной около этого треугольника. 
Вписанный прямой угол опирается на диаметр окружности, поэтому радиус окружности, описанной вокруг прямоугольного треугольника, равен половине гипотенузы. По теореме Пифагора имеем: 
Ответ: 17,5.
Задание 10 № 324868. Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14. 
Пусть первая дуга имеет градусную меру 
тогда вторая дуга имеет градусную меру 
а третья — 
Три дуги в сумме составляют окружность, поэтому получаем:
Поэтому меньшая дуга окружности равна 
Угол треугольника, опирающийся на эту дугу является вписанным, поэтому он равен половине дуги: 
Меньший угол треугольника лежит против меньшей стороны. Найдём радиус описанной окружности:
Ответ: 14.
Задание 10 № 311503. В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC .
Задание 10 № 316346. Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
Задание 10 № 339483. Окружность с центром в точке O описана около равнобедренного треугольника ABC , в котором AB = BC и ∠ ABC = 177°. Найдите величину угла BOC . Ответ дайте в градусах.
Задание 10 № 339828. Четырехугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD . Ответ дайте в градусах.
Задание 10 № 341707. Найдите площадь квадрата, описанного вокруг окружности радиуса 7.
Задание 10 № 311503. В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC .
Задание 10 № 316346. Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
Задание 10 № 339483. Окружность с центром в точке O описана около равнобедренного треугольника ABC , в котором AB = BC и ∠ ABC = 177°. Найдите величину угла BOC . Ответ дайте в градусах.
Задание 10 № 339828. Четырехугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD . Ответ дайте в градусах.
Задание 10 № 341707. Найдите площадь квадрата, описанного вокруг окружности радиуса 7.
1) Геометрия. Учебник для 7 класса общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев. Научный редактор – академик А.Н. Тихонова. — 22-е изд. – М.: Просвещение, 2013.
2). Сборник для подготовки ОГЭ. И.В. Ященко, С.А.Шестаков, А.В. Семенов.
3) Сайт: http://www fipi..ru
4) Сайт: http://alexlarin.net/ для подготовки ОГЭ
5) Сайт: открытый банк заданий для подготовки ОГЭ по математике.
Видео:Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать
Решу ОГЭ 2022 тренировочный вариант №37446025 по математике 9 класс с ответами
ПОДЕЛИТЬСЯ
Сентябрьский тренировочный вариант (тренировочная работа) №37446025 решу ОГЭ 2022 года по математике 9 класс с ответами и решением для подготовки к экзамену, вариант составлен по новой демоверсии ФИПИ.
Ссылка для скачивания варианта: задания (КИМ)
Ответы и решения для варианта: скачать
Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37446025:
Ответы и решения для заданий ОГЭ 2022
Каждый водитель в Российской Федерации должен быть застрахован по программе обязательного страхования гражданской ответственности (ОСАГО). Стоимость полиса получается умножением базового тарифа на несколько коэффициентов. Коэффициенты зависят от водительского стажа, мощности автомобиля, количества предыдущих страховых выплат и других факторов. Коэффициент бонус-малус (КБМ) зависит от класса водителя. Это коэффициент, понижающий или повышающий стоимость полиса в зависимости от количества ДТП в предыдущий год. Сначала водителю присваивается класс 3. Срок действия полиса, как правило, один год. Каждый последующий год класс водителя рассчитывается в зависимости от числа страховых выплат в течение истекшего года, в соответствии со следующей таблицей.
Задание 1 №369848 Вячеслав страховал свою гражданскую ответственность два года. В течение первого года была сделана одна страховая выплата, после этого выплат не было. Какой класс будет присвоен Вячеславу на начало третьего года страхования?
Ответ: 2
Задание 2 №369849 Чему равен КБМ на начало третьего года страхования?
Ответ: 1,4
Задание 3 №369850 Коэффициент возраста и водительского стажа (КВС) также влияет на стоимость полиса (см. таблицу). Когда Вячеслав получил водительские права и впервые оформил полис, ему было 23 года. Чему равен КВС на начало 3-го года страхования?
Ответ: 1,63
Задание 4 №369851 В начале второго года страхования Вячеслав заплатил за полис 27 435 руб. Во сколько рублей обойдётся Вячеславу полис на третий год, если значения других коэффициентов (кроме КБМ и КВС) не изменятся?
Ответ: 22820
Задание 5 №369852 Вячеслав въехал на участок дороги протяжённостью 3,3 км с камерами, отслеживающими среднюю скорость движения. Ограничение скорости на дороге — 80 км/ч. В начале и в конце участка установлены камеры, фиксирующие номер автомобиля и время проезда. По этим данным компьютер вычисляет среднюю скорость на участке. Вячеслав въехал на участок в 10:05:08, а покинул его в 10:07:20. Нарушил ли Вячеслав скоростной режим? Если да, на сколько км/ч средняя скорость на данном участке была выше разрешённой?
Ответ: 10
Задание 10 №325288 Средний рост жителя города, в котором живет Даша, равен 170 см. Рост Даши 173 см. Какое из следующих утверждений верно? 1) Даша — самая высокая девушка в городе. 2) Обязательно найдется девушка ниже 170 см. 3) Обязательно найдется человек ростом менее 171 см. 4) Обязательно найдется человек ростом 167 см.
Ответ: 3
Задание 14 №394399 Мать дарит каждой из пяти своих дочерей в день рождения, начиная с пяти лет, столько книг, сколько дочери лет. Возрасты пяти дочерей составляют арифметическую прогрессию, разность которой равна 2. Сколько лет было старшей дочери, когда у них составилась библиотека общей численностью в 495 книг?
Ответ: 18
Задание 15 №132775 Один угол параллелограмма в два раза больше другого. Найдите меньший угол. Ответ дайте в градусах.
Ответ: 60
Задание 16 №311503 В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.
Ответ: 22,5
Задание 18 №341709 На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AC.
Ответ: 4
Задание 19 №341525 Какие из следующих утверждений верны? 1) Треугольника со сторонами 1, 2, 4 не существует. 2) Сумма углов любого треугольника равна 360 градусам. 3) Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности.
Ответ: 13
Задание 21 №314395 Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?
Ответ: 2:1
Задание 23 №311710 Найдите площадь выпуклого четырёхугольника с диагоналями 3 и 4, если отрезки, соединяющие середины его противоположных сторон, равны.
Ответ: 6
Задание 25 №340237 На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC = 12, BC = 18 и CD = 8.
Видео:ОГЭ 2023 математика 16 задание окружность квадрат площадьСкачать
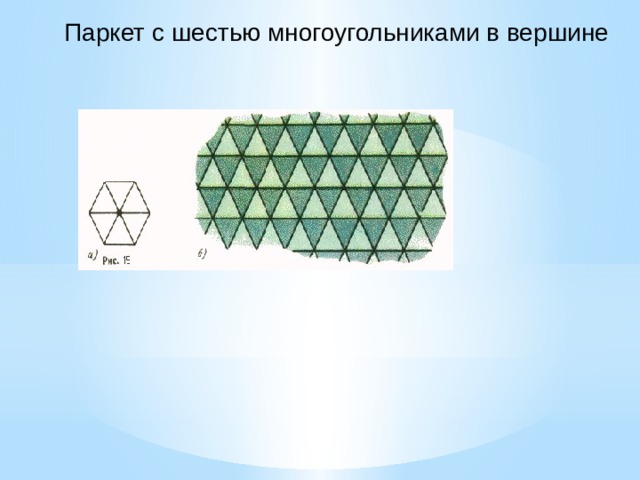
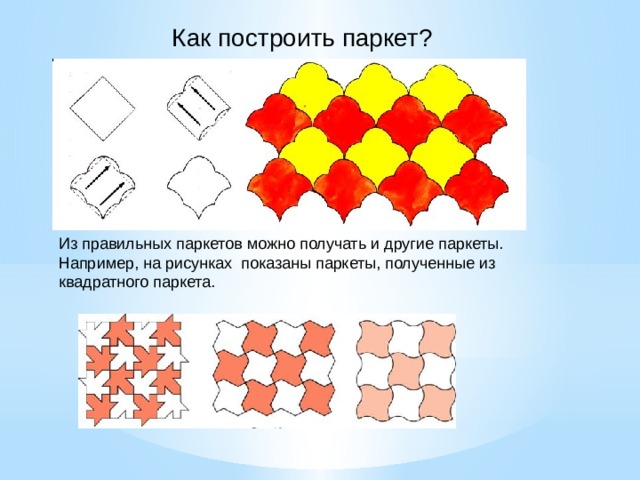
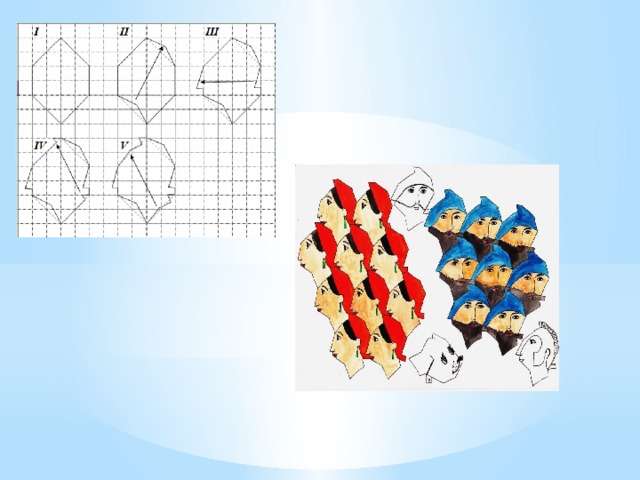
Правильные многоугольники
Крайне малое количество часов в школьном курсе математики принадлежит теме правильные многоугольники. Это несправедливым. Ведь правильные многоугольники занимают особое место в нашей жизни. Человек проявляет интерес к многоугольникам с самого раннего детства. Именно столь крайне красивые фигуры повсеместно встречаются в научной теории и таких видах искусства как живопись и архитектура.
Просмотр содержимого документа
«Сборник задач по геометрии»
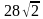. Найдите длину стороны этого квадрата.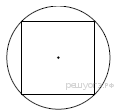
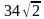. Найдите длину стороны этого квадрата.
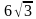. Найдите радиус окружности, описанной около этого треугольника.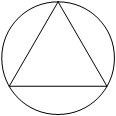
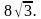Найдите радиус окружности, описанной около этого треугольника.
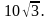Найдите радиус окружности, описанной около этого треугольника.
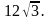Найдите радиус окружности, описанной около этого треугольника.
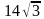. Найдите радиус окружности, описанной около этого треугольника.
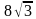. Найдите радиус окружности, вписанной в этот треугольник.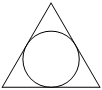
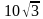. Найдите радиус окружности, вписанной в этот треугольник.
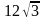. Найдите радиус окружности, вписанной в этот треугольник.
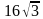. Найдите радиус окружности, вписанной в этот треугольник.
