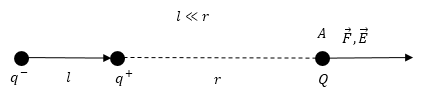Вектор электрического момента диполя (4 видео)

3.2. Электрический диполь

Чтобы понять механизм поведения диэлектриков в поле на микроскопическом уровне, нам надо сначала объяснить, как может электрически нейтральная система реагировать на внешнее электрическое поле. Простейший случай — полное отсутствие зарядов — нас не интересует. Мы знаем наверняка, что в диэлектрике имеются электрические заряды — в составе атомов, молекул, ионов кристаллической решетки и т. д. Поэтому мы рассмотрим следующую по простоте конструкции электронейтральную систему — два равных по величине и противоположных по знаку точечных заряда +q и –q, находящихся на расстоянии l друг от друга. Такая система называется электрическим диполем.

Электрический диполь — это система, состоящая из двух точечных равных по величине и противоположных по знаку зарядов, находящихся на расстоянии l друг от друга (рис. 3.6).

Рис. 3.6. Электрический диполь

Линии напряженности электрического поля и эквипотенциальные поверхности электрического диполя выглядят следующим образом (рис. 3.7, 3.8, 3.9)

Рис. 3.7. Линии напряженности электрического поля электрического диполя

Рис. 3.8. Эквипотенциальные поверхности электрического диполя

Рис. 3.9. Линии напряженности электрического поля и эквипотенциальные поверхности

Основной характеристикой диполя является электрический дипольный момент. Введем вектор l, направленный от отрицательного заряда (–q) к положительному (+q), тогда вектор р, называемый электрическим моментом диполя или просто дипольным моментом, определяется как

Рассмотрим поведение «жесткого» диполя — то есть расстояние которого не меняется — во внешнем поле Е (рис. 3.10).

Рис. 3.10. Силы, действующие на электрический диполь, помещенный во внешнее поле

Пусть направление дипольного момента составляет с вектором Е угол . На положительный заряд диполя действует сила, совпадающая по направлению с Е и равная F₁ = +qE, а на отрицательный — противоположно направленная и равная F₂ = –qE. Вращающий момент этой пары сил равен

Так как ql = р, то М = рЕ sin или в векторных обозначениях

(Напомним, что символ

означает векторное произведение векторов а и b.) Таким образом, при неизменном дипольном моменте молекулы () механический момент, действующий на нее, пропорционален напряженности Е внешнего электрического поля и зависит от угла между векторами р и E.

Под действием момента сил М диполь поворачивается, при этом совершается работа

которая идет на увеличение его потенциальной энергии. Отсюда получаем потенциальную энергию диполя в электрическом поле

если положить const = 0.

Из рисунка видно, что внешнее электрическое поле стремится повернуть диполь таким образом, чтобы вектор его электрического момента р совпал по направлению с вектором Е. В этом случае , а, следовательно, и М = 0. С другой стороны, при потенциальная энергия диполя во внешнем поле принимает минимальное значение , что соответствует положению устойчивого равновесия. При отклонении диполя от этого положения снова возникает механический момент, который возвращает диполь в первоначальное положение. Другое положение равновесия, когда дипольный момент направлен против поля является неустойчивым. Потенциальная энергия в этом случае принимает максимальное значение и при небольших отклонениях от такого положения возникающие силы не возвращают диполь назад, а еще больше отклоняют его.

На рис. 3.11 показан опыт, иллюстрирующий возникновение момента электрических сил, действующих на диэлектрик в электрическом поле. На удлиненный диэлектрический образец, расположенный под некоторым углом к силовым линиям электростатического поля, действует момент сил, стремящийся развернуть этот образец вдоль поля. Диэлектрическая палочка, подвешенная за середину внутри плоского конденсатора, разворачивается перпендикулярно его пластинам после подачи на них высокого напряжения от электростатической машины. Появление вращающего момента обусловлено взаимодействием поляризовавшейся палочки с электрическим полем конденсатора.

Рис. 3.11. Момент электрических сил, действующих на диэлектрик в электрическом поле

В случае неоднородного поля на рассматриваемый диполь будет действовать еще и равнодействующая сила F_paвн, стремящаяся его сдвинуть. Мы рассмотрим здесь частный случай. Направим ось х вдоль поля Е. Пусть диполь под действием поля уже повернулся вдоль силовой линии, так что отрицательный заряд находится в точке с координатой x, а положительный заряд расположен в точке с координатой х + l. Представим себе, что величина напряженности поля зависит от координаты х. Тогда равнодействующая сила F_paвн равна

Такой же результат может быть получен из общего соотношения

где энергия П определена в (3.8). Если Е увеличивается с ростом x, то

и проекция равнодействующей силы положительна. Это значит, что она стремиться втянуть диполь в область, где напряженность поля больше. Этим объясняется известный эффект, когда нейтральные кусочки бумаги притягиваются к наэлектризованной расческе. В плоском конденсаторе с однородным полем они остались бы неподвижными.

Рассмотрим несколько опытов, иллюстрирующих возникновение силы, действующей на диэлектрик, помещенный в неоднородное электрическое поле.

На рис. 3.12 показано втягивание диэлектрика в пространство между обкладками плоского конденсатора. В неоднородном электростатическом поле на диэлектрик действуют силы, втягивающие его в область более сильного поля.

Рис. 3.12. Втягивание жидкого диэлектрика в плоский конденсатор

Это демонстрируется при помощи прозрачного сосуда, в который помещен плоский конденсатор, и налито некоторое количество жидкого диэлектрика — керосина (рис.3.13). Конденсатор присоединен к высоковольтному источнику питания — электростатической машине. При ее работе на нижнем краю конденсатора, в области неоднородного поля, на керосин действует сила, втягивающая его в пространство между пластинами. Поэтому уровень керосина внутри конденсатора устанавливается выше, чем снаружи. После выключения поля уровень керосина между пластинами падает до его уровня в сосуде.

Рис. 3.13. Втягивание керосина в пространство между обкладками плоского конденсатора

В реальных веществах нечасто встречаются диполи, образованные только двумя зарядами. Обычно мы имеем дело с более сложными системами. Но понятие электрического дипольного момента применимо и к системам со многими зарядами. В этом случае дипольный момент определяется как

где , — величина заряда с номером i и радиус-вектор, определяющий его местоположение, соответственно. В случае двух зарядов мы приходим к прежнему выражению

Пусть наша система зарядов электрически нейтральна. В ней есть положительные заряды, величины которых и местоположения мы обозначим индексом «+». Индексом «–» мы снабдим абсолютные величины отрицательных зарядов и их радиус-векторы. Тогда выражение (3.10) может быть записано в виде

В (3.11) в первом слагаемом суммирование ведется по всем положительным зарядам, а во втором — по всем отрицательным зарядам системы.

Электрическая нейтральность системы означает равенство полного положительного заряда и суммы абсолютных величин всех отрицательных зарядов

Введем теперь понятие «центр зарядов» — положительных R + и отрицательных R –

Выражения (3.13) аналогичны формулам для центра масс в механике, и потому мы назвали их центрами положительных и отрицательных зарядов, соответственно. С этими обозначениями и с учетом соотношения (3.12) мы записываем электрический дипольный момент (3.11) системы зарядов в виде

где l-вектор, проведенный из центра отрицательных зарядов в центр положительных зарядов. Смысл нашего упражнения заключается в демонстрации, что любую электрически нейтральную систему зарядов можно представить как некий эквивалентный диполь.

Дополнительная информация

Содержание

Электрический диполь
Что такое электрический диполь
Модуль вектора сопряженности
Вычисление момента сил
Электрический момент диполя молекулы
📽️ Видео

Видео:40. Электрический дипольСкачать

Электрический диполь

Вы будете перенаправлены на Автор24

Видео:Электростатика | электрический дипольСкачать

Что такое электрический диполь

Электрическим диполем называется система из двух точечных зарядов, величина которых одинакова, но противоположна по знаку, при чем, эти точечные заряды разнесены на небольшое расстояние друг от друга. Вектор, соединяющий отрицательный заряд с положительным (направление от минуса к плюсу), называется плечом диполя.

Тогда векторная величина, равная:

называется моментом диполя (электрическим моментом диполя). В формуле (1) $q$ — абсолютное значение каждого из зарядов диполя.

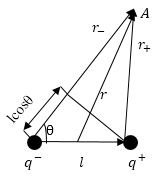
Электрическое поле диполя складывается из напряжённостей зарядов, которые составляют диполь. Так как плечо диполя мало, поэтому можно считать, что оно много меньше, чем расстояние до точек, в которых рассчитывается напряженность поля. Найдем потенциал диполя. В точке А (рис.1) формула для потенциала будет иметь вид:

Так как $lll r$, можно считать, что:

[r_—r_+approx lcostheta , r_-cdot r_+approx r^2left(3right).]

При этом местоположение точки A можно характеризовать вектором$overrightarrow$ с началом в любой точке диполя, ввиду малых геометрических размеров диполя. В таком случае формулу (2) можно записать в виде:

где $qlcostheta =frac<overrightarrow

cdot overrightarrow>.$ Зная связь напряженности поля и потенциала:

запишем формулу для напряженности поля диполя, которая будет иметь вид:

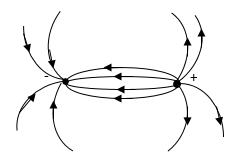
Согласно формуле (6) напряженность поля диполя убывает быстрее, чем напряженность кулоновского поля одиночного заряда, пропорционально третьей степени расстояния. Силовые линии электростатического поля около диполя изображены на рис. 2.

Видео:Лекция 3-1 Электрический дипольСкачать

Модуль вектора сопряженности

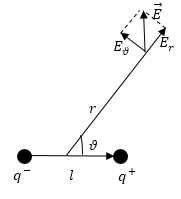
Если сферическую систему координат разместить так, чтобы ее центр совпал с серединой плеча диполя, а полярная ось была параллельна $overrightarrow

$ (рис.3), то составляющие вектора напряженности будут иметь вид:

В таком случае модуль вектора напряженности равен:

Видео:44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать

Вычисление момента сил

В однородном поле сила, которая действует на диполь со стороны поля ($overrightarrow$), равна нулю, так как к зарядам приложены одинаковые по модулю и противоположные по направлению силы:

где $<overrightarrow>_+$- сила, действующая на положительный заряд диполя, $<overrightarrow>$ — сила, действующая на отрицательный заряд диполя.

Момент этих сил равен:

Момент сил $overrightarrow$ стремится повернуть ось диполя в направлении поля $overrightarrow.$ Существует два положения равновесия диполя: диполь параллелен полю (устойчивое положение) и антипараллелен (неустойчивое положение).

Если поле не однородно, то сила (сумма сил действующих на положительный и отрицательный заряд) не равна нулю.$ overrightarrow=<overrightarrow>_++<overrightarrow>_-ne 0$. В этом случае сила равна:

В том случае, если мы имеем дело с точечным диполем (плечо диполя очень мало), то сила, действующая на диполь, может быть записана как:

или, что то же самое, но короче:

Задание: Ответьте на вопрос: может ли точечный заряд двигаться с постоянной скоростью вокруг неподвижного точечного диполя?

Ответ: Может, причем, расстояние заряда от диполя может быть любым. Плоскость круговой орбиты движения точечного заряда будет перпендикулярна оси диполя. Угол между направлением дипольного момента ($theta $) и радиус — вектором, который проведен к точечному заряду определяется выражением: cos ($theta $)=$pm sqrt$. Минус относится к положительному заряду.

Задание: Чему равна сила взаимодействия точечного заряда и точечного диполя? Дипольный момент диполя равен $p_e$. Расстояние между зарядом и диполем равно r, дипольный момент направлен вдоль соединяющей их прямой (рис.4).

Напряженность поля, которое создает диполь в точке А (где помещен заряд q) равна:

где $r_2$ — расстояние от точки А до положительного конца диполя, $r_1$ — расстояние до отрицательного конца, но мы считаем диполь точечный (плечо диполя много меньше чем расстояние до точки А ($lll r$)), тогда можно (2.1) преобразовать в:

Тогда силу с которой поле диполя действует на заряд, который помещен в точку А найдем как:

[F=Qcdot E left(2.3right).]

В результате получаем:

Ответ: Сила взаимодействия точечного заряда и точечного диполя равна $F=Qfrac.$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 03 12 2022

Видео:3. Поле диполя Электростатика и магнитостатикаСкачать

Электрический момент диполя молекулы

Электрический диполь — это физическая система из двух равных по величине и противоположных по знаку зарядов 5 (полюсов диполя), расположенных на расстоянии / друг от друга. Прямая линия, проходящая через по-

1 Подробнее о взаимосвязи структуры химических связей с геометрией молекул можно познакомиться по учебнику [14, с. 119—128].

люса диполя, называется осью диполя. Диполь характеризуется электрическим дипольным моментом р = 8 • /.

Дипольный момент является вектором, направленным от отрицательного полюса диполя к положительному. При наложении на диполь внешнего электрического поля его ось, совпадающая но направлению с вектором дипольного момента, ориентируется по направлению поля. При сближении диполя с другим зарядом или диполем возникают силы электростатического взаимодействия. Такие процессы часто протекают при образовании ковалентных полярных и ионных химических связей. Дипольный момент характеризует силу взаимодействия диполя с внешним электрическим нолем, а также силу взаимодействия диполя с другими электрическими зарядами и диполями.

Рис. 23. Схема дипольных моментов молекулы воды но модели МВС

Рассмотрим структуру молекулы водяного пара с учетом возникающего при ее образовании распределения зарядов внутри молекулы. Электроотрицательность кислорода по Полингу — 3,5, а водорода —

2,1. Следовательно, каждая из связей будет полярной, причем заряд 8- будет на кислороде, а 8+ — на водороде, т.е. образуются три центра электрического заряда и в молекуле образуются два электрических диполя. Схема дипольных моментов молекулы воды но модели МВС представлена на рис. 2.3.

В молекуле воды образуются два дипольных момента связей и р₂, которые при сложении дают общий дипольный момент молекулы р(Н₉0).

Важно подчеркнуть, что дипольные моменты связей складываются век- торно и суммарный дипольный момент зависит от геометрии молекулы. Таким образом, из-за того что в данном случае связи на схеме направлены иод прямым углом друг к другу, молекула в целом оказывается полярной. И эксперимент подтверждает это — дипольный момент молекулы воды равен 1,84 Д (1 Д (Дебай) равен 0,33- 10″ 29 Кл*м).

Теперь можно уточнить наше описание структуры молекулы воды в парообразном состоянии. Диполи, образовавшиеся в составе молекулы Н₂0, взаимодействуют друг с другом. Отрицательные полюса обоих диполей расположены на атоме кислорода. Электростатическое отталкивание положительных полюсов приводит к увеличению валентного угла. Этот вывод подтверждается экспериментально — измеренный валентный угол в молекуле водяного пара равен не 90°, как в рассмотренном выше простейшем варианте МВС, а 104,5°.