Задачи с радиус вектором (7 видео) | Курс школьной геометрии

К.Р. Радиус -вектор

Содержание

Просмотр содержимого документа «К.Р. Радиус -вектор»
Примеры решения задач с векторами
Координаты вектора
Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.
Траектория движения материальной точки через радиус-вектор
Вектор скорости материальной точки
Пример нахождения вектора скорости
Как найти вектор ускорения материальной точки
Модуль вектора скорости точки
Модуль вектора ускорения
Еще примеры решений задачи нахождения вектора скорости и ускорения
🎦 Видео

Просмотр содержимого документа
«К.Р. Радиус -вектор»

Способы задания положения материальной точки в пространстве

Радиус-вектор, проведенный к начальной точке, имеет координаты (2;3). Найти длину радиус-вектора.

Тело переместилось из точки с координатами (5;4) в точку (10;-3). Во сколько раз по длине отличаются эти векторы.

Сначала тело переместилось в точку с координатами (-1;15), а затем — в точку с координатами (3;7). Определить результирующий радиус-вектор.

За какое время тело прошло дистанцию, если его средняя скорость 60 км/ч, а радиус-вектор, проведенный к конечной точки движения, имеет координаты (30;5). За начало движения принять точку с координатами (0;0).

Способы задания положения материальной точки в пространстве

Радиус-вектор, проведенный к начальной точке, имеет координаты (6;3). Найти длину радиус-вектора.

Тело переместилось из точки с координатами (-5;4) в точку (10;3). Во сколько раз по длине отличаются эти векторы.

Сначала тело переместилось в точку с координатами (1;-15), а затем — в точку с координатами (3;7). Определить результирующий радиус-вектор.

За какое время тело прошло дистанцию, если его средняя скорость 20 км/ч, а радиус-вектор, проведенный к конечной точки движения, имеет координаты (30;-5). За начало движения принять точку с координатами (0;0).

Способы задания положения материальной точки в пространстве

Радиус-вектор, проведенный к начальной точке, имеет координаты (2;3). Найти длину радиус-вектора.

Тело переместилось из точки с координатами (5;4) в точку (10;-3). Во сколько раз по длине отличаются эти векторы.

Способы задания положения материальной точки в пространстве

Радиус-вектор, проведенный к начальной точке, имеет координаты (6;3). Найти длину радиус-вектора.

Тело переместилось из точки с координатами (-5;4) в точку (10;3). Во сколько раз по длине отличаются эти векторы.

Видео:Определение параметров движения по заданному радиус-вектору. Векторный способ задания движения.Скачать

Примеры решения задач с векторами

Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других прикладных науках. На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними.

Перед изучением примеров решения задач советуем изучить теоретический материал по векторам, прочитать все определения и свойства. Список тем находится в правом меню.

Координаты вектора

Теоретический материал по теме — координаты вектора.

Видео:10 Класс - Физика - Перемещение. Радиус-вектор.Скачать

Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.

В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.

Видео:Радиус векторСкачать

Траектория движения материальной точки через радиус-вектор

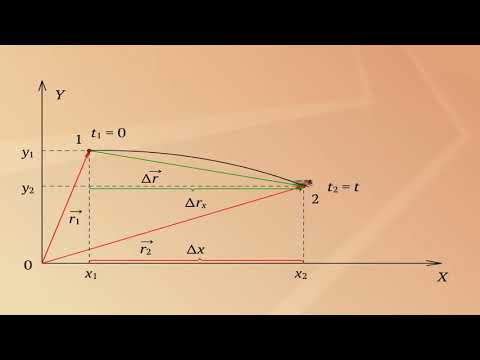
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Видео:Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Видео:Радиус-векторыСкачать

Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Видео:Лекция 4. ВЕКТОРА │ кинематика с нуляСкачать

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Видео:2.4. Радиус-вектор и вектор перемещенияСкачать

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.