Здравствуйте! Сегодня разберём олимпиадную задачу по информатике, которая называется треугольные числа.
Задача треугольные числа.
Школьник Никита этим летом отдыхал со своими родителями. Его любимым занятием на пляже было складывать из камешков правильные треугольники (правильным называется треугольник, у которого все стороны равны). Никита и не предполагал, что числа, из которых можно сложить правильный треугольник, называются треугольными. Вот несколько треугольных чисел: 1, 3, 6, 10, … .
Помогите Никите по заданному количеству камешков N найти наибольшую сторону правильного треугольника, который из них можно сложить. Например, если у Никиты 30 камешков, то длина наибольшей стороны правильного треугольника, который из них можно сложить, будет 7.

Тесты для самопроверки:
| 30 | 7 |
| 29 | 7 |
| 28 | 7 |
| 27 | 6 |
| 9876543210000 | 4444443 |
| 9223372036854775807 | 4294967295 |
Рассмотрим треугольные числа. Видим, что первое треугольное число — это просто 1. Второе число — это сумма чисел до 2 (1+2), третье число — сумма чисел до 3 (1+2+3) и т.д.
Плюс ко всему, второе число образует треугольник со стороной 2, третье число со стороной 3 и т.д.
Рассмотрим треугольное число по номером n. Видим, что это сумма арифметической прогрессии.
Свернём по формуле арифметической прогрессии. Число Sn (сумма арифметической прогрессии) в нашей задаче это количество камней, которое вводит пользователь. Число n в данном уравнении обозначает порядковый номер треугольного числа или длину стороны правильного треугольника, который можно составить из данного количества камней.
Остаётся решить данное уравнение относительно n в целых числах, чтобы разгадать нашу задачу.
Последние уравнение это и есть ответ в нашей задаче. Если n — будет дробным, значит мы должны его округлить в меньшую сторону, т.к. наше уравнение решается только в целых числах. (Дробное количество камней не может быть).
Запрограммируем данную задачу на C#
Т.к. число 9223372036854775807 * 8 превышает максимальное число даже для типа ulong, то будем использовать специальный тип BigInteger.
Для того, чтобы использовать BigInteger, нужно в ссылках добавить System.Numerics . И прописать using System.Numerics в программе.
Для этого типа данных не работает стандартная функция извлечения корня Math.Sqrt(), поэтому мы напишем свою функцию извлечения корня основанную на методе Ньютона. Эта функция извлекает корень и округляет результат в меньшую сторону. Об этом методе можете прочитать подробно в статье на этом сайте.
На этом всё, до свидания!
Видео:МАТЕМАТИЧЕСКИЕ ЗАГАДКИ .СТРАННАЯ МАТЕМАТИКА.ФЕНОМЕН ТРЕУГОЛЬНИКА.Скачать

Вариации на тему «Треугольник Паскаля»
Вариации на тему «Треугольник Паскаля»
Треугольник Паскаля является, пожалуй, одной из наиболее известных и изящных числовых схем во всей математике.
Блез Паскаль, французский математик и философ, посвятил ей специальный «Трактат об арифметическом треугольнике».
Впрочем, эта треугольная таблица была известна задолго до 1665 года — даты выхода в свет трактата.
Так, в 1529 году треугольник Паскаля был воспроизведен на титульном листе учебника арифметики, написанного астрономом Петром Апианом.
Изображен треугольник и на иллюстрации книги «Яшмовое зеркало четырех элементов» китайского математика Чжу Шицзе, выпущенной в 1303 году.
Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника в 1110 году, в свою очередь заимствовав его из более ранних китайских или индийских источников.
Построение треугольника Паскаля
Треугольник Паскаля — это просто бесконечная числовая таблица «треугольной формы», в которой на вершине и по боковым сторонам стоят единицы, каждое из остальных чисел равно сумме двух чисел, стоящих над ним слева и справа в предшествующей строке. Таблица обладает симметрией относительно оси, проходящей через его вершину.
Свойства треугольника Паскаля
- Сумма чисел n-й строки Паскаля равна 2 n (потому что при переходе от каждой строки к следующей сумма членов удваивается, а для нулевой строки она равна 20=1) Все строки Паскаля симметричны (потому что при переходе от каждой строки к следующей свойство симметричности сохраняется, а нулевая строка симметрична) Каждый член строки Паскаля с номером n тогда и только тогда делится на т, когда т — простое число, а n — степень этого простого числа
Треугольные числа
Вдоль диагоналей, параллельных сторонам треугольника, выстроены треугольные, тетраэдрические и другие числа. Треугольные числа указывают количество шаров или других предметов, уложенных в виде треугольника (эти числа образуют следующую последовательность: 1,3,6,10,15,21. в которой 1- первое треугольное число, 3- второе треугольное число, 6-третье и т. д. до m-ro, которое показывает, сколько членов треугольника Паскаля содержится в первых m его строках — от нулевой до (m-1)-й).
Тетраэдрические числа
Члены последовательности 1,4, 10, 20, 36, 56. называются пирамидальными, или, более точно, тетраэдрическими числами: 1- первое тетраэдрическое число, 4- второе, 10- третье и т. д. до m-ro. Эти числа показывают, сколько шаров может быть уложено в виде треугольной пирамиды (тетраэдра).
Числа Фибоначчи
В 1228 году выдающийся итальянский математик Леонардо из Пизы, более известный сейчас под именем Фибоначчи, написал свою знаменитую «Книгу об абаке». Одна из задач этой книги — задача о размножении кроликов — приводила к последовательности чисел 1,1,2,3,5,8,13,21. в которой каждый член, начиная с третьего, представляет собой сумму двух предыдущих членов. Эта последовательность носит название ряда Фибоначчи, члены ряда Фибоначчи называют числами Фибоначчи. Обозначая n-е число Фибоначчи через
Между рядом Фибоначчи и треугольником Паскаля существует любопытная связь. Образуем для каждой восходящей диагонали треугольника Паскаля сумму всех стоящих на этой диагонали чисел. Получим для первой диагонали 1, для второй 1, для третьей 2, для четвертой 3, для пятой 5. Мы получили не что иное, как пять начальных чисел Фибоначчи. Оказывается, что всегда сумма чисел n-й диагонали есть n-е число Фибоначчи. Для доказательства интересующего нас предложения достаточно показать, что сумма всех чисел, составляющих n-ю и (n+1) диоганали треугольника Паскаля равна сумме чисел, составляющих его т+2-ю диагональ.
Биномиальные коэффициенты
Числа, стоящие по горизонтальным строкам, являются биномиальными коэффициентами. Строка с номером n состоит из коэффициентов разложения бинома (1+n)n. Покажем это при помощи операции Паскаля. Но сначала представим, как биномиальные коэффициенты определяются.
Возьмем бином 1+х и начнем возводить его в степени 0, 1, 2, 3 и т. д., располагая получающиеся при этом многочлены по возрастающим степеням буквы х. Мы получим
Вообще, для любого целого неотрицательного числа n
(1+x)n=a0+a1x+a2x2+. +apxp,
где a0,a1. ap
Последнее соотношение можно переписать в виде а из соотношений 1-4 получаем
Образовался треугольник Паскаля, каждый элемент которого
Именно это фундаментальное свойство треугольника Паскаля связывает его не только с комбинаторикой и теорией вероятностей, но и с другими областями математики и ее приложений.
Решение задач с применением треугольника Паскаля
Старинные задачи о случайном
Еще в глубокой древности появились различные азартные игры. В Древней Греции и Риме широкое распространение получили игры в астрагалы, когда игроки бросали кости животных. Также пользовались популярностью игральные кости — кубики с нанесенными на гранях точками. Позднее азартные игры распространились в средневековой Европе.
Эти игры подарили математикам массу интересных задач, которые потом легли в основу теории вероятностей. Очень популярны были задачи о дележе ставки. Ведь, как правило, игра велась на деньги: игроки делали ставки, а победитель забирал всю сумму. Однако игра иногда прерывалась раньше финала, и возникал вопрос: как разделить деньги.
Многие математики занимались решением этой проблемы, но до середины XVII века так и не нашли его. В 1654 году между французскими математиками Блезом Паскалем, уже хорошо известным нам, и Пьером Ферма возникла переписка по поводу ряда комбинаторных задач, в том числе и задач о дележе ставки. Оба ученых, хотя и несколько разными путями, пришли к верному решению, деля ставку пропорционально вероятности выигрыша всей суммы при продолжении игры.
Следует отметить, что до них никто из математиков вероятность событий не вычислял, в их переписке теория вероятностей и комбинаторика впервые были научно обоснованы, и поэтому Паскаль и Ферма считаются основателями теории вероятностей.
Рассмотрим одну из задач Ферма, решенную Паскалем с помощью своей числовой таблицы.
Пусть до выигрыша всей встречи игроку А недостает двух партий, а игроку В — трех партий. Как справедливо разделить ставку, если игра прервана?
Паскаль складывает количество партий, недостающих игрокам, и берет строку таблицы, в которой количество членов равно найденной сумме, т. е. 5. Тогда доля игрока А будет равна сумме трех (по количеству партий, недостающих игроку В) первых членов пятой строки, а доля игрока В — сумме оставшихся двух чисел. Выпишем эту строку: 1,4,6,4, 1. Доля игрока А равна 1+4+6=11, а доля В -1+4=5.
Другие арифметические треугольники
Рассмотрим треугольники, построение которых связано с известными однопараметрическими комбинаторными числами. Создание таких треугольников основано на принципе построения рассматриваемого выше треугольника Паскаля.
Рассмотрим построенный арифметический треугольник. Данный треугольник носит название треугольника Люка, так как суммы чисел, стоящих на восходящих диагоналях, дают последовательность чисел Люка: 1, 3, 4, 7, 11, 18, / которые могут быть определены как
Ln=Ln-1+Ln-2, L0=2, L1=1
Каждый элемент треугольника определяется по правилу Паскаля Ln+1,k=Ln, k-1+Ln, k при начальных условиях L1,0=1, L1,1=2 и L0,k=0
т. е. n-я строка треугольника люка может быть получена сложением n-й и (n-1)-й строк треугольника Паскаля.
Из чисел (fm, n), удовлетворяющих уравнениям
fm, n=fm-1,n+fm-2,n,
fm, n=fm-1,n-1+fm-2,n-2, где с начальными условиями f0,0=f1,0=f1,1=f2,1=1 строится следующий треугольник.
fm, n =fn fn-m, m Є n Є 0, где fn — n — е число Фибоначчи. Построенный треугольник назван треугольником Фибоначчи.
Рассмотрим еще один треугольник, создание которого основано на методе построения треугольника Паскаля. Это треугольник Трибоначчи. Он назван так потому, что суммы элементов, стоящих на восходящих диагоналях, образуют последовательность чисел Трибоначчи: 1,1,2,4,7,13,24,44. которая может быть определена следующим рекуррентным соотношением: tn+3 = tn+2 + tn+1 + tn с начальными условиями t0 = 1, t1 = 1, t2 = 2
Построение «знакового треугольника»
Перед нами треугольник, составленный из одних знаков, плюсов и минусов, по принципу образования треугольника Паскаля. В отличие от последнего, он расположен основанием вверх.
Сначала задается первая строка, состоящая из произвольного количества знаков и их расположения. Каждый знак следующей строки получается путем перемножения двух вышестоящих знаков.
Одной из наших задач является установить, при каком количестве знаков первой строки число минусов и плюсов будет одинаковым. Общее количество знаков в таблице можно определить формулой
где n — число знаков в первой строке.
Образуется последовательность чисел, при которых количество минусов и плюсов может быть равным: 3, 4, 7, 8, 11, 12, 15, 16. каждое из которых показывает количество знаков в первой строке. Однако не установлено, при каком расположении знаков число минусов и плюсов будет однозначно одинаковым.
Второй нашей задачей, касающейся треугольника произведения знаков, является установление наименьшего количества плюсов, которое может иметь «знаковый треугольник».
Существует интересная последовательность знаков первой строки: +, -, -, +, -, -, . (или -, -, + ,- ,- ,+ , . ), при которой число плюсов, как до сих пор считается, будет наименьшим и равным 1/3 от общего числа знаков, т. е. равным
Важно заметить, что если постепенно обходить треугольник, то последовательность знаков +, -, -, . сохранится.
Обратим внимание на тот факт, что наименьшее количество плюсов, равное 1/3 от общего числа знаков, можно увидеть и в треугольнике при n = 2.
Видео:Задача, которую исключили из экзамена в АмерикеСкачать

Треугольник Паскаля, работа учащейся 9 класса, представленная на сессию МАН, занявшая первое место
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Министерство образования и науки, молодежи и спорта
Автономной Республики Крым
МАЛАЯ АКАДЕМИЯ НАУК ШКОЛЬНИКОВ КРЫМА «ИСКАТЕЛЬ»
Удивительный треугольник Паскаля и его загадочные свойства
Работу выполнила: Костенко Елизавета
МБОУ «Гвардейская школа-гимназия №2» 9 кл.)
Научный руководитель: Исаева Н. Н.,
Учитель высшей категории, учитель математики
МБОУ «Гвардейской школы-гимназии №2»
Симферопольский район — 2016 г.
Костенко Елизавета Александровна
Ученица 9 класса МБОУ «Гвардейской школы-гимназии №2»
Исаева Нина Николаевна
Учитель высшей категории, учитель математики МБОУ «Гвардейской школы-гимназии №2»
Тема работы: Удивительный треугольник Паскаля и его загадочные свойства
Цель: ознакомиться с треугольником Паскаля как с разновидностью треугольников, изучить свойства арифметического треугольника, рассмотреть применение треугольника в разных сферах жизни, узнать более обширную и подробную информацию о числовой таблице, а также выявить связь треугольника Паскаля с числами Фибоначчи и биномиальными коэффициентами.
Задачи: изучить литературу по теме «Треугольник Паскаля», выявить свойства чисел, входящих в состав арифметического треугольника, определить применение свойств чисел треугольника Паскаля, сформулировать вывод и итоги исследования.
Актуальность данной работы обусловлена широким интересом к теме «Треугольник Паскаля» в современной науке, а также ее недостаточной разработанностью. Данная работа позволяет выявить, насколько широко применяются треугольники в практической жизни, и какую они играют роль в различных направлениях.
Предмет исследования: свойства треугольника Паскаля.
Мой личный вклад в работу состоит в отслеживании свойств арифметического треугольника в школьных учебниках, материалах ГИА и ЕГЭ, а также дополнительной литературе.
Практическое значение работы: материалы данной работы могут быть использованы в качестве дополнительного материала на уроках алгебры и геометрии как в обычных, так и в профильных классах.
Выводы: таким образом, я познакомилась с треугольником Паскаля как с разновидностью треугольников, изучила свойства арифметического треугольника, выяснила какая же связь существует между числами Фибоначчи и биномиальными коэффициентами, рассмотрела его применение в решении некоторых задач.
Блез Паскаль – французский математик…………………………………….7
Треугольник Паскаля как разновидность треугольников…………………8
Свойства арифметического треугольника ………………………………. 12
Исследование теории вероятности и последовательности чисел Фибоначчи. Биномиальные коэффициенты. Примеры решения задач с использованием свойств арифметического треугольника
2.1. Связь треугольника Паскаля с теорией вероятности………………………15
2.2. Закономерности в последовательности ряда чисел Фибоначчи…………..17
2.3. Биномиальные коэффициенты и их применение в различных областях математики…………………………………………………………………………. 18
Методы решения задач по теме «Треугольник Паскаля»
3.1. Составление последовательности тренировочных задач по теме «Треугольник Паскаля» ………………………………………………………………………………………..21
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ……………………..………23
Тема моей работы звучит так: «Удивительный треугольник Паскаля».
Объектом исследования является треугольник Паскаля как таблица коэффициентов.
Предметом исследования являются свойства треугольника Паскаля.
Целью работы является ознакомление с треугольником Паскаля как с разновидностью треугольников, изучение свойств треугольника Паскаля, рассмотрение применения арифметического треугольника в разных сферах жизни, выявление связи треугольника с биномиальными коэффициентами и числами Фибоначчи.
Актуальность данной работы обусловлена широким интересом к теме «Треугольник Паскаля» в современной науке, а также ее недостаточной разработанностью. Данная работа позволяем выявить насколько широко применяется арифметический треугольник в математике.
Задачами исследования является изучение литературы по теме «Треугольник Паскаля», выявление свойств чисел, входящих в состав арифметического треугольника, определение применения свойств чисел треугольника Паскаля, формулирование вывода и подведение итогов исследования.
Для достижения поставленной цели и задач необходимо решить следующие задачи:
Изучить статьи и учебно-методическую литературу по данной теме.
Проанализировать действующие учебники, содержащие материалы по данной теме.
Рассмотреть основные методы и приемы решения задач по теме «Треугольник Паскаля» .
Два года назад произошло наше увлекательное знакомство с таинственным и загадочным миром геометрии. Одной из глав курса геометрии 7 класса называется «Треугольники». Меня очень заинтересовала данная тема. Я всегда хотела узнать много нового о треугольниках. Ведь мир треугольников очень удивителен и интересен. Я хочу узнать как можно больше о происхождении треугольников, об их значении в нашей жизни.
Треугольник — первая геометрическая фигура, встречающаяся в древних орнаментах. Изучая литературу, я узнала, что у разных народов и в разные времена он служил для воплощения возвышенных образов природы и природных сил в простые и загадочные символы. Например, в Египте он символизировал триаду духовной воли, любви, интуиции и высшего разума человека, то есть его личность или душу. Треугольник с горизонтальной чертой считается пассивным и означает воздух, умеренный огонь, соответствующий синему цвету. Перевернутый треугольник означает чашу, готовую принять воду; мудрость, порождающую главную идею; зеленый цвет. Треугольник воздуха с горизонтальной чертой символизирует Землю, неподвижную стоячую воду и соответствует черному цвету. Ацтеки использовали изображение треугольника с вершиной наверху, соединенного с перевернутым треугольником, в качестве символа временного цикла. Треугольник в сочетании с крестом образует алхимический знак Серы. Равносторонний треугольник, символизирующий, по древнееврейской традиции, совершенство, у христиан означает Троицу — Отца, Сына и Святого Духа.
Когда я подробно познакомилась с треугольником Паскаля, большим открытием для меня оказалось, что это и не совсем треугольник в привычном для нас представлении. Это скорее таблица с интересной структурой, простой и совершенной, содержащая числа – коэффициенты. Поскольку числа данного треугольника обладают особыми свойствами, то сам треугольник Паскаля можно считать универсальным математическим инструментом. Именно это и является гипотезой моего исследования.
Блез Паскаль – французский математик
Блез Паскаль (19 июня 1623, Клермон-Ферран, — 19 августа 1662, Париж) — французский математик, физик, литератор, философ, один из основателей математического анализа, теории вероятностей и проективной материи. Паскаль был первоклассным математиком. Он помог создать два крупных новых направления математических исследований. Его удобное представление биномиальных коэффициентов в виде таблицы, изложенное в «Трактате об арифметике треугольника», увидевшем свет в 1653 г., (на тот момент Блезу Паскалю было шестнадцать лет ), получит название «треугольника Паскаля». Кроме того, Паскаль открыл и исследовал алгебраическую кривую, с тех пор получившую название «улитка Паскаля». Переписка французского математика с Пьером де Ферма по теории вероятностей впоследствии оказало принципиальное влияние на развитие современной экономики.
Треугольник Паскаля как разновидность треугольников
Изучая литературу, я выяснила, что треугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами и назван в честь великого французского математика Блеза Паскаля. В действительности, треугольник Паскаля был известен задолго до 1653 года, что является датой выхода «Трактата об арифметическом треугольнике». Так, этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета. Изображен такой треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника около 1100 года, в свою очередь, заимствовав его из более ранних китайских или индийских источников.
Из книги «Математические новеллы» (М., Мир, 1974) Мартина Гарднера я хотела бы привести его высказывание: «Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике»
Я рассмотрела схему построения треугольника, предложенную Гуго Штейнгаузом в его классическом «Математическом калейдоскопе»: предположим, что вы входите в город как показано на схеме синей стрелкой, и можете двигаться только вперед, точнее, все время выбирая, вперед налево, или вперед направо. Узлы, в которые можно попасть только единственным образом, отмечены зелеными смайликами, точка, в которую можно попасть двумя способами, показана красным смайликом, а тремя, соответственно — розовыми. Это один из вариантов построения треугольника.
Свойства арифметического треугольника
🔥 Видео
Решали пол-урока, а оказалось очень простоСкачать

Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

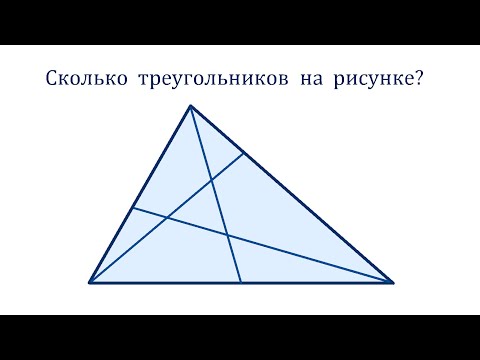
Сколько треугольников на рисунке? Универсальный алгоритм решения задачиСкачать
Треугольники. Практическая часть - решение задачи. 7 класс.Скачать

Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Задача про соотношение сторон. Геометрия 7 класс.Скачать

Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

Переставь одну цифру! Задача на логикуСкачать

Треугольник ПаскаляСкачать

Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Задача, которой русские школьники мучали американскихСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Задача, которую боятсяСкачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Найдите угол: задача по геометрииСкачать

Найти площадь треугольника АВС. Задачи по рисункамСкачать





















