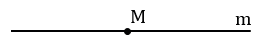Построить параллельные прямые и перпендикуляр к прямой (5 видео)

Построение перпендикулярных прямых

Примеры:

1. Даны прямая и точка на ней. Построить прямую проходящую через данную точку и перпендикулярную к данной прямой.

Дано: прямая m, Mm.

Построить: МPm.

Решение:

Произвольно строим с помощью линейки прямую m и отмечаем на ней точку М.

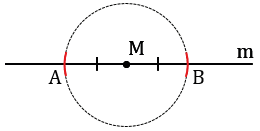
На лучах прямой m, исходящих из точки М, с помощью циркуля откладываем равные отрезки МА и МВ (МА = МВ). Для этого строим окружность с центром в точке М, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки М (смотри выделенное красным).

Затем строим две окружности с центрами в точках А и В радиуса АВ (полностью окружности строить необязательно, смотри выделенное фиолетовым и красным цветом).

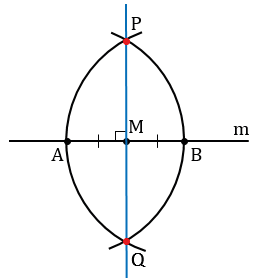
Данные окружности пересекаются в двух точках, обозначим их Р и Q. Проведем с помощью линейки через точку М и одну из точек Р или Q прямую, например, МР.

Докажем, что прямая МР — искомая прямая, т.е. что МPm.

Рассмотрим треугольник АРВ.

АР = ВР, т.к. по построению это радиусы одинаковых окружностей, следовательно, АРВ — равнобедренный. По построению МА = МВ, т.е. МР — медиана равнобедренного треугольника, тогда по свойству равнобедренного треугольника МР и высота, т.е. МPm. Что и требовалось доказать.

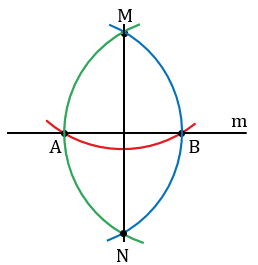
2. Даны прямая и точка не лежащая на этой прямой. Построить прямую проходящую через данную точку и перпендикулярную к данной прямой.

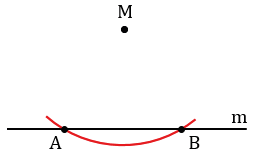
Дано: прямая m, Mm.

Построить: МNm.

Решение:

Произвольно строим с помощью линейки прямую m и отмечаем точку М, не лежащую на прямой m.

Далее строим окружность с центром в данной точке М, пересекающую прямую m в двух точках, которые обозначим буквами А и В (всю окружность строить необязательно, смотри выделенное красным цветом).

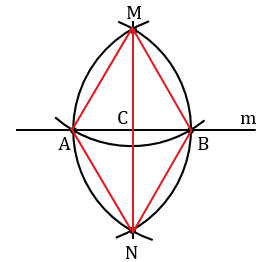
Затем построим две окружности с центрами в точках А и В, проходящие через точку М (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Эти окружности пересекутся в точке М и еще в одной точке, которую обозначим буквой N. Проведем прямую МN.

Докажем что, прямая МN — искомая, т.е. МNm.

В АМN и ВМN: АМ = АN = ВМ = ВN — радиусы, МN — общая, следовательно, АМN =ВМN (по трем сторонам), значит, углы ВМС и АМС равны (С точка пересечения прямых m и МN). Отсюда следует, что отрезок МС — биссектриса равнобедренного треугольника АМВ (АМ = ВМ — радиусы) с основанием АВ, тогда по свойству равнобедренного треугольника АМ — высота, значит, МNАВ, т.е. МNm.

Поделись с друзьями в социальных сетях:

Содержание

Геометрия. 7 класс
Прямая. Параллельные и перпендикулярные прямые.
теория по математике 📈 планиметрия
Обозначения прямой
Признаки параллельности прямых
Аксиома параллельных прямых
Следствия из аксиом параллельных прямых
Перпендикулярные прямые
🎬 Видео

Видео:Параллельные прямые. 6 класс.Скачать

Геометрия. 7 класс

Конспект урока

Параллельные и перпендикулярные прямые

Перечень рассматриваемых вопросов:

Взаимное расположение прямых на плоскости.
Параллельные прямые.
Аксиома параллельных прямых.
Перпендикулярные прямые.
Расстояние от точки до прямой, между параллельными прямыми.

Параллельные прямые – две прямые на плоскости называются параллельными, если они не пересекаются.

Перпендикулярные прямые – две прямые называются перпендикулярными, если при пересечении они образуют четыре прямых угла.

Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Взаимное расположение двух прямых на плоскости.

Вспомните, как могут располагаться на плоскости две прямые.

Две прямые на плоскости называются параллельными, если они не пересекаются.

Аксиома параллельных прямых: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Углы, изображенные на рисунке:

Накрест лежащие: 3 и 5; 4 и 6.

Соответственные: 1 и 5; 2 и 6; 3 и 8; 4 и 7.

Односторонние: 3 и 6; 4 и 5.

Признаки и свойства параллельных прямых.

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

Это признаки параллельности прямых. Обратные теоремы верны и представляют свойства параллельных прямых.

Способ построения параллельных прямых:

Аксиома параллельных прямых.

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Если две прямые параллельны третьей, то они параллельны.

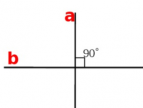
Если две прямые, пересекаясь, образуют четыре прямых угла, они называются перпендикулярными.

Прямые а и b на рисунке перпендикулярны: а ⏊ b.

Через каждую точку можно провести прямую, перпендикулярную данной и притом только одну.

Это можно сделать, пользуясь угольником или транспортиром.

Перпендикулярность и параллельность прямых.

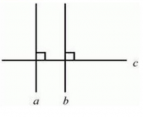
Две прямые, перпендикулярные к третьей не пересекаются т. е параллельны между собой.

Отрезок АВ, перпендикулярный к прямой а, называют перпендикуляром. Точка В – основание перпендикуляра.

Из любой точки, не лежащей на данной прямой, можно опустить перпендикуляр на эту прямую и притом только один.

Длину перпендикуляра АВ называют расстоянием от точки А до прямой а.

Расстоянием между параллельными прямыми называют расстояние АВ от любой точки одной прямой до другой прямой.

Разбор заданий тренировочного модуля.

Решение: ∠1 и ∠2 соответственные, по свойству параллельных прямых: ∠1 = ∠2 = 220°: 2 = 110°.
∠2 и ∠3 смежные, по свойству смежных углов: ∠2 + ∠3 = 180° значит, ∠3 = 180° – 110° = 70°.

№ 2. Докажите, что биссектрисы смежных углов перпендикулярны.

Пусть ∠АОВ и ∠ВОС – смежные углы. ОК и ОР – их биссектрисы.
∠KOP = ∠КОВ + ∠ВОР. Поскольку ОК и ОВ – биссектрисы, то ∠КОВ = 1/2∠АОВ, ∠ВОР = 1/2∠ВОС по определению биссектрисы.
Тогда ∠КОР = 1/2∠АОВ + 1/2∠ВОС = 1/2(∠АОВ + ∠ВОС) = 180° : 2 = 90°.
Итак, ОК ⏊ ОР т. е. прямые перпендикулярны.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Прямая. Параллельные и перпендикулярные прямые.

теория по математике 📈 планиметрия

Линия, которую изображают на плоскости при помощи линейки, причем, эта линия не должна быть ограничена точкой ни с одной стороны, называют прямой. Другими словами, прямая не имеет ни начала, ни конца.

Обозначения прямой

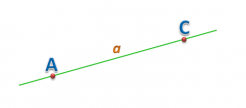
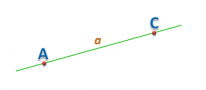
Обычно прямые обозначают прописной латинской буквой или двумя заглавными (если на прямой лежат точки). Рассмотрим это на рисунке. Данную прямую мы можем назвать двумя способами: прямая а; прямая АС.

Рассмотрим теперь две прямые на плоскости. Для них существует два случая расположения: пересекаются и не пересекаются.

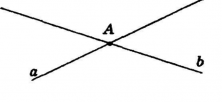
Если две прямые пересекаются, то есть имеют общую точку, то их называют пересекающимися. На рисунке показаны прямые а и b, которые пересекаются в точке A. Запись с помощью символов для данного рисунка выполняют следующим образом: а ∩ b=А, где ∩ — это знак «пересечение».

Если две прямые на плоскости не пересекаются, то их называют параллельными прямыми. На рисунке изображены параллельные прямые. Запись осуществляется следующим образом: a | | b, где | | — знак параллельности.

Признаки параллельности прямых

Рассмотрим прямую с, которая пересекает две прямые а и b и образует с ними восемь углов. Такую прямую с называют — секущая. Пары углов, которые образует секущая, также имеют названия. Итак, на данном рисунке изображены эти все прямые и восемь углов.

Необходимо запомнить названия следующих углов:

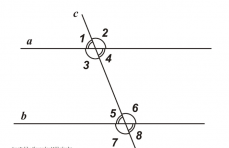
накрест лежащие углы: 4 и 5; 3 и 6;
односторонние углы: 4 и 6; 3 и 5;
соответственные углы: 1 и 5; 3 и 7; 2 и 6; 4 и 8.

С данными углами связаны следующие признаки параллельности прямых:

если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны;
если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны;
если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 180 0 , то прямые параллельны.

Видео:Перпендикулярные прямые. 6 класс.Скачать

Аксиома параллельных прямых

Вспомним, что аксиомой принято называть утверждения, не требующие доказательств.

Через любые две точки на плоскости проходит прямая и притом только одна.

Аксиома №2 Через точку, не лежащую на данной прямой, можно провести только одну прямую параллельную данной.

Видео:Перпендикулярные прямыеСкачать

Следствия из аксиом параллельных прямых

Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

На данном рисунке видно, что а и b параллельные прямые, с – секущая, она пересекает прямую а в точке А, значит и будет пересекать прямую b в некоторой точке С.

Если две прямые параллельны третьей, то они параллельны.

По данному рисунку видно, что если прямая CD параллельна АВ и прямая MN параллельна АВ, то CD и MN тоже будут параллельны.

Видео:6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Перпендикулярные прямые

Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.

На рисунке показаны такие прямые а и b. Запись с помощью символов можно сделать следующим образом: а ⊥ b, где « ⊥ » — знак перпендикулярности. Заметим, что две прямые, перпендикулярные к третьей, не пересекаются. На данном рисунке а ⟂ с, b ⟂ c. Видно, что прямые а и b не пересекаются, то есть они – параллельны.