Задачи на радиусы вписанных и описанных окружностей в правильные многоугольники (8 видео)

Урок геометрии по теме «Правильные многоугольники. Решение задач». 9-й класс

Разделы: Математика

Класс: 9

Основная цель:

Проверить уровень обязательной математической подготовки, глубину усвоения знаний и умений применять полученные знания в несколько отличных от обязательных результатов обучения ситуациях.

Тренировать способность к решению задач на нахождение длин сторон правильных многоугольников, периметров, длин окружностей.

Тренировать умение понимать текст задачи, делать чертежи, сопровождающие условие и решение задачи, выделять конфигурацию, необходимую на данном шаге (этапе) решения.

Проверка домашнего задания.

а) Индивидуальная работа у доски.

Построить правильный многоугольник: n=3, n=4, n=6.

б) Фронтальный опрос.

Задания для класса.

Видео:Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

Что такое многоугольник? Какой многоугольник называется выпуклым?

Какой многоугольник называется правильным?

Что называется углом выпуклого многоугольника при данной вершине?

Что является внешним углом выпуклого многоугольника при данной вершине?

Чему равна сумма углов выпуклого многоугольника?

Многоугольник называется вписанным в окружность, если :

Многоугольник называется описанным около окружности, если :

Правильный выпуклый многоугольник является вписанным и :

а) Заполните таблицу:

Число сторон многоугольника n	Выражение радиусов вписанной r_n и описанной R_n окружностей через сторону a_n многоугольника
n	R=	r=
3	R₃=	r₃=
4	R₄=	r₄=
6	R₆=	r₆=

б) Заполните таблицу:

Число сторон многоугольника n	Выражение стороны a_n многоугольника через радиусы вписанной r_n и описанной R_n окружностей
n	a_n=	a_n=
3	a₃=	a₃=
4	a₄=	a₄=
6	a₆=	a₆=

в) Устное решение задач(№ 1, 2, 3) по готовым чертежам.

Задача 1. Радиус окружности, вписанной в квадрат, равен 1 см. Найдите радиус R описанной окружности около этого квадрата. (Ответ: см)

Задача 2. Периметр правильного шестиугольника, описанного около окружности, равен см. Чему равен радиус этой окружности? (Ответ: 1,5 см)

Задача 3. Периметр квадрата, вписанного в окружность, равен см. Найдите радиус r вписанной окружности. (Ответ: см)

Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Геометрический диктант.

Какие четырехугольники являются правильными многоугольниками?
Чему равна градусная мера внутреннего угла правильного n — угольника?
Чему равна градусная мера внешнего угла правильного треугольника?
Сколько сторон имеет правильный многоугольник, если его угол равен 108 0 ?
Какой многоугольник получится, если последовательно соединить середины сторон правильного шестиугольника?

Ответы к математическому диктанту

Номер задания	Ответ
1	3, 4, 5, 7
2	5
3	3
4
5
6	5
7	6

Закрепление. Решение задач.

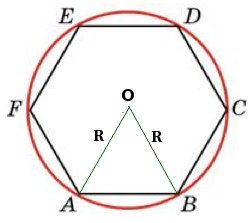
Задача №1. В правильный шестиугольник ABCDEF, со стороной 6 см, вписан правильный треугольник A₁B₁C₁. Найдите отношение радиуса окружности, вписанной в треугольник A₁B₁C₁, к радиусу окружности, вписанной в шестиугольник ABCDEF.

Найти:

ABCD — трапеция, так как — средняя линия трапеции по построению, см)

(см)

Ответ: .

Задача №2. Наглядно — поисковая задача. В правильный треугольник MNP вписана окружность. Отрезок NR перпендикулярен отрезку MP и пересекает его в точке K. Угол KMR=30 0 . Найдите радиус вписанной окружности в треугольник MNP и её длину.

правильный треугольник MNP, MR=.

Найти: OE, C (длина окружности).

MK=KP (так как центр вписанной окружности лежит на пересечении срединных перпендикуляров к сторонам треугольника). Рассмотрим треугольник MKP. MK=MR* (см). Следовательно, MP=9 см, а OE= r,

Ответ: OE =

Задача №3. Ширина кольца, образованного двумя концентрическими окружностями, равна 2. Хорда большей окружности, касательная к меньшей, равна 8. Найти радиусы окружностей.

Задача №4 . Минутная стрелка часов на здании Московского университета имеет длину 4,13 м, а часовая — 3,70м. Какой путь пройдет конец каждой из этих стрелок в течение суток?

(Ответ:14,8 м; 198,24 м.)

Задача №5 * . Основания равнобокой трапеции равны 8 см и 18 см. Найдите радиус окружности, вписанной в трапецию.

Задача №6 * . Около трапеции с высотой 6 см описана окружность. Угол между радиусами окружности, проведенными к концам боковой стороны, равен 60 0 . Найдите площадь трапеции.

Задача №7. (расчетно-практическая)

Чтобы сделать выкройку юбки «Солнце» для девочки, построим две концентрические окружности. Длина одной из этих окружностей равна длине «окружности талии» — 62см, а радиус другой больше радиуса первой на 60 см. Вычислите длину окружности по нижнему краю юбки. Сколько ткани надо иметь для пошива такой юбки? Сколько метров ленты пойдет на отделку такой юбки? (Ответ: на первый вопрос — 140 см)

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Проведите измерения и расчеты для себя.

Окружность талии = с =: см

R_талии=

С=2_юбки= :Проверь себя:

Найдите больший угол треугольника, если величины его углов образуют арифметическую прогрессию с разностью 15.

Ответ: а) 80 б) 16 в)120 г) 164 д) решения нет.

Вписанный в окружность угол, величиной 40 0 , опирается на дугу длиной 16 см. Найдите длину окружности.

Ответ: а) 164 см; б) 2 см; в) 72 см; г) 16 см; д) решения нет.

В треугольнике ABC AB=2, BC=3 и угол BAC в три раза больше угла BCA. Найдите радиус описанной окружности около этого треугольника.

Найдите центральный угол окружности радиуса 4 см, если длина соответствующей дуги равна: а) б) в) 5.

Правильные многоугольники: радиус вписанной и описанной окружности. Задание В6

Для того, чтобы научиться решать задачи из задания В6 на нахождение радиуса окружности, вписанной в правильный многоугольник, или описанной около него, не нужно запоминать большое количество формул. Нужно только вспомнить, как соотносятся стороны и углы в прямоугольном треугольнике.

И применить эти знания в немного другой ситуации.

Окружность называется описанной около многоугольника, если она проходит через все его вершины. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров, проведенных к сторонам многоугольника.

Окружность называется вписанной в многоугольник, если она касается всех сторон многоугольника. Центр вписанной окружности лежит в точке пересечения биссектрис углов многоугольника.

В правильном многоугольнике центр вписанной и описанной окружности совпадают.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Посмотрим, как соотносятся между собой радиусы вписанной и описанной окружности и сторона правильного многоугольника. Рассмотрим фрагмент правильного многоугольника:

Здесь

АВ — сторона правильного треугольника

ОК — радиус вписанной окружности

ОВ, ОА — радиусы описанной окружности

Очевидно, что треугольник АОВ — равнобедренный, поэтому ОК является высотой, биссектрисой и медианой.

Рассмотрим треугольник ОКВ. С его помощью мы найдем, как соотносятся между собой сторона правильного многоугольника, радиус вписанной и описанной окружности.

Угол AOB= , где n- количество сторон многоугольника. Тогда угол — то есть его величину мы знаем всегда.

радиус вписанной окружности r — является прилежащим катетом прямоугольного треугольника ОКВ

половина стороны многоугольника а/2 является противолежащим катетом прямоугольного треугольника ОКВ

радиус описанной окружности R является гипотенузой прямоугольного треугольника ОКВ

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Решим несколько задач из Открытого банка заданий для подготовки к ЕГЭ по математике:

1 . Задание B7 (№ 27944)

Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.

Проведем радиусы вписанной и описанной окружности и рассмотрим наш «волшебный» прямоугольный треугольник:

По условию , надо найти

Тогда

Ответ: 4

2 . Задание B7 (№ 27929)

Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.

В этой задаче мы пойдем немного другим путем, и рассмотрим треугольник АОВ:

Угол АОВ=

Найдем сторону шестиугольника. Так как все стороны правильного шестиугольника равны, . Отсюда

Треугольник АОВ равнобедренный с углом , а, значит, равносторонний. Следовательно, и

Ответ: 24.

Запомните : в правильном шестиугольнике сторона равна радиусу описанной окружности.

3 . Задание B7 (№ 27917)

Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .

Рассмотрим треугольник ВОК:

Видео:9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

Ответ: 1,5

4. Задание B7 (№ 27909)

Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.

Рассмотрим треугольник ВОК:

Ответ: 0,5

Купить видеокурс «ВСЯ ГЕОМЕТРИЯ. Часть В»

💥 Видео

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Геометрия 9 класс (Урок№22 - Формулы площади правильного многоугольника,стороны и радиуса впис.окр.)Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вписанная и описанная окружность - от bezbotvyСкачать

Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Геометрия 9 класс (Урок№26 - Построение правильных многоугольников.)Скачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Правильные многоугольники. Урок 11. Геометрия 9 классСкачать

112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

111. Окружность, вписанная в правильный многоугольникСкачать

✓ Экстремальная задача про правильный вписанный многоугольник | Ботай со мной #078 | Борис ТрушинСкачать