- Презентация к уроку
- Задачи по теме Свойства хорд, касательных и секущих к окружности. Геометрия, 8 класс.
- «Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
- Отрезки и прямые, связанные с окружностью. Теорема о бабочке
- Отрезки и прямые, связанные с окружностью
- Свойства хорд и дуг окружности
- Теоремы о длинах хорд, касательных и секущих
- Доказательства теорем о длинах хорд, касательных и секущих
- Теорема о бабочке
- 🎦 Видео
Презентация к уроку
Цель: повысить мотивацию к обучению; развивать вычислительные навыки, сообразительность, умение работать в команде.
Окружность — это линия, состоящая из всех точек плоскости, которые находятся на заданном расстоянии от одной точки плоскости, называемой центром окружности.
На слайде изображена окружность, отмечен ее центр — точка О, проведены два отрезка: ОА и СВ. Отрезок ОА соединяет центр окружности с точкой на окружности. Он называется РАДИУСОМ (по-латыни radius — “спица в колесе”). Отрезок СВ соединяет две точки окружности и проходит через ее центр. Это диаметр окружности (в переводе с греческого – “поперечник”).
Также нам понадобится определение хорды окружности — это отрезок, соединяющий две точки окружности (на рисунке – хорда DE).
Давайте выясним вопрос о взаимном расположении прямой и окружности.
Следующий вопрос и он будет основным: выяснить свойства, которыми обладают пересекающиеся хорды, секущие и касательные.
Доказывать эти свойства вы будете на уроках математики, а наша задача научиться применять эти свойства при решении задач, так как они находят широкое применение на экзаменах и в форме ЕГЭ, и в форме ГИА.
Задание для команд.
Далее продолжим работать в парах над решением простейших задач по применению этих свойств:
Используя данные на рисунке, найдите х. Слайд 5–6
Кто быстрее, правильней. С последующим обсуждением и проверкой решения всех задач. Отвечающие зарабатывают для своей команды поощрительные баллы.
Ну, а теперь приступим к решению более серьезных задач. Вашему вниманию предлагается три блока: пересекающиеся хорды, касательная и секущая, две секущие. Подробным образом разберем решение по одной задачи из каждого блока.
(Разбирается решение с подробной записью №4, №7, №12)
2. Практикум по решению задач
а) Пересекающиеся хорды
1. E – точка пересечения хорд AB и CD. AE=4, AB=10, СE:ED=1:6. Найти CD.
Решение:
2. E – точка пересечения хорд AB и CD. AB=17, CD=18, ED=2CE. Найти AE и BE.
Решение:
3. E – точка пересечения хорд AB и CD. AB=10, CD=11, BE=CE+1. Найти CE.
Решение:
4. E – точка пересечения хорд AB и CD. ED=2AE, CE=DE-1, BE=10. Найти CD.
Решение:
б) Касательная и секущая
5. Из одной точки проведены к окружности касательная и секущая. Касательная равна 6, секущая – 18. Определить внутренний отрезок секущей.
Решение:
6. Из одной точки проведены к окружности касательная и секущая. Найти касательную, если известно, что она меньше внутреннего отрезка секущей на 4 и больше внешнего отрезка на 4.
Решение:
7. Из одной точки проведены к окружности касательная и секущая. Найти секущую, если известно, что внутренний её отрезок относится к внешнему, как 3:1, а длина касательной равна 12.
Решение:
8. Из одной точки проведены к окружности касательная и секущая. Найти внешний отрезок, секущей, если известно, что внутренний её отрезок 12, а длина касательной 8.
Решение:
9. Касательная и секущая, исходящие из одной точки, соответственно равны 12 и 24. Определить радиус окружности, если секущая удалена от центра на 12.
Решение:
10. Из одной точки проведены к окружности две секущие, внутренние отрезки которых соответственно равны 8 и 16. Внешний отрезок второй секущей на 1 меньше внешнего отрезка первой. Найти длину каждой секущей.
Решение:
11. Из одной точки проведены к окружности две секущие. Внешний отрезок первой секущей относится к своему внутреннему, как 1:3. Внешний отрезок второй секущей на 1 меньше внешнего отрезка первой и относится к своему внутреннему отрезку, как 1:8. Найти длину каждой секущей.
Решение:
12. Через точку А, которая находится вне окружности на расстоянии 7 от её центра, проведен прямая, пересекающая окружность в точках В и С. Найдите длину радиуса окружности, если АВ=3, ВС=5.
Решение:
13. Из точки А проведены к окружности секущая длиной 12 см и касательная, составляющая 
Решение:
3. Закрепление знаний
Считаю, что вы обладаете достаточным запасом знаний, чтобы отправится в небольшое путешествие по лабиринтам вашего интеллекта, посетив следующие станции:
- Соображай-ка!
- Решай-ка!
- Отвечай-ка!
На станции можно находиться не более 6 минут. За каждое верное решение задачи команда получает поощрительные баллы.
Командам вручаются маршрутные листы:
| Станция | Номера задач | Отметка о решении |
| Решай-ка! | №1, №3 | |
| Соображай-ка! | №5, №8 | |
| Отвечай-ка! | №10, №11 |
| Станция | Номера задач | Отметка о решении |
| Соображай-ка! | №5, №8 | |
| Отвечай-ка! | №10, №11 | |
| Решай-ка! | №1, №3 |
| Станция | Номера задач | Отметка о решении |
| Соображай-ка! | №5, №8 | |
| Отвечай-ка! | №10, №11 | |
| Решай-ка! | №1, №3 |
4. Подведение итогов
Хотелось бы подвести итоги нашего занятия:
Помимо новых знаний надеюсь, вы лучше познакомились друг с другом, приобрели опыт работы в команде. А как вы думаете, полученные знания находят где-то применение в жизни?
Поэт Г. Лонгфелло был еще и математиком. Наверное, поэтому яркие образы, украшающие математические понятия, которые он использовал в своем романе “Каванг”, позволяют запечатлеть на всю жизнь некоторые теоремы и их применение. Читаем в романе следующую задачу:
“Лилия, на одну пядь поднимавшаяся над поверхностью воды, под порывом свежего ветра коснулась поверхности озера в двух локтях от прежнего места; исходя из этого требовалось определить глубину озера” (1 пядь равна 10 дюймам, 2 локтя – 21 дюйму).
А решается эта задача на основе свойства пересекающихся хорд. Посмотрите на рисунок, и станет ясно, как находится глубина озера.
Видео:Теорема о произведении отрезков пересекающихся хорд.Скачать

Задачи по теме Свойства хорд, касательных и секущих к окружности. Геометрия, 8 класс.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Пересекающиеся хорды окружности. Решишь задачу?Скачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
Задачи по геометрии 8 класс. Касательные, отрезки пересекающихся хорд и отрезки секущих к окружности.
Свойство пересекающихся хорд: произведение
отрезков одной хорды равно произведению
отрезков другой хорды
Хорды окружности АВ и СР пересекаются в точке Е. Найти длину отрезка РЕ, если СЕ= 8см, АЕ = 3 см, ВЕ = 6 см.
Хорды окружности АК и МЕ пересекаются в точке О. Найти длину отрезка МО, если АО= 4см, ОЕ = 5 см, ОК = 15 см.
Хорды окружности АК и МЕ пересекаются в точке О. Найти длину отрезка МО и ОЕ, если АО = 2 см, ОК = 12 см, МЕ = 10 см.
Хорды окружности АВ и СР пересекаются в точке Е. Найти длину отрезка РЕ и СЕ, если СР = 12 см, АЕ=7 см, ЕВ = 4 см.
Хорды окружности АВ и СД пересекаются в точке О. Найти длину отрезка ДО и ОС, если АО = 12 см, ОВ=4 см, ДО : ОС = 3 : 4.
Хорды окружности МК и СД пересекаются в точке А. Найти длину отрезка ДО и ОС, если МА = 6 см, АК=15 см, СА : АД = 2 : 5.
Свойство секущих к окружности, исходящих из
Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АС и ВС, если АМ = 3, МК = 5, АВ = 4.
Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АМ и МК, если АВ = 4, ВС = 6, АК = 12.
Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АВ и АС, если АМ = 2, АК = 6, длина отрезка АС на 4 больше длины отрезка АВ.
Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АМ и АК, если АВ = 2, АС = 8, длина отрезка АМ на 6 меньше длины отрезка АК.
Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АВ и ВС, если АМ = 4, АК = 6, АВ : ВС = 2 :4.
Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АМ и АК, если АМ : АК = 3 : 5, АВ = 5, ВС = 7.
Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АВ и АС, если АМ = 2, АК = 4, длина отрезка ВС на 6 больше длины отрезка АВ.
Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АМ и МК, если АМ на 8 меньше длины отрезка МК и длина отрезка АВ = 3, АС = 8.
Свойство секущей и касательной к окружности,
исходящих из одной точки:
Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АВ, если АК = 4, АР = 9.
Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АВ, если АК = 4, АР = 16.
Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АР, если АК = 4, АВ = 8.
Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АР, если АК = 5, АВ = 10.
Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АК и АР, если АВ = 5, а отрезок КР на 5 больше отрезка АК.
Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АК и АР, если АВ = 6, а отрезок КР на 6 больше отрезка АК.
Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АР и АК, если АК : КР = 4 : 5, АВ = 12.
Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АР и АК, если АК : КР = 1 : 3, АВ = 14.
Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Отрезки и прямые, связанные с окружностью. Теорема о бабочке
 Отрезки и прямые, связанные с окружностью Отрезки и прямые, связанные с окружностью |
 Свойства хорд и дуг окружности Свойства хорд и дуг окружности |
 Теоремы о длинах хорд, касательных и секущих Теоремы о длинах хорд, касательных и секущих |
 Доказательства теорем о длинах хорд, касательных и секущих Доказательства теорем о длинах хорд, касательных и секущих |
 Теорема о бабочке Теорема о бабочке |
Видео:№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства | ||||||||||||||||||||||||||
| Окружность |  | |||||||||||||||||||||||||||
| Круг |  | |||||||||||||||||||||||||||
| Радиус |  | |||||||||||||||||||||||||||
| Хорда |  | |||||||||||||||||||||||||||
| Диаметр |  | |||||||||||||||||||||||||||
| Касательная |  | |||||||||||||||||||||||||||
| Секущая |  | |||||||||||||||||||||||||||
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках
Видео:Теорема об отрезках хорд и секущихСкачать

Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде |  | Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды |  | Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины |  | Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |  | У равных дуг равны и хорды. |
| Параллельные хорды |  | Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
 |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Большая из двух хорд расположена ближе к центру окружности.

У равных дуг равны и хорды.

Дуги, заключённые между параллельными хордами, равны.
Видео:Это Свойство Поможет Решить Задачи по Геометрии — Хорда, Окружность, Секущая (Геометрия)Скачать

Теоремы о длинах хорд, касательных и секущих
| Фигура | Рисунок | Теорема | ||||||||||||||||
| Пересекающиеся хорды |  | |||||||||||||||||
| Касательные, проведённые к окружности из одной точки |  | |||||||||||||||||
| Касательная и секущая, проведённые к окружности из одной точки |  | |||||||||||||||||
| Секущие, проведённые из одной точки вне круга |  | |||||||||||||||||
| Пересекающиеся хорды | ||
 | ||
| Касательные, проведённые к окружности из одной точки | ||
 | ||
| Касательная и секущая, проведённые к окружности из одной точки | ||
 | ||
| Секущие, проведённые из одной точки вне круга | ||
 | ||
| Пересекающиеся хорды |
 |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Видео:Математика ОГЭ Задание 24 Отрезки пересекающихся хордСкачать
Доказательства теорем о длинах хорд, касательных и секущих
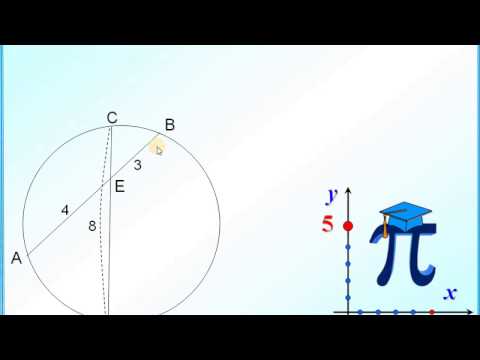
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Тогда справедливо равенство
Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Теорема о бабочке
Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
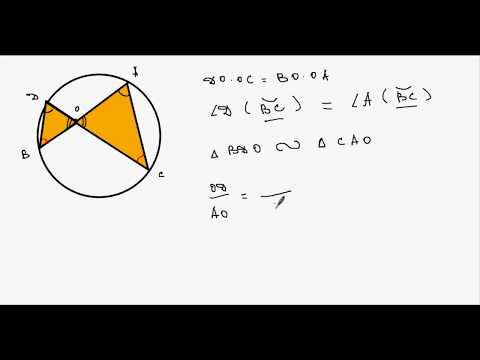
Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим
Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство
откуда вытекает равенство
что и завершает доказательство теоремы о бабочке.
🎦 Видео
ОГЭ 23 КАК РЕШИТЬ ЗАДАЧУ НА ХОРДЫ В ОКРУЖНОСТИСкачать

Окружность, диаметр, хорда геометрия 7 классСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Свойство хорд, пересекающихся внутри окружностиСкачать
Свойство пересекающихся хорд окружности. Геометрия 8-9 классСкачать

№662. Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°, ∪BC= 70°.Скачать

Геометрия В окружности проведены хорды AB и CD, пересекающиеся в точке M. Дано: AM/МВ =5/7Скачать

Свойства хорд, касательных, секущих окружности I Для решения задач из ОГЭ И ЕГЭ I Часть 1Скачать

ЕГЭ. Задачи на окружность. ХордаСкачать

Докажите, что произведение отрезков одной хорды равно произведению отрезков другой хордыСкачать

9 класс. Геометрия. Теорема о пропорциональности отрезков хорд и в секущих окружности. 22.05.2020.Скачать

Теорема о секущей и касательной, о секущих, о пересекающихся хордах | Теоремы об окружностях - 1Скачать






































