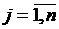Исследовать вектор 
на оптимальность в задаче ЛП:
Вначале нужно проверить, является ли вектор 
допустимым. Для этого подставляем координаты вектора в ограничения:
Так как второе ограничение выполняется как строгое неравенство, то в силу УДН для оптимальности вектора 
необходимо выполнение равенства 
.
Построим двойственную задачу:
Поскольку , то из третьего и четвертого ограничений получаем 
. Но по УДН из условия 
следует, что должно выполняться равенство в первом ограничении двойственной задачи:
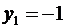
Подставляя значения 
, получим 
Следовательно, УДН не выполняются и вектор 
не является оптимальным в исходной задаче.
Метод Гомори
Постановка задачи ЦЛП
Задача целочисленного программирования (ЦЛП) формулируется так же, как и задача ЛП, но включается дополнительное требование, состоящее в том, что значения переменных, составляющих оптимальное решение, должны быть целыми неотрицательными числами:
(22)
Симплекс-метод не гарантирует целочисленности решения задачи (22), поэтому для отыскания оптимального целочисленного решения задачи ЦЛП требуются специальные методы. Один из таких методов, приводящий к целочисленному решению за конечное число шагов, предложен американским математиком Р. Гомори [1,2]. Идея метода следующая.
С помощью симплекс-метода решается задача ЛП без условия целочисленности. Если оптимальное решение получается нецелочисленным, то вводится дополнительное ограничение, которое, уменьшая многогранник допустимых решений (отсекая некоторую его часть), не исключает из него целочисленных точек. Если оптимальное решение задачи ЛП с дополнительным ограничением целочисленное, то вычисления заканчивают; если же оптимальное решение содержит хотя бы одну дробную компоненту, добавляют новое дополнительное ограничение.
Процесс присоединения дополнительных ограничений повторяют до тех пор, пока либо не будет найдено целочисленное оптимальное решение, либо показано, что задача не имеет целочисленных решений.
Алгоритм метода Гомори
Шаг 1. Симплекс-методом находим оптимальное решение задачи (22) без учета условия целочисленности. Если задача не имеет решения, то неразрешима и исходная задача ЦЛП. В этом случае алгоритм завершает работу.
Шаг 2. Пусть оптимальная таблица имеет вид:
| b |  | … |  | |
| L |  |  | … |  |
 |  |  | … |  |
| … | … | |||
 |  |  | … |  |
Если элементы 
– целочисленные, то оптимальное решение 
является целочисленным. В этом случае вычисления заканчиваем. Иначе, переходим к следующему шагу.
Шаг 3. Среди дробных компонент таблицы выбираем элемент 
с максимальной дробной частью 
и по строке i составляем дополнительное ограничение:
Здесь 
– целая часть числа 
(наибольшее целое число, не превышающее число ).
Шаг 4. Добавляем построенное ограничение к последней симплекс-таблице и, применяя двойственный симплекс-метод, находим оптимальное решение. Переходим к шагу 2.
Замечания
Признаком отсутствия целочисленного решения служит появление в таблице хотя бы одной строки с дробным свободным членом и целыми остальными коэффициентами (поскольку соответствующее уравнение неразрешимо в целых числах).
На шаге 4 двойственный симплекс-метод применяется до тех пор, пока не будет получена оптимальная симплексная таблица (возможно, потребуется несколько итераций).
Если на шаге 4 в базис вводится переменная дополнительного ограничения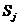 
, то эта строка вычеркивается из симплексной таблицы (соответствующее ограничение является избыточным).
Пример решения задачи ЦЛП
Решить задачу ЦЛП:
Решаем задачу без условия целочисленности симплекс-методом. Оптимальная таблица имеет вид
| b |  |  | |
| L | -14/3 | -4/3 | -2/3 |
 | 5/3 | 1/3 | 2/3 |
 | 4/3 | 2/3 | -2/3 |
Оптимальное решение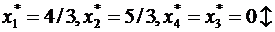 
не является целочисленным. Выберем среди нецелочисленных переменных 
переменную 
с максимальной дробной частью и построим соответствующее отсечение:
Приписывая это ограничение к симплексной таблице, и проводя стандартное преобразование двойственным симплекс-методом, получим:
| b | | | |
| L | -14/3 | -4/3 | -2/3 |
| | 5/3 | 1/3 | 2/3 |
| | 4/3 | 2/3 | -2/3 |
 | -2/3 | -1/3 | -2/3 |
| b | | | |
| L | -4 | -1 | -1 |
| | 1 | 0 | 1 |
| | 2 | 1 | -1 |
| | 1 | 1/2 | -3/2 |
Полученная таблица является оптимальной. Соответствующее оптимальное решение 
является целочисленным. Значение функции на этом решении 
.
Транспортная задача ЛП
Постановка задачи
Классическая транспортная задача ЛП формулируется следующим образом. Имеется m пунктов производства (поставщиков) и n пунктов потребления (потребителей) однородного продукта. Заданы величины:
— объем производства (запас) i-го поставщика, 
;
— объем потребления (спрос) j-го потребителя, 
— стоимость перевозки (транспортные затраты) единицы продукции от i-го поставщика к j-му потребителю.
Требуется составить такой план перевозок, при котором спрос всех потребителей был бы выполнен, и при этом общая стоимость всех перевозок была бы минимальна [1,3].
Транспортная задача, в которой суммарные запасы 
и суммарные потребности 
совпадают, называется закрытой моделью; в противном случае – открытой. Открытая модель решается приведением к закрытой модели.
Математическая закрытая модель транспортной задачи имеет вид
В случае, когда суммарные запасы превышают суммарные потребности, то есть 
, вводится фиктивный n+1 потребитель, потребности которого 
.
В случае, когда суммарные потребности превышают суммарные запасы, то есть 
, вводится фиктивный m+1 поставщик, запасы которого 
.
Стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными нулю, так как груз в обоих случаях не перевозится.
Прежде чем решать транспортную задачу, необходимо проверить, к какой модели она принадлежит, и если необходимо, то привести ее к закрытой модели.
Построение опорного плана транспортной задачи
Методы решения транспортной задачи сводятся к простым операциям с транспортной таблицей, которая имеет вид:
| 1 | … | n |  | |
| 1 |  | … |  |  |
| … | … | … | … | … |
| m |  | … |  |  |
 |  | … |  | = |
Базисными клетками транспортной таблицы являются клетки с отличными от нуля положительными перевозками, остальные клетки – свободные. Базисные клетки образуют опорный план транспортной задачи, еcли выполняются два условия:
сумма перевозок в каждой строке равна запасу 
в данной строке;
сумма перевозок в каждом столбце равна соответствующему спросу 
.
Опорный план транспортной задачи содержит не более 
отличных от нуля перевозок 
.
Опорный план называется вырожденным, если число ненулевых перевозок 
меньше , опорный план – невырожденный, если число ненулевых перевозок равно
Рассмотрим способы построения опорного плана в невырожденном и вырожденном случаях [1,3].
Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать
Методы оптимизации (стр. 2 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 |
Проверить вектор 
на оптимальность в следующей задаче ЛП:
еaijyi + cj, = 0, если хj >0 для jОJ2,
i
I – условие г)
Запишем условие г) признака оптимальности:
( т. к. 
, следовательно, в первом и третьем ограничении условия 20 двойственной задачи достигается равенство)
Пример применения признака оптимальности в развернутой форме
Проверить вектор на оптимальность в следующей задаче ЛП:
д) отсутствует, т. к. ни одно ограничение 20 основной задачи не выполняется как строгое неравенство.
Из условия г) находим 
.
Найден вектор 
. Проверяем его допустимость в двойственной задаче, т. е. выясняем, выполняются ли условия I0 и 20 двойственной задачи. Т. к. все условия выполняются, вектор y является оптимальным в двойственной задаче, а вектор х=(1, 0, 1, 0) — оптимальным в основной задаче.
Основная теорема теории линейного программирования
Для разрешимости задачи математического программирования (как и в любой оптимизационной задачи) необходимо, чтобы множество допустимых решений было не пусто, и целевая функция на этом множестве была ограничена сверху (если задача на максимум), либо снизу (если задача на минимум).
Теорема двойственности. Каковы бы ни были исходные данные, для задач 1 и 1* имеет место один из следующих взаимоисключающих случаев.
1. В задачах 1 и 1* имеются оптимальные векторы х и у и 
, т. е. обе задачи разрешимы.
2. В задаче 1 существуют допустимые векторы х из некоторого множества Х, но линейная функция 
на множестве этих векторов не ограничена сверху, т. е.
, тогда в задаче 1* нет допустимых векторов.
3. В задаче 1* существуют допустимые векторы 
, но функция 
не ограничена снизу на множестве этих векторов, т. е. 
, тогда в задаче 1 нет допустимых векторов.
4. В задачах 1 и 1* нет допустимых векторов, то есть 
Критерий разрешимости задачи ЛП
Для того, чтобы в двойственных задачах 1 и 1* существовали оптимальные векторы х и у, т. е. имел место случай 1 теоремы двойственности, достаточно выполнения одного из следующих условий:
1. в задаче 1 существует оптимальный вектор х
2. в задаче 1* существует оптимальный вектор у
3. в задаче 1 существует допустимый вектор х и функция 
ограничена сверху
4. в задаче 1* существует допустимый вектор у и функция 
ограничена снизу
5. в задачах 1 и 1* существуют допустимые векторы х и у
Следствие 2 (Необходимый признак оптимальности)
Допустимый признак оптимальности в краткой и развернутых формах является так же необходимым признаком.
Доказательство: пусть имеется оптимальный вектор х в задаче 1 и оптимальный вектор у в задаче 1*. Тогда на основании условий 2 теоремы о существовании имеет место случай 1 теоремы двойственности, то есть 
.
Экономическая интерпретация двойственных задач
Пример. С внедрением новой технологии на некотором предприятии появилась возможность использовать отходы 1,2,3 — го видов производства, получаемых в количестве 70, 30, 15 единиц в сутки соответственно для производства двух видов изделий, пользующихся большим спросом. Известно, что для производства одного изделия первого вида требуется 4, 3, 0 единиц отходов 1, 2, 3-го видов соответственно; для производства одного изделия второго вида требуется 3, 4, 3 единиц отходов 1, 2, 3-го видов. Ожидаемая прибыль от реализации продукции I и II-го видов 12 и 15 рублей соответственно. Требуется составить план производства x=
продукции I и II-го видов, обеспечивающий наибольшую прибыль (задача ЛП).
Задача I. Найти 
:
Экономическая интерпретация двойственных задач
Задача I. Найти 
:
Это же предприятие получило возможность продавать отходы производства, для чего ему необходимо определить их цену. Пусть 
— цена единицы отходов 1,2,3 — го видов. Естественно, что покупатель стремится к тому, чтобы суммарная цена всех отходов была наименьшей, а предприятию выгодно продавать их лишь в том случае, если выручка от продажи не меньше, чем прибыль от реализации готовых изделий.
Математическая модель задачи I
Задача II. Найти 
:
Задачи I и II являются парой двойственных задач.
Прямые задачи линейного программирования в канонической форме
1 каноническая форма ЛП
2 каноническая форма ЛП
Задача 1. Максимизировать линейную функцию
на множестве векторов х=( х1,х2, …хn,),
2. 
Задача 2. Максимизировать функцию
на множестве векторов 
удовлетворяющих условиям
1. 
2.
Задача 3. Максимизировать функцию
на множестве векторов 
удовлетворяющих условиям:
1.
2.
Двойственные задачи линейного программирования в канонической форме
1 каноническая форма ЛП
2 каноническая форма ЛП
Задача 1*. Минимизировать линейную функцию
на множестве векторов y=(y1,y2,…..ym),
2. 
Задача 2*. Минимизировать линейную функцию
на множестве векторов 
, удовлетворяет условиям 1.
2.
Задача 3*. Минимизировать линейную функцию
на множестве векторов , удовлетворяет условиям
2. 
Признак оптимальности для задач ЛП в канонической форме
Для оптимальности допустимого вектора х=(х1,х2…,хn,) достаточно существование m-мерного вектора у=(у1,у2,…,уm), удовлетворяющего условиям:
1 каноническая форма ЛП
2 каноническая форма ЛП
Замечание. Наиболее удобной для решения задач ЛП является 2 каноническая форма
Вторая каноническая форма задачи ЛП в векторной форме
Введем в рассмотрение m-мерные векторы: 
Тогда задачи 3 и 3* запишутся в следующей форме:
Задача А. Максимизировать линейную функцию
на множестве n-мерных векторов
1 .
, ,
Задача А*. Минимизировать линейную функцию
на множестве m-мерных векторов
удовлетворяющих системе линейных неравенств
2. 
, .
Пусть 
– m-мерное подмножество множества J.
Множество К называют базисным множеством, если отвечающие ему векторы 
являются линейно независимыми, т. е. образуют базис в пространстве Rm. Число векторов в базисном множестве К равно числу m уравнений в условии 2 задачи А:
→max
на множестве n-мерных векторов
1 ., ,
Пример. Векторы 
— линейно независимые, т. к. 
, К=<1,2>.
Допустимое базисное множество
Для каждого базисного множества 
система линейных уравнений
относительно переменных xk, 
, имеет единственное решение, отвечающее единственному разложению вектора — по соответствующим базисным векторам. Это решение можно дополнить до вектора х = (х1, х2, . . ., хn), удовлетворяющего условию 
, положив 
, 
.
Получаемый таким образом вектор х = (х1, х2, . . ., хn) будет обозначаться через х (К).
(17)
имеет единственное решение.
Если компоненты 
, то вектор 
является допустимым вектором в задаче А.
В этом случае К называют допустимым базисным множеством (ДБМ),
=( х1, х2, . . ., хm, 0,…,0).
Двойственно допустимое базисное множество
Задача А*. Минимизировать линейную функцию
на множестве m-мерных векторов
удовлетворяющих системе линейных неравенств
2. 
, .
Для любого базисного множества К единственное решение у(К) имеет система:
, 
Если вектор у(К) является допустимым в двойственной задаче А* ( т. е. удовлетворяет условию 2), то множество К называется двойственно допустимым базисным множеством (ДДБМ).
Обозначим через 
, 
.
Если 
, 
, то у(К) удовлетворяет условию 2), то есть является допустимым вектором в двойственной задаче А*.
Двойственно допустимое базисное множество
Итак, базисное множество является двойственно допустимым, если величины
, 
, (18)
, 
(19)
Отметим, что величины (18) тесно связаны с коэффициентами разложения соответствующих векторов 
по рассматриваемым базисным векторам, а именно:
, 
, (20)
где 
— коэффициенты разложения векторов 
по рассматриваемому базису, т. е. 
. (21)
Действительно, учитывая (18), (21) , , и свойства скалярного произведения, получаем
. (22)
Каково бы ни было базисное множество K, для соответствующих векторов х(К) и у (К) имеет место равенство
.
Доказательство. Так как 
, 
, 
, , получаем
,
что и требовалось показать.▄
Следствие из леммы 2 и признака оптимальности
Задача А. Максимизировать линейную функцию
на множестве n-мерных векторов
1 ., ,
Задача А*. Минимизировать линейную функцию
на множестве m-мерных векторов
удовлетворяющих системе линейных неравенств
2. 
, .
Теорема. Если базисное множество К является одновременно допустимым и двойственно допустимым базисным множеством, то отвечающие ему векторы 
и 
оптимальные соответственно в задачах А и А*.
Доказательство. Пусть К – допустимое базисное множество и двойственно допустимое базисное множество. Это значит, что вектора 
и 
— допустимые. На основании леммы 2 
, а это достаточно для того, чтобы вектор 
был оптимальным и вместе с ним и вектор 
(см. краткую форму достаточного признака оптимальности)▄
Пусть задано некоторое базисное множество К и отвечающий ему вектор
х (К) =(х1, х2, . . ., хп). Кроме того, для некоторого 
известны коэффициенты gk в разложении вектора 
по соответствующим базисным векторам:
=
.
Тогда при любом 
вектор 
=(
) с компонентами
, 
, 
, 
, 
,
удовлетворяет условию , причем значение линейной функции на этом векторе может быть вычислено по формуле
,где величина 
определяется из системы 
, 
.
Доказательство. Имеем: = (23)
После умножения соотношения (18) на и переноса всех его членов в левую часть получаем равенство: 
(24)
Складывая (19) и (20), получаем
. (26)
Следовательно, интересующий нас вектор 
удовлетворяет требуемому условию . Далее, для вектора 
выполнены равенства (в силу того, что 
, 
, , 
, и (22))
(27) ▄
Следствие 1 из леммы 3
Вектор должен удовлетворять условию неотрицательности, т. е.
.
Возможны два случая:
а). Все коэффициенты gk≤0 в
б) среди коэффициентов gk имеются положительные
Следствие 1. Если имеет место случай а), то векторы 
, определяемые в лемме 3, являются допустимыми в задаче А при всех 
, а линейная функция на множестве таких векторов не ограничена сверху.
По теореме двойственности (слайд 42) в двойственной задаче допустимый вектор не существует, следовательно, вектор х не оптимальный ▄
Следствие 2 из леммы 3
Вектор должен удовлетворять условию неотрицательности, т. е..
Случай б) среди коэффициентов gk имеются положительные
Следствие 2. Если имеет место случай б), то векторы 
являются допустимыми в задаче А лишь при 
, где
,
Пусть ; выполняется всегда; . Тогда 
, чтобы эти неравенства выполнялись одновременно, находят 
Метод последовательного улучшения допустимого вектора (МПУ)
МПУ состоит в последовательном выполнении идентичных шагов (опишем вычислительные процедуры одного шага). К началу очередного шага пусть имеются некоторое ДБМ К и отвечающий ему допустимый вектор х(K) = (х1, х2, . . ., хп). Над этими исходными данными выполняются следующие процедуры:
Зная базисные векторы 
и допустимый базисный вектор =( х1, х2, . . ., хm, 0,…,0), решаем систему линейных уравнений:
Эта система имеет единственное решение 
, т. к. К – это базисное множество.
Метод последовательного улучшения допустимого вектора (МПУ)
II. Проверка двойственной допустимости ДБМ К. Для найденного вектора у(К) вычисляются величины 
и проверяются неравенства , 
.
1. Находим величины 
При этом возможны два случая:
а) 
. Это означает, что базисное множество К является одновременно допустимым и двойственно допустимым базисным множеством. Тогда (по теореме: если базисное множество К является одновременно допустимым и двойственно допустимым базисным множеством, то отвечающие ему векторы и оптимальные соответственно в задачах А и А*) векторы х(К) и у (К) оптимальны для соответствующих задач и . На этом процесс заканчивается с выдачей искомых оптимальных векторов.
б) условие а) нарушается, т. е. К не является двойственно допустимым и вектор 
не допустимый в задаче А*. Надо найти 
и перейти к выполнению следующей процедуры.
Метод последовательного улучшения допустимого вектора (МПУ)
III. Вычисление коэффициентов разложения вектора 
по базисным векторам.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать
Примеры решений по векторной алгебре
Видео:Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать
Векторная алгебра для чайников
В этом разделе вы найдете бесплатные решения задач по векторной алгебре: вектора, углы, взаимное расположение на плоскости и пространстве, базис из векторов, действия с векторами и т.п.
Видео:ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать
Решения задач с векторами
Задача 1. На оси $Ох$ найти точку, равноудаленную от точек $А(2;-4;5)$ и $В(-3;2;7)$.
Задача 2. Написать разложение вектора $X$ по векторам $(a, b, c)$.
Задача 3. Найти косинус угла между векторами $AB$ и $AC$.
Задача 4. Вычислить площадь треугольника с вершинами $$A=(-4;4;4), B=(3;1;0), C=(-1;0;6).$$
Задача 5. Компланарны ли вектора $a, b, c$? $$a=(-3;2;1), b=(3;1;2), c=(3;-1;4)$$
Задача 6. Заданы два вектора в пространстве. Найти:
а) их сумму;
б) их разность; косинус угла между ними;
в) их векторное произведение.
$a=(0;1;1), b=(-2;0;1).$
Задача 7. Сила $F$ приложена к точке $А$. Вычислить:
а) работу силы $F$ в случае, когда точка её приложения, двигаясь прямолинейно, перемещается в точку $В$;
b) модуль момента силы $F$ относительно точки $В$.
Задача 8. Найти ранг и базис системы векторов, перейти к новому базису. Записать разложения векторов по найденным базисам.
Задача 11. Написать разложение вектора $bar$ по векторам $bar, bar, bar$.
Задача 13. Вычислить площадь параллелограмма, построенного на векторах $bar
$, $bar$.
📽️ Видео
ВЕКТОРЫ решение задач 9 класс АтанасянСкачать
ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать
Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать
8 класс, 48 урок, Применение векторов к решению задачСкачать
18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать
Вычитание векторов. 9 класс.Скачать
Урок 11. Решение задач на действия с векторамиСкачать
Геометрия 10 класс (Урок№18 - Компланарные векторы. Векторный метод решения задач.)Скачать
ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать
Координаты вектора. 9 класс.Скачать
Формулы векторов через координаты. Практическая часть. 9 класс.Скачать
Векторное произведение векторов решение задачСкачать
КООРДИНАТЫ ВЕКТОРА В ПРОСТРАНСТВЕ решение задачСкачать
Скалярное произведение векторов. 9 класс.Скачать
Математика без Ху!ни. Смешанное произведение векторовСкачать
Умножение вектора на число. 9 класс.Скачать
