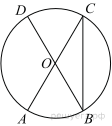Задачи на окружность 7

В разработке представлена подборка задач для 7 класса по геометрии по теме «Окружность». Задания взяты из открытого банка заданий ОГЭ демоверсии 2020 (№17 и№25)

Просмотр содержимого документа
«Задачи по геометрии для 7 класса по теме «Окружность» по материалам открытого банка заданий ОГЭ №17 и №25 демоверсии 2020»

Задачи по теме « Окружность» 7 класс

Цен­траль­ный угол AOB опи­ра­ет­ся на хорду AB дли­ной 6. При этом угол OAB равен 60°. Най­ди­те радиус окружности.

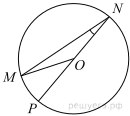
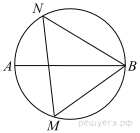
Найдите гра­дус­ную меру ∠MON, если известно, NP — диаметр, а гра­дус­ная мера ∠MNP равна 18°.

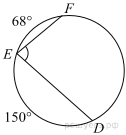
Найдите ∠DEF, если гра­дус­ные меры дуг DE и EF равны 150° и 68° соответственно.

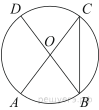
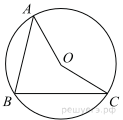
В окруж­но­сти с цен­тром O AC и BD — диаметры. Угол ACB равен 26°. Най­ди­те угол AOD. Ответ дайте в градусах.

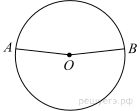
Точки A и B делят окруж­ность на две дуги, длины ко­то­рых относятся как 9:11. Най­ди­те величину цен­траль­но­го угла, опи­ра­ю­ще­го­ся на мень­шую из дуг. Ответ дайте в градусах.

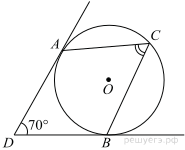
В угол ве­ли­чи­ной 70° впи­са­на окружность, ко­то­рая ка­са­ет­ся его сто­рон в точ­ках A и B. На одной из дуг этой окруж­но­сти вы­бра­ли точку C так, как по­ка­за­но на рисунке. Най­ди­те ве­ли­чи­ну угла ACB.

Величина цен­траль­но­го угла AOD равна 110°. Най­ди­те величину впи­сан­но­го угла ACB. Ответ дайте в градусах.

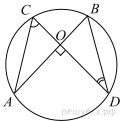
Точки A, B, C и D лежат на одной окруж­но­сти так, что хорды AB и СD вза­им­но перпендикулярны, а ∠BDC = 25°. Най­ди­те величину угла ACD.

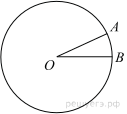
На окруж­но­сти с цен­тром O от­ме­че­ны точки A и B так, что 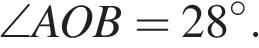Длина мень­шей дуги AB равна 63. Най­ди­те длину боль­шей дуги.

На окруж­но­сти по раз­ные стороны от диа­мет­ра AB взяты точки M и N. Известно, что ∠NBA = 38°. Най­ди­те угол NMB. Ответ дайте в градусах.

Точка O – центр окружности, на ко­то­рой лежат точки A, B и C. Известно, что ∠ABC = 15° и ∠OAB = 8°. Най­ди­те угол BCO. Ответ дайте в градусах.

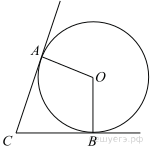
В угол C ве­ли­чи­ной 83° впи­са­на окружность, ко­то­рая ка­са­ет­ся сто­рон угла в точ­ках A и B. Най­ди­те угол AOB. Ответ дайте в градусах.

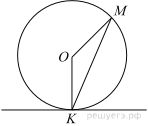
Прямая ка­са­ет­ся окруж­но­сти в точке K. Точка O — центр окружности. Хорда KM об­ра­зу­ет с ка­са­тель­ной угол, рав­ный 83°. Най­ди­те ве­ли­чи­ну угла OMK. Ответ дайте в градусах.

Касательные в точ­ках A и B к окруж­но­сти с цен­тром O пе­ре­се­ка­ют­ся под углом 72°. Най­ди­те угол ABO. Ответ дайте в градусах.

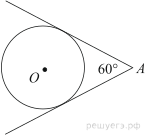
Из точки А про­ве­де­ны две ка­са­тель­ные к окруж­но­сти с цен­тром в точке О. Най­ди­те ра­ди­ус окружности, если угол между ка­са­тель­ны­ми равен 60°, а рас­сто­я­ние от точки А до точки О равно 8.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Задачи на окружность. 7 класс.

Видео:Окружность. 7 класс.Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 74°. Найдите угол AOD. Ответ дайте в градусах.

В окружности с центром O отрезки AC и BD — диаметры. Угол AOD равен 132°. Найдите угол ACB. Ответ дайте в градусах.

Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ ABC=46° и ∠ OAB=27°. Найдите угол BCO. Ответ дайте в градусах.

Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ ABC=50° и ∠ OAB=35°. Найдите угол BCO. Ответ дайте в градусах.

Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 39°. Найдите величину угла OMK. Ответ дайте в градусах.

Прямая касается окружности в точке K. Центр окружности — точка O. Хорда KM образует с касательной угол, равный 40°. Найдите величину угла KOM. Ответ дайте в градусах.

Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 6.

Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.

Касательные в точках A и B к окружности с центром O пересекаются под углом 68°. Найдите угол ABO. Ответ дайте в градусах.

В угол C величиной 107° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.

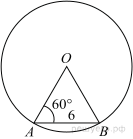
Угол AOB опирается на хорду АВ длиной 6. При этом угол ОАВ равен 60°. Найдите радиус окружности.

В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 80°. Найдите величину угла OAB.

Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 931 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 701 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 335 человек из 72 регионов

Ищем педагогов в команду «Инфоурок»

• Макарова Светлана ГригорьевнаНаписать 4827 26.05.2020

Номер материала: ДБ-1181654

25.05.2020 0

25.05.2020 0

25.05.2020 0

22.05.2020 0

19.05.2020 0

15.05.2020 0

14.05.2020 0

14.05.2020 0

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме обсудят введение обязательных тестов на наркотики в школах

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Утвержден список федеральных инновационных площадок в образовании на 2022 год

Время чтения: 1 минута

Онлайн-конференция об управлении общеобразовательной организацией

Время чтения: 2 минуты

Детский омбудсмен предложила ужесточить наказание за преступления против детей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:ОКРУЖНОСТЬ задачи на построение 7 класс АтанасянСкачать

Геометрия. 7 класс

Конспект урока

Окружность. Задачи на построение

Перечень рассматриваемых вопросов:

• Геометрическое место точек, примеры ГМТ.
• Изображение на рисунке окружности и ее элементов.
• Решение задач на построение.
• Выполнение построений прямого угла, отрезка, угла равного данному, биссектрисы угла, перпендикулярных прямых, середины отрезка с помощью циркуля и линейки.

Радиус окружности – отрезок соединяющий центр окружности с какой-либо точкой окружности.

Окружность – это геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.

Хорда – отрезок, соединяющий две точки окружности.

Диаметр – хорда, проходящая через центр окружности.

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

1. Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
2. Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
3. Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
4. Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
5. Иченская М.А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М.А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Ранее мы узнали некоторые геометрические фигуры, например, угол, отрезок, треугольник, научились их строить и измерять. Сегодня мы введём определение ещё одной фигуры – окружности, рассмотрим её элементы и выполним построения геометрических фигур с помощью циркуля и линейки.

Для начала дадим определение геометрической фигуры, называемой окружностью.

Окружность – это геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.

Но можно использовать и другое определение окружности.

Окружность ‑ это геометрическое место точек, удалённых на одно и то же расстояние от точки, называемой центром окружности. Это расстояние называют радиусом окружности. В нашем случае точки О.

При этом стоит пояснить, что геометрическое место точек – это фигура речи, употребляемая в математике для определения геометрической фигуры, как множества всех точек, обладающих некоторым свойством.

Вспомним элементы окружности.

Радиус окружности – отрезок соединяющий центр окружности с какой-либо точкой окружности.

По определению окружности все её радиусы имеют одну и ту же длину. OM = OA

Отрезок, соединяющий две точки окружности, называется хордой.

Хорда, проходящая через центр окружности, называется диаметром.

O – середина диаметра.

Любые две точки окружности делят её на две части. Каждая из этих частей называется дугой окружности.

AMB, ALB – дуги окружности.

Построим окружность радиусом 3 см. Для этого поставим точку О. Возьмём циркуль и выставим с помощью линейки расстояние между ножками циркуля, равное 3 см. Поставим иголочку циркуля в точку О и построим окружность, вращая ножку циркуля с грифелем вокруг этой точки. Грифель описывает замкнутую кривую линию, которую называют окружностью.

Часть плоскости, которая лежит внутри окружности, вместе с самой окружностью, называют кругом, т. е. окружность ‑ граница круга.

Итак, мы можем с помощью циркуля строить окружность, но с его помощью можно построить и угол равный данному. Для построения воспользуемся ещё и линейкой.

Построить: EOМ = A.

1. Окр. (A; r), r – произвольный радиус.

2. Окр. (A; r) ∩ AB = B.

3. Окр. (A; r) ∩ AС = С.

4. Окр. (O; r) ∩ OM = D.

5. Окр. (D; BС) ∩ Окр. (O; r) = E

6. OЕ, ЕОD = BAC (из равенства ∆ОЕD и ∆ABC). EOM – искомый.

Теперь выполним построение биссектрисы угла.

Построить: AE – биссектриса CAB.

1. Окр. (A; r), r – произвольный радиус.

1. Окр. (A; r) ∩ AB = B.
2. Окр. (A; r) ∩ AC = C.
3. Окр. (C; CB) ∩ Окр. (B; CB) = E.
4. AE – искомая биссектриса BAC, т. к. ABE =CBE (из равенства ∆ACE и ∆ABE).

Рассмотрим ещё одно построение с помощью циркуля и линейки. Построим середину отрезка АВ.

Для этого построим две окружности с центрами на концах отрезка , т. е. в точках А и В. Окружности пересекутся в точках Р и Q. Проведём прямую через точки Р и Q. Прямая РQ пересечёт прямую АВ в точке О, которая и будет являться искомой серединой отрезка АВ. Докажем это. Для этого рассмотрим ∆APQ и ∆BPQ. Они равны по трём сторонам, следовательно, ∠1 = ∠2, поэтому РО– биссектриса равнобедренного ∆АВР, а соответственно РО ещё и медиана. Следовательно, точка О – середина отрезка АВ.

Разбор заданий тренировочного модуля.

№ 1. АВ и СК – диаметры окружности, с центром в точке О. По какому признаку равенства треугольников равны треугольники АОС и ОКВ?

Так как О – центр окружности, то точка О делит диаметры пополам, следовательно отрезки АО, ОВ, ОС, ОК равны. ∠СОА = ∠КОВ (как вертикальные). Поэтому треугольники АОС и ОКВ равны по первому признаку равенства треугольников (по двум сторонам и углу между ними).

Ответ: 1 признак равенства треугольников.

№ 2. На рисунке O – центр окружности, АВ – диаметр окружности. Отрезки АD и ВС, перпендикулярны к отрезку АВ. АВ = 8 см, ОС = 5 см, СВ = 3 см. Чему равен периметр ∆AOD?

Периметр треугольника AOD равен сумме сторон АО, AD, DO. Найдём эти стороны.

По условию O – центр окружности, то она делит диаметр пополам, следовательно отрезок АО равен отрезку ОВ, т. е. АО = АВ:2 = 8 см :2 = 4 см.

По условию отрезки АD и ВС, перпендикулярны к отрезку АВ, следовательно ∠СВО = ∠ОАD = 90°, ∠АОD = ∠СОВ (как вертикальные). Поэтому ∆АОD = ∆СОВ (по 2 признаку равенства треугольников). Следовательно, AD = СВ = 3 см, DO = ОС = 5 см.

Р_∆AOD = АО + AD + DO = 4 см + 3 см + 5 см = 12 см.

💡 Видео

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

7 класс, 21 урок, ОкружностьСкачать

7 класс, 23 урок, Примеры задач на построениеСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

7 класс.Задачи на окружностьСкачать

Окружность и задачи на построениеСкачать

Урок 3 Окружность и круг (7 класс)Скачать

Урок 7. Окружность, круг и их элементы. ОГЭ. Вебинар |МатематикаСкачать

Вся геометрия 7–9 класс с нуля | ОГЭ МАТЕМАТИКА 2023Скачать

Геометрия. Окружность с нуля. Основы. Теоремы и задачи (примеры). 7 класс.Скачать

Свойство диаметра окружности. 7 класс.Скачать

7 класс геометрия. Окружность. Решение задач. Урок 2Скачать

Задачи на построение с помощью циркуля и линейки - 7 класс геометрияСкачать

РЕШЕНИЕ ЗАДАЧИ ПО ТЕМЕ «ОКРУЖНОСТЬ И КРУГ». Задачи | ГЕОМЕТРИЯ 7 классСкачать

7 класс - Геометрия - Задачи на построение. Окружность. Деление отрезка пополам.Скачать

КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать