Задачи на график окружности (4 видео) | Курс школьной геометрии

Графический метод решения задач с параметрами

Теперь вы узнали, что такое параметр, и увидели решение самых простых задач.

Но подождите — рано успокаиваться и говорить, что вы все знаете. Есть множество типов задач с параметрами и приемов их решения. Чтобы чувствовать себя уверенно, мало посмотреть решения трех незатейливых задач.

Вот список тем, которые стоит повторить:

1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».

Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому. Конечно, он не единственный. Но начинать лучше всего именно с него.

Мы разберем несколько самых простых задач, решаемых графическим методом. Больше задач — в видеокурсе «Графический метод решения задач с параметрами» (бесплатно).

1. При каких значениях параметра a уравнение имеет ровно 2 различных решения?

Дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель не равен нулю.

В первом уравнении выделим полный квадрат:

Это уравнение окружности с центром в точке и радиусом равным 2. Обратите внимание — графики будем строить в координатах х; а.

Уравнение задает прямую, проходящую через начало координат. Нам нужны ординаты точек, лежащих на окружности и не лежащих на этой прямой.

Для того чтобы точка лежала на окружности, ее ордината а должна быть не меньше 0 и не больше 4.

Кроме того, точка не должна лежать на прямой , которая пересекает окружность в точках и Координаты этих точек легко найти, подставим в уравнение окружности.

Точка С также не подходит нам, поскольку при мы получим единственную точку, лежащую на окружности, и единственное решение уравнения.

2. Найдите все значения a, при которых уравнение имеет единственное решение.

Уравнение равносильно системе:

Мы возвели обе части уравнения в квадрат при условии, что (смотри тему «Иррациональные уравнения»).

Раскроем скобки в правой части уравнения, применяя формулу квадрата трехчлена. Получаем систему.

Приводим подобные слагаемые в уравнении.

Заметим, что при прибавлении к правой и левой части числа 49 можно выделить полные квадраты:

Решим систему графически:

Уравнение задает окружность с центром в точке , где радиус

Неравенство задает полуплоскость, которая расположена выше прямой , вместе с самой этой прямой.

Исходное уравнение имеет единственное решение, если окружность имеет единственную общую точку с полуплоскостью. Другими словами, окружность касается прямой, заданной уравнением

Пусть С — точка касания.

На координатной плоскости отметим точки и , в которых прямая пересекает оси Y и Х.

Рассмотрим треугольник ABP. Он прямоугольный, и радиус окружности PC является медианой этого треугольника. Значит по свойству медианы прямоугольного треугольника, проведенной к гипотенузе.

Из треугольника ABP найдем длину гипотенузы AB по теореме Пифагора.

Решая это уравнение, получаем, что

3. Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение.

График уравнения — окружность с центром и радиусом равным 2.

График уравнения — две симметричные окружности и радиуса 2 c центрами в точках и

Второе уравнение при задает окружность с центром в точке и радиусом a.

Вот такая картинка, похожая на злую птицу. Или на хрюшку. Кому что нравится.

Система имеет единственное решение в случаях, когда окружность , задаваемая вторым уравнением, касается только левой окружности или только правой

Если a — радиус окружности , то это значит, что (только правая) или (только левая).

Пусть А — точка касания окружности и окружности

, (как гипотенуза прямоугольного треугольника МNР с катетами 3 и 4),

В — точка касания окружности и окружности

длину MQ найдем как гипотенузу прямоугольного треугольника KMQ с катетами 7 и 4; Тогда для точки В получим:

Есть еще точки С и D, в которых окружность касается окружности или окружности соответственно. Однако эти точки нам не подходят. В самом деле, для точки С:

, но и это значит, что окружность с центром в точке М, проходящая через точку С, будет пересекать левую окружность и система будет иметь не одно, а три решения.

Аналогично, для точки D:

и значит, окружность с центром М, проходящая через точку D, будет пересекать правую окружность и система будет иметь три решения.

4. При каких значениях a система уравнений имеет 4 решения?

Конечно же, решаем графически. Только непуганый безумец возьмется решать такую систему аналитически : -)

И в первом, и во втором уравнении системы уже можно разглядеть известные «базовые элементы» (ссылка) — в первом ромбик, во втором окружность. Видите их? Как, еще нет? — Сейчас увидите!

Просто выделили полный квадрат во втором уравнении.

Сделаем замену Система примет вид:

Вот теперь все видно! Рисовать будем в координатах

Графиком первого уравнения является ромб, проходящий через точки с координатами и

Графиком второго уравнения является окружность с радиусом и центром в начале координат.

Когда же система имеет ровно 4 решения?

1) В случае, когда окружность вписана в ромб, то есть касается всех сторон ромба.

Запишем площадь ромба двумя способами — как произведение диагоналей пополам и как произведение стороны на высоту, проведенную к этой стороне.

Диагонали нашего ромба равны 8 и 6. Значит,

Сторону ромба найдем по теореме Пифагора. Видите на рисунке прямоугольный треугольник со катетами 3 и 4? Да, это египетский треугольник, и его гипотенуза, то есть сторона ромба, равна 5. Если h — высота ромба, то

При этом Мы помним, что если окружность вписана в ромб, то диаметр этой окружности равен высоте ромба. Отсюда

Мы получили ответ:

2) Есть второй случай, и мы его найдем.

Давайте посмотрим — если уменьшить радиус окружности, сделав , окружность будет лежать внутри ромба, не касаясь его сторон. Система не будет иметь решений, и нам это не подходит.

Пусть радиус окружности больше, чем , но меньше 3. Окружность дважды пересекает каждую из четырех сторон ромба, и система имеет целых 8 решений. Опять не то.

Пусть радиус окружности равен 3. Тогда система имеет 6 решений.

А что, если ? Окружность пересекает каждую сторону ромба ровно 1 раз, всего 4 решения. Подходит!

Значит, Объединим случаи и запишем ответ:

Больше задач и методов решения — на онлайн-курсе Анны Малковой. И на интенсивах ЕГЭ-Студии в Москве.

Содержание

Решение задач по теме «УРАВНЕНИЕ ОКРУЖНОСТИ»
Просмотр содержимого документа «Решение задач по теме «УРАВНЕНИЕ ОКРУЖНОСТИ»»
Решение задач по теме: «Уравнение окружностей»
Ход урока
I. Организационный момент.
2. Знакомство с командами (представление презентаций, Приложение 2 ).
3. Актуализация знаний учащихся.
4. Разминка.
📺 Видео

Видео:УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Решение задач по теме «УРАВНЕНИЕ ОКРУЖНОСТИ»

В презентации к уроку геометрии для 9 класса представлены задачи по теме «Уравнение окружности».

Просмотр содержимого документа
«Решение задач по теме «УРАВНЕНИЕ ОКРУЖНОСТИ»»

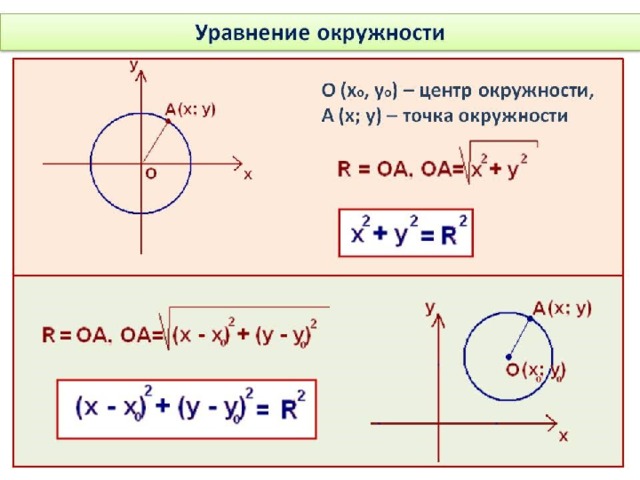
Определите по уравнению окружности координаты ее центра и радиус :

А) (Х+2)² + ( У – 5)² = 49

Б) (Х+7)² + ( У + 1)² = 36

Ответ : О (-7; -1); R= 6

В) (Х- 6)² + ( У + 15)² = 81

Ответ : О (6; -15); R= 9

Ответ : О (0; 9); R= V͞2

Составьте уравнение окружности, если известны координаты ее центра М и радиус R :

В) М ( 1; -1) , R = ; = V͞11

Задание № 2 ( проверка)

Составьте уравнение окружности с центром в точке М (1; -4), проходящей через точку А(0; 3).

Составьте уравнение окружности, диаметром которой является отрезок АВ,

если А( -4; 7), В ( 2; 5 )

Составьте уравнение окружности, радиусом которой является отрезок КР,

если К (-2; 3), Р ( 5; — 23)

Составьте уравнение окружности с центром в точке

А(-4; 2), которая касается оси ординат.

Составьте уравнение окружности, проходящей через точку А( 1; -5 ), центр которой принадлежит оси абсцисс, а радиус равен 13.

Докажите, что данное уравнение является уравнением окружности, и укажите координаты центра и радиус этой окружности:

А) Х² + У² + 6х – 14у – 5 = 0;

Найдите координаты центра и радиус окружности ,заданной уравнением

Х² + У² — 18х +2у + 50 = 0. Определите положение точек

А(5; -1), В(2; 4) и С( 13; — 5 ) относительно этой окружности.

Видео:Уравнение окружности (1)Скачать

Решение задач по теме: «Уравнение окружностей»

Разделы: Математика

За неделю до проведения урока класс делится на четыре группы. Каждая готовит презентацию, отражающую название команды.

1. Образовательные:

систематизация знаний, умений и навыков по теме “Метод координат”,

совершенствование навыков решения задач.

2. Развивающие:

развитие математически грамотной речи,

логического мышления,

культуры диалога.

3. Воспитательные:

воспитывать познавательную активность,

культуру общения,

культуру диалога.

Ход урока

I. Организационный момент.

В начале урока выдается командам оценочный лист ( Приложение 1 ) с целью самостоятельной оценки учащимися степени участия каждого члена команды в подготовке к уроку и его проведении.

Рассказываются правила урока. За каждое правильное решение команде выдается лепесток определенного цвета:

все ответы верные – красный;
одна ошибка – зеленый;
две ошибки – жёлтый.

Лепестки крепятся на магнитную доску, образуя цветок.

Итоговая оценка выставляется с учетом этого бланка, а также учитывается количество и цвет набранных командой лепестков в цветке на доске.

2. Знакомство с командами (представление презентаций, Приложение 2 ).

3. Актуализация знаний учащихся.

– На последних уроках геометрии мы познакомились с еще одним способом решения задач МЕТОДОМ КООРДИНАТ.

Задавая фигуры уравнением и выражая в координатах геометрические соотношения, мы применяем алгебру к геометрии. Так мы поступили, когда выразили через координаты основную геометрическую величину – расстояние между точками, а затем, когда вывели уравнение окружности и прямой.

Пользуясь координатами, можно истолковывать уравнения и неравенства геометрически и таким образом применять геометрию к алгебре и анализу. Графическое изображение функций – первый пример такого применения метода координат

Метод координат в соединении с алгеброй составляет раздел геометрии, называемый “Аналитической геометрией”.

Сегодня я предлагаю еще раз поговорить об уравнении окружности и проследить, как алгебра помогает в решении геометрических задач.

4. Разминка.

– На доске записан ряд уравнений. Какие фигуры они задают?

Команды получают карточки с заданием. Время обдумывания 2мин.

По истечению времени идет опрос команд по очереди.

1	7.
2.	8.
3.	9.
4.	10.
5.	11.
6.	12.

Последнее уравнение вызывает сомнения т.к. ранее не встречалось в таком виде.

Учитель показывает как, выделив полный квадрат, получить уравнение окружности.

Оценить результат работы команд.

Выясните, будет ли данные уравнения задавать окружность, если да, то укажите радиус и координаты центра. Если нет, то почему?

Каждая из команд получают свою карточку. Время 7 минут.

1.	1.
2.	2.
3.	3.

1.	1.
2	2
3	3

Последние уравнение в каждой карточке не задает окружность, и учащиеся поясняют почему. Оценить ответы.

1. Как могут взаимораспологаться две окружности? Дается время(3 мин.). Предлогается ребятам нарисовать различные варианты на ватмане и показать рисунки. После демонстрации и обсуждения всевозможных вариантов Предлогается следующая задача.

2. Как взаиморасположены линии заданные уравнениями?

Изобразите ответ на обратной стороне ватмана (на нем, заранее, нанесена система координат.)

Ответ:

Значит: первая внутри второй.

Результат этого задания оценивается следующим образом:

Команда, выполнившая первая – красный; вторая – зеленый; третья – желтый

После подведения итогов предлагается задача общая для всех команд.

Командам выдается карточка с кратким описанием условия. Текст задачи зачитывается.

Окружность задана уравнением .

Точка с координатами (5;4) является центром другой окружности касающейся первой внешним образом. Напишите уравнение этой окружности.

Вопросы для обсуждения:

-Поможет ли рисунок в решении задачи?

-Что можно узнать из уравнения первой окружности?

-Что надо знать, чтобы записать уравнение второй окружности?

-Как можно узнать радиус второй окружности?

Ответ:

Перед следующим заданием полезно повторить:

Какая окружность называется описанной около треугольника?

Что значит, точка принадлежит графику уравнения?

Что необходимо знать для написания уравнения окружности?

Написать уравнение окружности описанной около треугольника с заданными координатами вершин.

Какие, алгебраические, приемы могут быть использованы для решения поставленной задачи? (составление систем уравнений и приемы их решения).

3. С (3;-7)	4. В (1;-4)
Д (8;-2)	К (4;5)
К (6;2)	Д (3;-2)

1.	2.
3.	4.

Следующую задачу решает учитель.

Задача: Что представляет собой множество точек плоскости, отношение расстояний от которых до двух данных точек есть величина постоянная?

Решение: Впервые эту задачу сформулировал и решил Аполлоний Пергский, (260-170 гг. до н.э.)

Решение получилось очень сложное – поскольку применены геометрические приемы. Однако в работах французского математика Рене Декарта эта задача решена более элегантно. Декарт применил метод координат.

Я предлагаю посмотреть на это решение. Итак, пусть даны две точки ,А и В и некоторое положительное число k, равное отношению расстояний до точки М.

1случай. Если k=1,тогда множество точек М есть серединный перпендикуляр к отрезку АВ.

2 случай. Пусть k целое не отрицательное число не равное 1

Для удобства решения возьмем k=2 , т.е. МА: МВ=2.

Введем систему прямоугольных координат. Совместим начало отсчета с точкой В. В качестве положительной полуоси x возьмем луч ВА. (рис.2)

Тогда получим следующие координаты точек: В(0,0), А(a,0), М(x,y). Пусть a=3 опять для простоты рассуждений.

Тогда, пользуясь формулами расстояния между двумя точками, запишем: