Формула пика для окружности

Видео:Формула ПикаСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Автор: Сажина Валерия Андреевна, учащаяся 9 класса МАОУ «СОШ№11» г Усть-Илимск Иркутской области

Руководитель: Губарь Оксана Михайловна, учитель математики высшей квалификационной категории МАОУ «СОШ№11» г Усть-Илимск Иркутской области

Видео:#239. ДОКАЗАТЕЛЬСТВО, которое от вас скрывали!Скачать

Оглавление

Видео:Формула Пика или Как найти площадь любой фигуры на клетчатой бумагеСкачать

Введение

При изучении темы геометрии «Площади многоугольников», я решила узнать: существует ли способ нахождения площадей, отличный от тех, которые мы изучали на уроках?

Таким способом является формула Пика. Л. В. Горина в «Материалах для самообразования учащихся» так описывала данную формулу: «Ознакомление с формулой Пика особенно актуально накануне сдачи ЕГЭ и ГИА. С помощью этой формулы можно без проблем решать большой класс задач, предлагаемых на экзаменах, — это задачи на нахождение площади многоугольника, изображённого на клетчатой бумаге. Маленькая формула Пика заменит целый комплект формул, необходимых для решения таких задач. Формула Пика будет работать «одна за всех…»!»[2].

В материалах ЕГЭ мне встретились задачи с практическим содержанием на нахождение площади земельных участков[7]. Я решила проверить, применима ли данная формула для нахождения площади территории школы, микрорайонов города, области. А так же рационально ли ее применение для решения задач.

Объект исследования: формула Пика.

Предмет исследования: рациональность применение формулы Пика при решении задач.

Цель работы: обосновать рациональность использования формулы Пика при решении задач на нахождение площади фигур, изображённых на клетчатой бумаге.

Методы исследования: моделирование, сравнение, обобщение, аналогии, изучение литературных и Интернет-ресурсов, анализ и классификация информации.

— подобрать необходимую литературу, проанализировать и систематизировать полученную информацию;

— рассмотреть различные методы и приёмы решения задач на клетчатой бумаге;

— проверить экспериментальным путем рациональность использования формулы Пика;

— рассмотреть применение данной формулы.

Гипотеза: если применить формулу Пика для нахождения площадей многоугольника, то можно найти площадь территории, а решение задач на клетчатой бумаге будет более рационально.

Видео:Формула Пика / Как находить площадь многоугольника?Скачать

Основная часть

Видео:Кто угадает ФОРМУЛУ ПИКА - получит 1000 рублей!Скачать

Теоретическая часть

Клетчатая бумага (точнее — ее узлы), на которой мы часто предпочитаем рисовать и чертить, является одним из важнейших примеров точечной решетки на плоскости. Уже эта простая решетка послужила К. Гауссу отправной точкой для сравнения площади круга с числом точек с целыми координатами, находящихся внутри него. То, что некоторые простые геометрические утверждения о фигурах на плоскости имеют глубокие следствия в арифметических исследованиях, было в явном виде замечено Г. Минковским в 1896 г., когда он впервые для рассмотрения теоретико-числовых проблем привлек геометрические методы [4].

Нарисуем на клетчатой бумаге какой-нибудь многоугольник (Приложение 1, рисунок 1). Попробуем теперь рассчитать его площадь. Как это сделать? Наверное, проще всего разбить его на прямоугольные треугольники и трапецию, площади которых уже нетрудно вычислить и сложить полученные результаты.

Использованный способ несложен, но очень громоздок, кроме того он годится не для всяких многоугольников. Так следующий многоугольник нельзя разбить на прямоугольные треугольники, так как мы это проделали в предыдущем случае (Приложение 2, рисунок 2). Можно, например, попробовать дополнить его до «хорошего», нужного нам, то есть до такого, площадь которого мы сможем вычислить описанным способом, потом из полученного числа вычесть площади добавленных частей.

Однако оказывается, что есть очень простая формула, позволяющая вычислить площади таких многоугольников с вершинами в узлах квадратной сетки.

Эту формулу открыл австрийский математик Пик Георг Александров (1859 – 1943 г.г.) в 1899 году. Кроме этой формулы Георг Пик открыл теоремы Пика, Пика – Жюлиа, Пика – Невалины, доказал неравенство Шварца – Пика.

Эта формула оставалась незамеченной в течение некоторого времени после того, как Пик её опубликовал, однако в 1949 г. польский математик Гуго Штейнгауз включил теорему в свой знаменитый «Математический калейдоскоп». С этого времени теорема Пика стала широко известна. В Германии формула Пика включена в школьные учебники[2].

Она является классическим результатом комбинаторной геометрии и геометрии чисел.

Доказательство формулы Пика

Пусть АВС D – прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки (Приложение 3, рисунок 3).

Обозначим через В — количество узлов, лежащих внутри прямоугольника, а через Г — количество узлов на его границе. Сместим сетку на полклетки вправо и полклетки

вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещённой сетки, а каждый из Г узлов – 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника S равна

S = В + + 4 · = В + — 1 .

Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, мы установили формулу S = В + — 1 . Это и есть формула Пика.

Оказывается, эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки.

Видео:Памяти Формулы ПикаСкачать

Практическая часть

Видео:Теорема ПикаСкачать

Нахождение площади фигур геометрическим методом и по формуле Пика

Я решила убедиться в том, что формула Пика верна для всех рассмотренных примеров.

Оказывается, что если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.

Я рассмотрела некоторые задачи на клетчатой бумаге с клетками размером 1 см1 см и провела сравнительный анализ по решению задач (Таблица№1).

Таблица№1 Решение задач различными способами.

По формуле геометрии

По формуле Пика

Задача №1

S = 8 + 6/2 – 1 = 10 (см²)

Задача №2

S = 6 + 6/2 – 1 = 8 (см²)

Задача №3

S _кв =4 2 =16 см 2

S =16-(4,5+2*2)=7.5 см 2

S = 6 + 5/2 – 1 = 7,5 (см²)

Задача №4

S _пр =4 * 3=12 см 2

S = 5 + 7/2 – 1 = 7,5 (см²)

Задача № 5.[2]

S _пр =6 * 5=30 см 2

S = 12 + 6/2 – 1 = 14 (см²)

Задача №6.[2]

S = 12 + 17/2 – 1 = 19,5 (см²)

Задача №7.[4] Найдите площадь лесного массива (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м

S ₁ =(800*200)/2=80000 м 2

S ₂ =(200*600)/2=60000 м 2

Ответ: 420 000 м²

В = 8, Г = 7. S = 8 + 7/2 – 1 = 10,5 (см²)

1 см² — 200² м²; S = 40000 · 10,5 = 420 000 (м²)

Ответ: 420 000 м²

Задача №8 . Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе

1 см – 200 м.

S _кв =800 * 800=640000 м 2

Ответ: 320 000 м²

Решение. Найдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S = В + — 1

В = 7, Г = 4. S = 7 + 4/2 – 1 = 8 (см²)

1 см² — 200² м²; S = 40000 · 8 = 320 000 (м²)

Ответ: 320 000 м²

Задача №9 . Найдите площадь S сектора, считая стороны квадратных клеток равными 1. В ответе укажите .

Сектор является одной четвертой частью круга и, следовательно, его площадь равна одной четвертой площади круга. Площадь круга равна π R 2 , где R – радиус круга. В нашем случае R =√5 и, следовательно, площадь S сектора равна 5π/4. Откуда S /π=1,25.

Г= 5, В= 2, S = В + Г/2 – 1= 2 + 5/2 – 1= 3,5, ≈ 1,11

Задача №10. Найдите площадь S кольца, считая стороны квадратных клеток равными 1. В ответе укажите .

Площадь кольца равна разности площадей внешнего и внутреннего кругов. Радиус R внешнего круга равен

2 , радиус r внутреннего круга равен 2. Следовательно, площадь кольца равна 4 и, следовательно, . Ответ:4.

Г= 8, В= 8, S = В + Г/2 – 1= 8 + 8/2 – 1=11, ≈ 3,5

Выводы: Рассмотренные задания аналогичны заданию из вариантов контрольно-измерительных материалов ЕГЭ по математике (задачи №5,6),[7].

Из рассмотренных решений задач я увидела, что некоторые из них, например задачи № 2,6, легче решить, применяя геометрические формулы, так как высоту и основание можно определить по рисунку. Но в большинстве задач требуется разбиение фигуры на более простые (задача №7) или достраивание до прямоугольника (задачи №1,4,5), квадрата (задачи №3,8).

Из решения задач №9 и №10 я увидела, что применение формулы Пика к фигурам, которые не являются многоугольниками, даёт приближённый результат.

Для того, чтобы проверить рациональность применения формулы Пика, я провела исследование на предмет затраченного времени (Приложение 4, таблица №2).

Вывод: из таблицы и диаграммы (Приложение 4, диаграмма 1) видно, что при решении задач с помощью формулы Пика, времени затрачивается гораздо меньше.

Видео:Формула Пика в ЕГЭ и ОГЭ по математикеСкачать

Нахождение площади поверхности пространственных форм

Проверим применимость этой формулы к пространственным формам (Приложение 5, рисунок 4).

Найти площадь полной поверхности прямоугольного параллелепипеда, считая стороны квадратных клеток равными 1.

К сожалению, подсчитать количество узлов решетки, попавших на границу параллелепипеда и внутрь параллелепипеда нельзя. Поэтому вычислить площадь полной поверхности по формуле Пика невозможно.

Это недостаток формулы.

Видео:Квадратура круга: математически невозможная задача, оказавшаяся решаемойСкачать

Применение формулы Пика для нахождения площади территории

Решая задачи с практическим содержанием, (задачи №7,8; таблица №1), я решила применить данный способ для нахождения площади территории нашей школы, микрорайонов города Усть-Илимска, Иркутской области.

Ознакомившись с «Проектом границ земельного участка МАОУСОШ№11 г .Усть-Илимска» (Приложение 6),[1], я нашла площадь территории нашей школы и сравнила с площадью по проекту границ земельного участка (Приложение 9, таблица 3).

Рассмотрев карту правобережной части Усть-Илимска (Приложение 7),[8], я вычислила площади микрорайонов и сравнила с данными из «Генерального плана г. Усть-Илимска Иркутской области»[3]. Результаты представила в таблице (Приложение 9, таблица 4).

Рассмотрев карту Иркутской области (Приложение 7),[9], я нашла площадь территории и сравнила с данными из Википедии [10]. Результаты представила в таблице (Приложение 9, таблица 5).

Проанализировав результаты, я пришла к выводу: по формуле Пика эти площади можно найти гораздо проще, но результаты приблизительные.

Из проведенных исследований наиболее точное значение я получила при нахождении площади территории школы (Приложение 10, диаграмма 2). Большее расхождение в результатах получилось при нахождении площади Иркутской области (Приложение 10, диаграмма 3). Это связано с тем. Что не все границы области являются сторонами многоугольников, и вершины не являются узловыми точками.

Видео:Хитрая школьная задача ➜ Найдите площадь ➜ Формула ПИКА не РАБОТАЕТСкачать

Заключение

В результате моей работы я расширила свои знания о решении задач на клетчатой бумаге, определила для себя классификацию исследуемых задач.

При выполнении работы были решены задачи на нахождение площади многоугольников, изображённых на клетчатой бумаге двумя способами: геометрическим и с помощью формулы Пика.

Анализ решений и эксперимент по определению затраченного времени показал, что применение формулы даёт возможность решать задачи на нахождение площади многоугольника, более рационально. Это позволяет экономить время на ЕГЭ по математике.

Нахождение площади различных фигур, изображённых на клетчатой бумаге, позволило сделать вывод, что использование формулы Пика для вычисления площади кругового сектора и кольца нецелесообразно, так как она даёт приближённый результат, и, что формула Пика не применяется для решения задач в пространстве.

Так же в работе были найдены площади различных территорий по формуле Пика. Можно сделать вывод: использование формулы для нахождения площади различных территорий возможно, но результаты получаются приблизительными.

Выдвинутая мной гипотеза подтвердилась.

Я пришла к выводу, что тема, которая меня заинтересовала, достаточно многогранна, задачи на клетчатой бумаге многообразны, методы и приёмы их решения также разнообразны. Поэтому я решила продолжить работу в этом направлении.

Видео:Найдите площадь фигуры ★ 2 способа решения ★ Классический школьный способ ★ Формула ПИКАСкачать

Литература

Волков С.Д.. Проект границ земельного участка, 2008 г, с. 16.

Горина Л.В., Математика. Все для учителя, М:Наука, 2013 г.. №3, с. 28.

Прокопьева В.П., Петров А.Г., Генеральный план города Усть-Илимска Иркутской области, Госстрой России, 2004 г.. с. 65.

Рисс Е. А. , Жарковская Н. М. , Геометрия клетчатой бумаги. Формула Пика. — Москва, 2009, № 17, с. 24-25.

Смирнова И. М. ,. Смирнов В. А, Геометрия на клетчатой бумаге. – Москва, Чистые пруды, 2009, с. 120.

Смирнова И. М. , Смирнов В. А. , Геометрические задачи с практическим содержанием. – Москва, Чистые пруды, 2010, с. 150

Видео:9 Доказательство формулы ПикаСкачать

Площади многоугольников и тающий лёд

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Формула Пика

Как найти площадь многоугольника на клетчатой бумаге? Можно подсчитать число клеток, которые полностью накрыты фигурой, и ещё как-то учесть клетки, накрытые фигурой частично, — скажем, прибавить половину от числа этих клеток. И сказать, что площадь фигуры (в клеточках) приблизительно равна полученной сумме.

А можно вместо клеток, полностью или частично накрытых многоугольником, считать узлы сетки (вершины клеток) строго внутри многоугольника или на его границе.

Действительно, вокруг каждого узла сетки можно нарисовать по единичному квадратику. И если узел лежит на границе многоугольника, то этот квадратик накрыт многоугольником только частично. А если узел лежит внутри, то обычно и квадратик накрыт многоугольником полностью. впрочем, иногда всё же не полностью — но мы и считаем площадь только приближённо.

Но чудесным образом последний рецепт всегда даёт почти правильный ответ! А именно, верна Формула Пика. Площадь S многоугольника с вершинами в узлах сетки можно найти по формуле

где i — число узлов сетки строго внутри многоугольника, b — число узлов сетки на его границе.

Подчеркнём, что это уже не приближённая, а точная формула!

Интересно, что хотя длины сторон у многоугольников обычно совершенно не целые, формула Пика гарантирует, что площадь всегда получится целой или полуцелой.

Видео:Формула Пика в действии! Подписывайтесь, тогда узнаете другие секретные способы!Скачать

Тающий лёд

Формула Пика известна с XIX века, и с тех пор у неё появилось много доказательств, но большинство из них не такие уж простые. Мы обсудим предложенный в 1997 году швейцарским математиком Кристианом Блаттером мысленный эксперимент с тающим льдом, который сразу объясняет формулу Пика.

Поставим на каждый узел сетки по одинаковому цилиндрическому столбику изо льда. Каждый столбик очень тонкий (пересекается только с теми сторонами многоугольника, которые проходят через центр столбика) и весит 1 грамм.

Построим вокруг каждого столбика забор в виде единичного квадратика, после чего растопим весь лёд (во всех квадратиках вода растекается одинаково и симметрично относительно центра своего квадратика). Вся клетчатая плоскость будет равномерно залита водой, и в каждой ячейке площади 1 будет по 1 грамму воды. То есть количество воды в нашем многоугольнике (в граммах) будет равно его площади (в клетках).

С другой стороны, задумаемся, откуда эта вода попала в наш многоугольник. Посмотрим на какую-нибудь конкретную сторону многоугольника. Если через неё внутрь многоугольника втекла вода из какого-то столбика, то точно столько же воды из симметричного столбика (симметричного относительно середины этой стороны) через неё из многоугольника вытекло.

То есть внутри многоугольника ровно столько воды, сколько в нём было льда! А сколько в нём было льда? Каждый из узлов сетки внутри многоугольника даёт вклад 1 грамм, общий вес получается i граммов. Узлы на сторонах обычно дают по 1 2 грамма, но только если это не вершина, для вершины этот вес меньше — так что и общий вес узлов на границе получается не b 2 граммов, а меньше.

Насколько меньше? Продлим немного каждую сторону, обходя многоугольник вдоль сторон по часовой стрелке. На рисунке ниже красная часть дополняет каждую из синих частей до половины круга. Но красные части в сумме дают ровно один круг! Ведь, обходя многоугольник по контуру, мы в каждой вершине поворачиваемся на угол, соответствующий красной части, пока не вернёмся в исходную точку, сделав как раз полный оборот.

То есть суммарный вес льда внутри многоугольника равен i + b 2 − 1 , и мы получили формулу Пика!

Упражнение

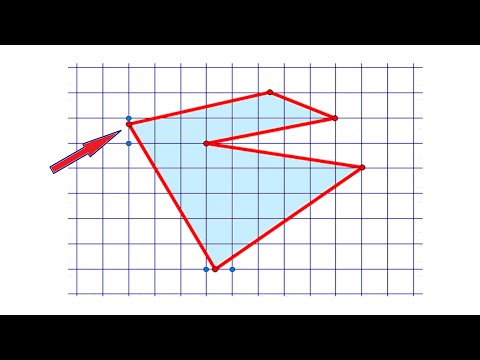
В рассуждении выше мы рисовали выпуклый многоугольник. А изменится ли что-то, если многоугольник станет невыпуклым? А если рассматривать «многоугольники с дырками»?

Видео:Топ 10 комментариев про формулу ПикаСкачать

Многоугольник. Формула Пика.

Возьмем невырожденный простой целочисленный многоугольник (значит он связный — две его произвольные точки могут быть объединены непрерывной кривой, целиком в нем содержащейся, и у всех его вершин целые координаты, его граница — связная ломаная без самопересечений, и у него не ненулевую площадь).

Для расчета площади такого многоугольника можно применить нижеследующую теорему открытую австрийским математиком Георгом Пиком в 1899 году.

Пусть N — число узлов внутри многоугольника, M — численность узлов на его границе, S— его площадь. Тогда применима Формула Пика:

Под «узлами» понимают пересечение линий.

Формула Пика нашла широкое применение для нахождения площади многоугольника построенного на листе в клетку. Масштаб клетки при этом равен 1 см 2 .

Вычислим площадь трапеции:

M = 24 (указаны красным цветом);

N = 25 (указаны синим цветом).

S= 24/2 + 25 -1 = 36 cм 2 .

Найдем площадь ниже представленного многоугольника:

🎥 Видео

Формула Пика для нахождении площади фигуры на клетчатом полеСкачать

Занятие 6. Площадь круга, формула Пика. Планиметрия для ЕГЭ и ОГЭСкачать

Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Формула ПикаСкачать