Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
«Соотношения отрезков в треугольнике:
Теорема Фалеса, теорема Менелая, правило масс»
провела: Громова Е.А
помогали: учащиеся 11А класса
г.о. Жуковский, 2018г.
Тип урока: урок с элементами бизнес игры.
Цель: провести обзор пройдённых теорем, актуализировать и обобщить знания учащихся по решению задач, с их использованием. Показать применение при решении задач ОГЭ и ЕГЭ.
Комментарий: урок проводится в форме бизнес игры, в которой учащиеся 11 класса проводят рекламную акцию по использованию теорем при решение задач на отношения отрезков в треугольнике.
Здравствуйте ребята, сегодняшний наш урок пройдет в нетрадиционной форме. Сегодня мы поиграем и помогут нам в этом (учитель представляет ведущих)
Задачи на соотношения, сложные задачи! И многие ученики не умеют или боятся их решать! Мы попробуем доказать, что эти задачи могут оказаться легкими, если знать приемы их решения. Теоремы о которых будет идти сегодня речь знаем, просто ребята обобщат наши знания, и мы посмотрим эти способы в сравнении.
А в конце урока проведем опрос: Кому какая теорема ближе, каждый из ребят попробует убедить вас, что именно его теорему надо применять!
2. Теорема Фалеса, обзор теории, примеры решения задач.
Представим вам традиционный способ решения данного вида задач, с помощью Теоремы Фалеса.
Теорема о пропорциональных отрезках
(Расширенная теорема Фалеса)
Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
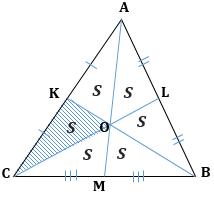
В треугольнике ABC на стороне ВС взята точка М так, что MB = МС, а на стороне АС взята точка К так, что АК = 3 КС. Отрезки ВК и АМ пересекаются в точке О. Найдите AO/OM
Решение. Обозначим длину отрезка КС через а, тогда АК = За. Проведём MP||ВК По теореме Фалеса КР = РС = а/2. По теореме о пропорциональных отрезках имеем:
Задача 2. (Решим быстро и устно)
На сторонах АВ и АС треугольника ABC взяты точки М и N, такие, что AM/MB = CN/NA = 1/2.
Отрезки BN и СМ пересекаются в точке К. Найти отношения отрезков BK/KN и CK/KM.
3. Теорема Менелая, обзор теории, примеры решения задач.
Представим Вам способ решения задач, с которым знакомят в профильном классе с помощью Теоремы Менелая.
Теорема: Теорема Менелая (ок. 100 г. н.э.). Пусть прямая пересекает треугольник ABC, причём C 1 – точка пересечения со стороной AB, A 1 – со стороной BC, B 1 – с продолжением стороны AC.
Тогда выполняется равенство:
В треугольнике АВС на стороне ВС взята точка N так, что NC = 3BN; на продолжении стороны АС за точку А взята точка М так, что МА = АС. Прямая MN пересекает сторону АВ в точке F. Найти отношение BF :FA
На сторонах AB и BC треугольника ABC взяты соответственно точки M и N так, что AM:MB=2:3, BN:NC=2:1. Отрезки AN и CM пересекаются в точке O. Найти отношение CO:OM.
4. Правило масс, обзор теории, примеры решения задач
Представим Вам совсем не традиционный способ, с которым вообще мало кто знаком, с помощью правила масс.
1. Пусть есть качели. Обозначим их в виде отрезка АВ и будем их считать невесомыми.(рис.1)
2. Причем, в точках А и В подвешены гирьки с массами m1 и m2. Для определенности будем считать, что m2>m1.(рис.2)
3. Задача найти в этом случае ту точку, которая уравновесит данные качели. Логично, что если эту точку поставить в середине отрезка, то m2 перевесит.(рис.3)
4. Центр масс данной системы двух точек будет такая точка О данного отрезка, что AO*m1 = BO*m2. Или соответственно: 
В треугольнике АВС проведены отрезки ВМ и АN так, что ВN: NC=1:5, а АМ: МС=1:2. Найти ВО:ОМ и АО:ON, где О — точка пересечения отрезков.
Помещаем в вершину С массу, равную единице. Поскольку точка М делит сторону АС в отношении 1:2, то по правилу рычага в точку А должна быть помещена масса, равная двум. Аналогично в точку В быть помещена масса, равная пяти, т. к. ВN: NC=1:5
1) 2А,5В,1С с центром масс в точке О.
2) 2A+1C=3M; 5В,3М — сист. Мат точек с ц. м. в т. О
По правилу рычага ВО:ОМ=3:5
3) 5В+1C=6N; 6N, 2А — сист. Мат точек с ц. м. в т. О
По правилу рычага АО:ОN=6:2=3:1
Ответ: ВО:ОМ=3:5, АО:ОN=6:2=3:1
Задача 6. ( ОГЭ. №26) (решают вместе с классом)
В треугольнике АВС из вершин А и В проведены отрезки АК и ВЕ, причем точки К и Е лежат на сторонах ВС и АС соответственно. Отрезки АК и ВЕ пересекаются в точке М так, что АМ : МК = 5, ВМ : МЕ = 2. Найдите отношения АЕ : ЕС и ВК : КС.
Поместим в точку А массу m,тогда по правилу рычага в точке К будет 5m из этого следует, что в точке М будет m+5m=6m.
Т.к. ВМ : МЕ = 2, то поместив некую массу m2 в т. В, то в Е получим 2m2, тогда в М 3m2, соответственно m2=2m, тогда в В будет 2m, а в Е 4m, тогда в С 4m-m=3m, тогда АЕ : ЕС= 3 и
5. Ну а теперь проверим какая теорема вам показалась более простая!
Задача 7.(решим самостоятельно, любым понравившимся вам способом)
На стороне ВС треугольника АВС взята точка D такая, что ВD : DC = 2:5, а на стороне АС точка Е такая, что 
Поверяем решение задачи.
5. Подведение итогов.
Опрос ребят, по выбору понравившейся теоремы.
Подсчет голосов, выбор победителя.
Итог: сегодня мы вспомнили все теоремы, порешали задачи, посмотрели, как их можно применять на экзаменах. Дома вы еще раз посмотрите и вспомните как решаются такие задачи.
№ 1 Задача на нахождение отношения на внутренних отрезках треугольника (тремя способами)
В треугольнике АВС точка М – середина АВ, точка N такая, что BN : NC = 3 : 2.
Прямая МN пересекает прямую АС в точке К. Найти отношение КС : АК.
№ 2. Задача на соотношения отрезков на сторонах треугольника (любым способом)
В треугольнике АВС отрезки AD и ВЕ, проведённые из вершин А и В к сторонам ВС и АС соответственно, делятся точкой пересечения Q в соотношении AQ : QD = 7 : 5, BQ : QE = 3 : 4.
В каков отношении точки D и Е делят сторону треугольника?
- Треугольник. Формулы и свойства треугольников.
- Типы треугольников
- По величине углов
- По числу равных сторон
- Вершины углы и стороны треугольника
- Свойства углов и сторон треугольника
- Теорема синусов
- Теорема косинусов
- Теорема о проекциях
- Формулы для вычисления длин сторон треугольника
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- Биссектрисы треугольника
- Свойства биссектрис треугольника:
- Формулы биссектрис треугольника
- Высоты треугольника
- Свойства высот треугольника
- Формулы высот треугольника
- Окружность вписанная в треугольник
- Свойства окружности вписанной в треугольник
- Формулы радиуса окружности вписанной в треугольник
- Окружность описанная вокруг треугольника
- Свойства окружности описанной вокруг треугольника
- Формулы радиуса окружности описанной вокруг треугольника
- Связь между вписанной и описанной окружностями треугольника
- Средняя линия треугольника
- Свойства средней линии треугольника
- Периметр треугольника
- Формулы площади треугольника
- Формула Герона
- Равенство треугольников
- Признаки равенства треугольников
- Первый признак равенства треугольников — по двум сторонам и углу между ними
- Второй признак равенства треугольников — по стороне и двум прилежащим углам
- Третий признак равенства треугольников — по трем сторонам
- Подобие треугольников
- Признаки подобия треугольников
- Первый признак подобия треугольников
- Второй признак подобия треугольников
- Третий признак подобия треугольников
- 51. Планиметрия Читать 0 мин.
- 51.506. Отношения
- 💡 Видео
Видео:Задача про соотношение сторон. Геометрия 7 класс.Скачать

Треугольник. Формулы и свойства треугольников.
Видео:Найдите отношение отрезковСкачать

Типы треугольников
По величине углов
По числу равных сторон
Видео:Найдите отношение отрезков диагоналиСкачать

Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 bc · cos α
b 2 = a 2 + c 2 — 2 ac · cos β
c 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Видео:Отношение длин отрезковСкачать

Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 — a 2
mb = 1 2 √ 2 a 2 +2 c 2 — b 2
mc = 1 2 √ 2 a 2 +2 b 2 — c 2
Видео:8 класс, 19 урок, Пропорциональные отрезкиСкачать

Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p — a ) b + c
lb = 2√ acp ( p — b ) a + c
lc = 2√ abp ( p — c ) a + b
где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Видео:2. Соизмеримые и несоизмеримые отрезки. Алексей Савватеев. 100 уроков математики - 6 - 7 классСкачать

Связь между вписанной и описанной окружностями треугольника
Видео:Нахождение стороны прямоугольного треугольникаСкачать

Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Видео:№533. Найдите отношение отрезков АВ и CD, если их длины равны соответственно 15 см и 20 см.Скачать

Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Видео:Найти отношение отрезков, на которые высота треугольника делит сторону | Геометрия ОГЭ Геометрия ЕГЭСкачать

Формулы площади треугольника
Формула Герона
| S = | a · b · с |
| 4R |
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Видео:Теорема Менелая | Математика | TutorOnlineСкачать

Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:8 класс, 20 урок, Определение подобных треугольниковСкачать

51. Планиметрия  Читать 0 мин.
Читать 0 мин.
Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

51.506. Отношения
Зачастую в геометрических задачах в условии даются отношения отрезков и площадей или отношение отрезков нужно найти. Существует ряд теорем и свойств фигур и их элементов, в которых так или иначе используются отношения.
ОТНОШЕНИЯ ОТРЕЗКОВ:
1. Все медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2 к 1, считая от вершины: AO : AM = 2 : 1.
2. Средняя линия треугольника равна половине основания: $MN = fracBC$
3. Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна ее половине $CM = fracAB$
4. Диагонали параллелограмма точкой пересечения делятся пополам.
Произвольный параллелограмм или ромб:
Прямоугольник или квадрат:
ОТНОШЕНИЯ ПЛОЩАДЕЙ:
1. Медиана разбивает треугольник на два равновеликих (по площади) треугольника: $S_ = S_ = S$
2. Треугольник делится тремя медианами на шесть равновеликих треугольников:
3. Если площадь треугольника равна S, то площадь треугольника, составленного из его медиан, равна $fracS$
ЛЕММЫ О ПЛОЩАДЯХ ТРЕУГОЛЬНИКА:
Площади подобных фигур относятся как квадрат коэффициента подобия.
Если стороны треугольников с общей вершиной лежат на одной прямой, то их площади относятся как основания.
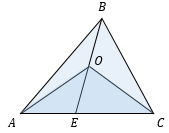
Если два треугольника имеют общую сторону, то их площади соотносятся как длины отрезков BE и OE.
Если два треугольника имеют общий угол, то их площади соотносятся как произведения соответствующих сторон, прилежащих к этому углу.
Лемма 4 применима даже в том случае, если точки нового треугольника были взяты не на сторонах, а на продолжениях сторон. Пусть точка Е лежит на продолжении стороны AB за вершину В.
💡 Видео
Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Задачи на даче-2. Тригонометрия в лесу. Теорема об отношении отрезков треугольникаСкачать

Математика | Метрические соотношения в прямоугольном треугольникеСкачать

Геометрия 7 класс, подготовка к ОГЭ, ЕГЭ. Отношение отрезков.Скачать

























 Читать 0 мин.
Читать 0 мин.