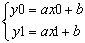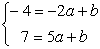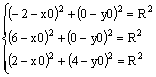Интегральное исчисление.Нахождение площадей фигур в среде Mathcad Преподаватель математики: Шутилина С.Н.
Площадь фигуры Для нахождения площади фигуры, ограниченной кривыми, используется определенный интеграл. При этом, пределы интегрирования находятся в точках пересечения заданных кривых
Работа в Mathcad В среде Mathcad для определения пределов интегрирования используется функция root(f(x),x), а для нахождения определенного интеграла – соответствующий шаблон на наборной панели Calculus
Формулировка задания Найти площадь фигуры, ограниченной кривыми:
Реализация в среде Mathcad Для определения пределов интегрирования необходимо будет построить графики обеих функций, графически определить приближенные значения, а потом, используя функцию root(f(x),x), найти точные значения пределов интегрирования Для построения графиков функций, обозначим одну функцию за f(x), а вторую за y(x)
Реализация в среде Mathcad Зададим обе функции:
Реализация в среде Mathcad Построим графики этих функций:
Реализация в среде Mathcad По графику определилась фигура, площадь которой нужно найти: Зададим эту новую функцию в Mathcad
Реализация в среде Mathcad Также графически определились приближенные пределы интегрирования Зададим приближенное значение нижнего предела интегрирования:
Реализация в среде Mathcad Точное значение нижнего предела интегрирования найдем с помощью функции root. Будем учитывать, что вместо f(x), в функции root используется g(x):
Реализация в среде Mathcad Зададим приближенное значение верхнего предела интегрирования и найдем его точное значение:
Реализация в среде Mathcad Теперь можно найти значение интеграла фигуры g(x), ограниченной линиями f(x) и y(x):
Выводы Среда Mathcad упрощает решение сложных математических задач и позволяет использовать на занятиях по математике не только традиционные методы, но и компьютерную технику, которая облегчает вычисления. Однако, существенным недостатком решения задач с помощью Mathcad является то, что среда выводит только конечный результат, поэтому промежуточные вычисления не видны пользователю
- Интегральное исчисление. Нахождение площадей фигур в среде Mathcad
- Описание презентации по отдельным слайдам:
- Охрана труда
- Библиотечно-библиографические и информационные знания в педагогическом процессе
- Охрана труда
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Определение площадей фигур, ограниченных непрерывными линиями
- 📹 Видео
Видео:MathCad вычисление площади треугольника.wmvСкачать

Интегральное исчисление. Нахождение площадей фигур в среде Mathcad
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Интегральное исчисление.
Нахождение площадей фигур в среде Mathcad
Преподаватель математики: Шутилина С.Н.
Площадь фигуры
Для нахождения площади фигуры, ограниченной кривыми, используется определенный интеграл. При этом, пределы интегрирования находятся в точках пересечения заданных кривых
Работа в Mathcad
В среде Mathcad для определения пределов интегрирования используется функция root(f(x),x), а для нахождения определенного интеграла – соответствующий шаблон на наборной панели Calculus
Формулировка задания
Найти площадь фигуры, ограниченной кривыми:
Реализация в среде Mathcad
Для определения пределов интегрирования необходимо будет построить графики обеих функций, графически определить приближенные значения, а потом, используя функцию root(f(x),x), найти точные значения пределов интегрирования
Для построения графиков функций, обозначим одну функцию за f(x), а вторую за y(x)
Реализация в среде Mathcad
Зададим обе функции:
Реализация в среде Mathcad
Построим графики этих функций:
Реализация в среде Mathcad
По графику определилась фигура, площадь которой нужно найти:
Зададим эту новую функцию в Mathcad
Реализация в среде Mathcad
Также графически определились приближенные пределы интегрирования
Зададим приближенное значение нижнего предела интегрирования:
Реализация в среде Mathcad
Точное значение нижнего предела интегрирования найдем с помощью функции root.
Будем учитывать, что вместо f(x), в функции root используется g(x):
Реализация в среде Mathcad
Зададим приближенное значение верхнего предела интегрирования и найдем его точное значение:
Реализация в среде Mathcad
Теперь можно найти значение интеграла фигуры g(x), ограниченной линиями f(x) и y(x):
Выводы
Среда Mathcad упрощает решение сложных математических задач и позволяет использовать на занятиях по математике не только традиционные методы, но и компьютерную технику, которая облегчает вычисления.
Однако, существенным недостатком решения задач с помощью Mathcad является то, что среда выводит только конечный результат, поэтому промежуточные вычисления не видны пользователю
Курс повышения квалификации
Охрана труда
- Сейчас обучается 100 человек из 43 регионов
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
- Сейчас обучается 351 человек из 64 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 217 человек из 54 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 540 407 материалов в базе
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 31.12.2020
- 4220
- 3
- 31.12.2020
- 4223
- 0
- 10.12.2020
- 4337
- 0
- 08.12.2020
- 4282
- 0
- 05.12.2020
- 4080
- 0
- 18.10.2020
- 4108
- 0
- 04.08.2020
- 4649
- 0
- 26.07.2020
- 3766
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 13.02.2020 181
- PPTX 1.6 мбайт
- 0 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Цветкова Анна Сергеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 1 год и 1 месяц
- Подписчики: 0
- Всего просмотров: 23785
- Всего материалов: 237
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Омской области школы и колледжи перейдут на дистанционное обучение с 7 по 21 февраля
Время чтения: 1 минута
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
В России классы будут переводить на дистант, если заболели 20% детей
Время чтения: 1 минута
Новые курсы: школьные службы примирения, детская журналистика и другие
Время чтения: 15 минут
Онлайн-семинар о развитии управляющих функций мозга ребенка
Время чтения: 1 минута
Пермский Роспотребнадзор предписал перевести обучение в школах и ссузах на дистант
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Определение площадей фигур, ограниченных непрерывными линиями
8.2 Определение площадей фигур, ограниченных непрерывными линиями
Площадь криволинейной трапеции, ограниченной графиком функции f(x), отрезком [a,b] на оси Ox и двумя вертикалями х = а и х = b, a 2 и y = 0.
Рис. 6.5. Нахождение площади фигуры, ограниченной линиями f(x) = 1 – x 2 и y = 0
Площадь фигуры, заключенной между графиками функций f1(x) и f2(x)и прямыми х = а и х = b, вычисляется по формуле:
Внимание. Чтобы избежать ошибок при вычислении площади, разность функций надо брать по модулю. Таким образом, площадь будет всегда положительной величиной.
Пример. Нахождение площади фигуры, ограниченной линиями 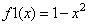
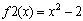
1. Строим график функций.
2. Находим точки пересечения функций с помощью функции root. Начальные приближения определим по графику.
3. Найденные значения x подставляем в формулу 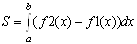
8.3 Построение кривых по заданным точкам
Построение прямой, проходящей через две заданные точки
Для составления уравнения прямой, проходящей через две точки А(x0,y0) и B(x1,y1), предлагается следующий алгоритм:
1. Прямая задается уравнением y = ax + b,
где a и b — коэффициенты прямой, которые нам требуется найти.
Подставляем в это уравнение заданные координаты точек и получаем систему:
2. Данная система является линейной. В ней две неизвестные переменные: a и b. Систему можно решить матричным способом.
Пример. Построение прямой, проходящей через точки А(–2,–4) и В(5,7).
Подставим в уравнение прямой координаты данных точек и получим систему:
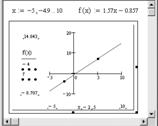
Решение этой системы в MathCAD представлено на рисунке 6.7.
Рис. 6.7.Решение системы
В результате решения системы получаем: а = 1.57, b = –0.857. Значит, уравнение прямой будет иметь вид: y = 1.57x – 0.857. Построим эту прямую (рис. 6.8).
Рис. 6.8. Построение прямой
Построение параболы, проходящей через три заданные точки
Для построения параболы, проходящей через три точки А(x0,y0), B(x1,y1) и C(x2,y2), алгоритм следующий:
1. Парабола задается уравнением
y = ax 2 + bх + с, где
а, b и с — коэффициенты параболы, которые нам требуется найти.
Подставляем в это уравнение заданные координаты точек и получаем систему:
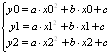
2. Данная система является линейной. В ней три неизвестные переменные: a, b и с. Систему можно решить матричным способом.
3. Полученные коэффициенты подставляем в уравнение и строим параболу.
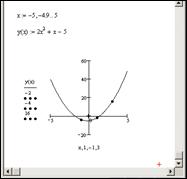
Пример. Построение параболы, проходящей через точки А(–1,–4), B(1,–2) и C(3,16).
Подставляем в уравнение параболы заданные координаты точек и получаем систему:
Решение этой системы уравнений в MathCAD представлено на рисунке 6.9.
Рис. 6.9. Решение системы уравнений
В результате получены коэффициенты: a = 2, b = 1, c = –5. Получаем уравнение параболы: 2x 2 +x –5 = y. Построим эту параболу (рис. 6.10).
Рис. 6.10. Построение параболы
Построение окружности, проходящей через три заданные точки
Для построения окружности, проходящей через три точки А(x1,y1), B(x2,y2) и C(x3,y3), можно воспользоваться следующим алгоритмом:
1. Окружность задается уравнением
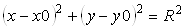
где x0,y0 — координаты центра окружности;
R — радиус окружности.
2. Подставим в уравнение окружности заданные координаты точек и получим систему:

Данная система является нелинейной. В ней три неизвестные переменные: x0, y0 и R. Система решается с применением вычислительного блока Given – Find.
Пример. Построение окружности, проходящей через три точки А(–2,0), B(6,0) и C(2,4).
Подставим в уравнение окружности заданные координаты точек и получим систему:
Решение системы в MathCAD представлено на рисунке 6.11.
Рис. 6.11. Решение системы
В результате решения системы получено: x0 = 2, y0 = 0, R = 4. Подставим полученные координаты центра окружности и радиус в уравнение окружности. Получим: 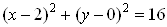
📹 Видео
Площадь треугольника, построенного на векторахСкачать

Как найти площадь треугольника без формулы?Скачать

Математика это не ИсламСкачать

Найти площадь треугольника АВС. Задачи по рисункамСкачать

Запомни: все формулы для площади треугольникаСкачать

Как найти площадь треугольника, зная координаты его вершины.Скачать

Как найти площадь этого треугольника, не зная формулы?Скачать

Найти площадь треугольника на векторахСкачать
Площади треугольникаСкачать
8 класс, 14 урок, Площадь треугольникаСкачать

Найдите площадь треугольника изображенного на клетчатой бумаге с размером клетки 1х1 см.Скачать

👉 ФОРМУЛА ГЕРОНА. Площадь треугольника #shortsСкачать

Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?Скачать

Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать