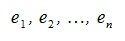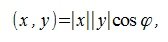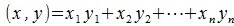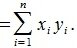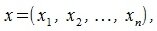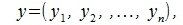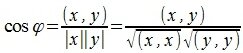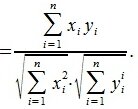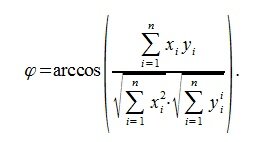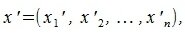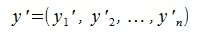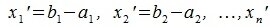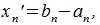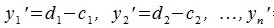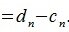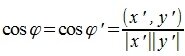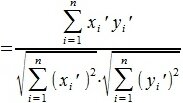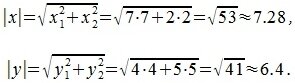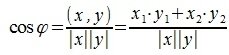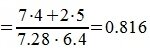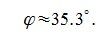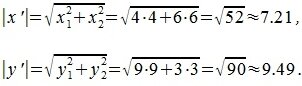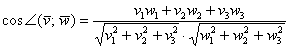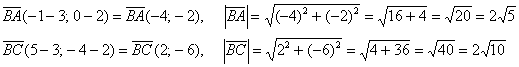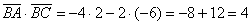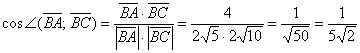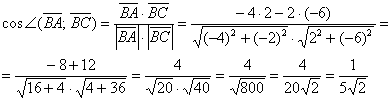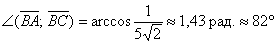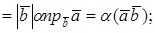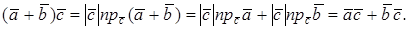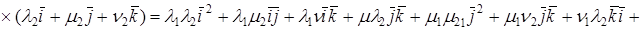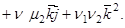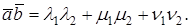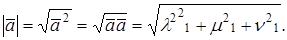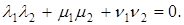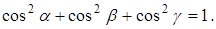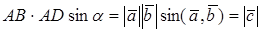Пусть в n-мерном пространстве задан ортонормированный базис
Как известно скалярное произведение ненулевых векторов x и y называется произведение
Если x=0 или y=0, то скалярное произведение равно нулю.
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
Так как рассматривается пространство с ортонормированным базисом, то скалярное произведение можно вычислить также из выражения
координаты векторов x и y соответственно.
Из выражений (1) и (2) следует, что косинус угла между двумя векторами равен
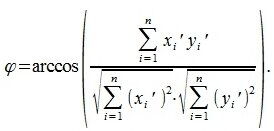
И, следовательно, угол между двумя векторами будет равен
Вариант 2. Начальные точки векторов произвольные.
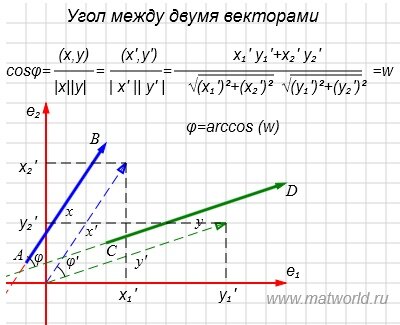
Пусть заданы векторы x= AB и y= CD, где 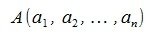
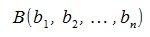
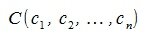
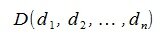
Переместим параллельно векторы x и y так, чтобы начальные точки векторов совпали с началом координат. Получим векторы x’ и y’ с координатами (т.е. с конечными точками):
При таком перемещении угол между векторами x и y равен углу между векторами x’ и y’. Следовательно косинус угла между двумя векторами равен:
Угол между двумя векторами будет равен:
Видео:Угол между векторами. 9 класс.Скачать

Примеры вычисления угла между двумя векторами
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
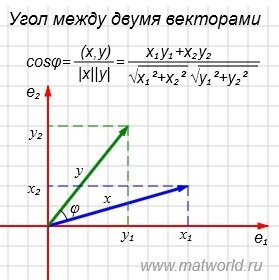
Пример . Найти угол между векторами x=(7,2) и y=(4,5).
На рисунке Рис. 1 в двухмерном пространстве представлены векторы x=(7,2) и y=(4,5).
Для вычисления угла между векторами x и y, вычислим нормы векторов x и y:
Косинус угла между векторами x и y, будет равен:
Из выражения (5) вычисляем угол φ:
Вариант 2. Начальные точки векторов произвольные.
Пример . Найти угол между векторами x= AB и y= CD, где A(-1,1), B(3, 7), C(3,2), D(12,5).
На рисунке Рис. 2 в двухмерном пространстве представлены векторы x= AB и y= CD.
Переместим параллельно векторы x и y так, чтобы начальные точки векторов совпали с началом координат. Получим векторы x’ и y’ с координатами (т.е. с конечными точками): x’=(3-(-1),7-1)=(4,6), y’=(12-3,5-2)=(9,3).
Угол φ между векторами x и y равен углу φ’ между векторами x’ и y’. Поэтому вычисляя угол φ’ , получим угол между векторами x и y.
Вычислим норму векторов x’ и y’:
Косинус угла между векторами x’ и y’:
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

1.6.9. Как найти угол между векторами в координатах?
Теперь у нас есть полная информация, чтобы ранее выведенную формулу косинуса угла между векторами 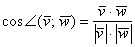
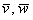
Косинус угла между векторами плоскости 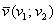
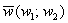
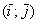
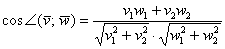
Косинус угла между векторами пространства 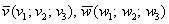
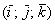
Возвращаемся к нашим треугольникам:
Задача 31
Даны три вершины треугольника 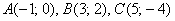
Решение: по условию чертёж выполнять не требуется, но всё-таки: 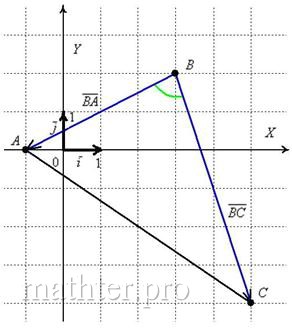
Из чертежа совершенно очевидно, что угол 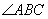
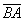
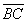
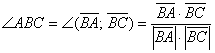
Вычислим скалярное произведение:
Таким образом:
Именно такой порядок выполнения задания рекомендую «чайникам». Более подготовленные читатели могут записать вычисления «одной строкой»:
Косинус получился «плохим» (не табличным), однако, это не окончательный ответ задачи, и поэтому, к слову, не имеет особого смысла избавляться от корня в знаменателе.
Найдём сам угол:
Если посмотреть на чертёж, то результат вполне правдоподобен. Для проверки можно использовать Алгебраический Калькулятор (см. Приложения) или даже измерить угол транспортиром (у кого он есть). Только не повредите покрытие монитора =)
Ответ: 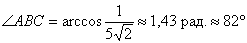
В ответе не забываем, что спрашивалось про угол треугольника (а не про угол между векторами), не забываем указать точный ответ: 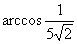
Задача 32
В пространстве задан треугольник координатами своих вершин 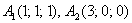
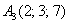
Это пример для самостоятельного решения, и, конечно же, задачка творческая, повторяем взаимосвязь между углом и знаком скалярного произведения:
Задача 33
При каком значении 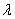
Решение и ответ в конце книги.
Следующий небольшой параграф будет посвящен ортогональным проекциям векторов, в которых тоже «замешано» скалярное произведение:
Видео:Угол между векторами | МатематикаСкачать

УГОЛ МЕЖДУ ВЕКТОРАМИ В ОРТОНОРМИРОВАННОМ БАЗИСЕ
ДОКАЗАТЕЛЬСТВО СВОЙСТВ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ
Свойство первое следует из определения скалярного произведения: 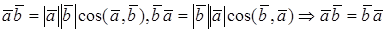
Второе и третье свойства следуют из линейных свойств проекции вектора на ось (направление): 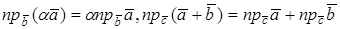
СКАЛЯРНЫЙ КВАДРАТ
Скалярным квадратом называется скалярное произведение 
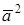
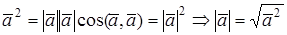
УГОЛ МЕЖДУ ВЕКТОРАМИ
Из определения 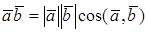
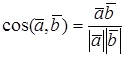
УСЛОВИЕ ОРТОГОНАЛЬНОСТИ ДВУХ ВЕКТОРОВ
Теорема. Векторы 

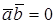
Доказательство необходимости. Пусть 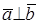
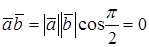

Доказательство достаточности. Пусть 
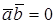
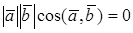
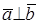
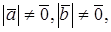
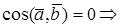
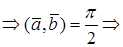
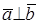
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ В ОРТОНОРМИРОВАННОМ БАЗИСЕ
Теорема. В ортонормированном базисе скалярное произведение векторов 

Доказательство. Пусть в пространстве выбран ортонормированный базис 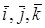


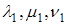

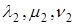
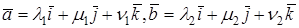
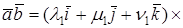
Так как 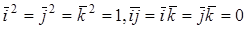
МОДУЛЬ ВЕКТОРА В ОРТОНОРМИРОВАННОМ БАЗИСЕ
Из формулы для скалярного произведения при 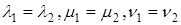
УГОЛ МЕЖДУ ВЕКТОРАМИ В ОРТОНОРМИРОВАННОМ БАЗИСЕ
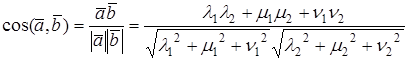
УСЛОВИЕ ОРТОГОНАЛЬНОСТИ ДВУХ ВЕКТОРОВ В
Если 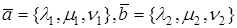
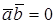
НАПРАВЛЯЮЩИЕ КОСИНУСЫ ВЕКТОРА
Определение. Направляющими косинусами вектора 

Пусть 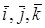
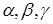

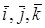
Направляющими косинусами вектора 

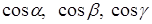
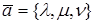
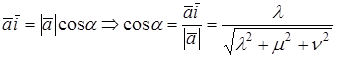
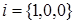
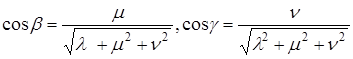
Замечание. Для любого вектора 
ЛИНЕЙНЫЕ СВОЙСТВА ПРОЕКЦИИ ВЕКТОРА НА ОСЬ
В ортонормированном базисе координаты вектора равны проекциям этого вектора на направления соответствующих базисных векторов.
Действительно, если 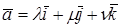
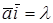
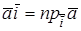
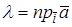
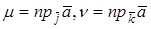
Если 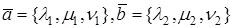
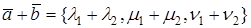
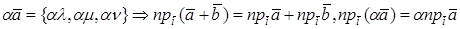
1. Дайте определение скалярного произведения векторов.
2. Выведите условие ортогональности двух векторов.
3. Докажите формулу скалярного произведения векторов в ортогональном базисе.
4. Напишите формулу модуля вектора в ортонормированном базисе.
5. Выведите условие ортогональности двух векторов в ортогональном базисе.
§6. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Векторным произведением вектора 

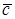
1. 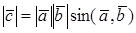
2. 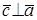
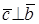
3. Упорядоченная тройка векторов 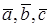
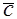
Векторное произведение 

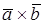
 D C D C 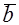 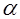 A A 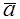 B Рис. 15. B Рис. 15. | 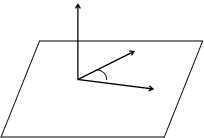 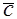   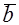 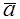  Рис. 14. Рис. 14. |
Замечания. 1. Модуль 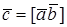


Векторы 

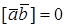
СВОЙСТВА ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
1. 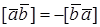
2. 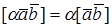
3. 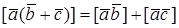
Это свойство примем без доказательства.
ДОКАЗАТЕЛЬСТВО СВОЙСТВ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
1. Пусть 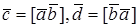
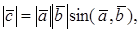
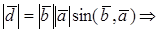
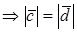
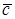
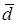


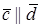
По определению с конца вектора 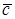


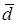


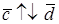
Следовательно, имеем, что 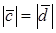
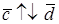
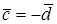
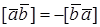
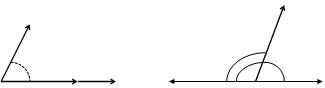 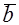 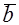 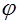 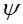 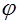 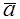 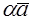 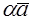 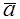 Рис. 16. Рис. 16. |
2. Пусть 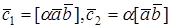
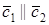
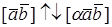
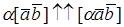
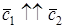
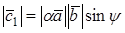
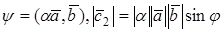
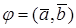
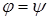
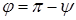
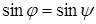
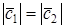
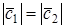
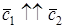
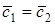
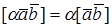
💥 Видео
100 тренировочных задач #135 Угол между векторамиСкачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Как находить угол между векторамиСкачать

105. Угол между векторамиСкачать

Угол между векторамиСкачать

11 класс, 5 урок, Угол между векторамиСкачать

найти угол между единичными векторамиСкачать

Нахождение угла между векторами через координаты. 9 класс.Скачать

Угол между векторами. Уроки 11. Геометрия 9 классСкачать

Как разложить вектор по базису - bezbotvyСкачать

9 класс, 17 урок, Угол между векторамиСкачать

Коллинеарность векторовСкачать

§48 Ортонормированный базис евклидова пространстваСкачать

Геометрия 9 класс (Урок№18 - Угол между векторами. Скалярное произведение векторов.)Скачать

Угол между векторамиСкачать