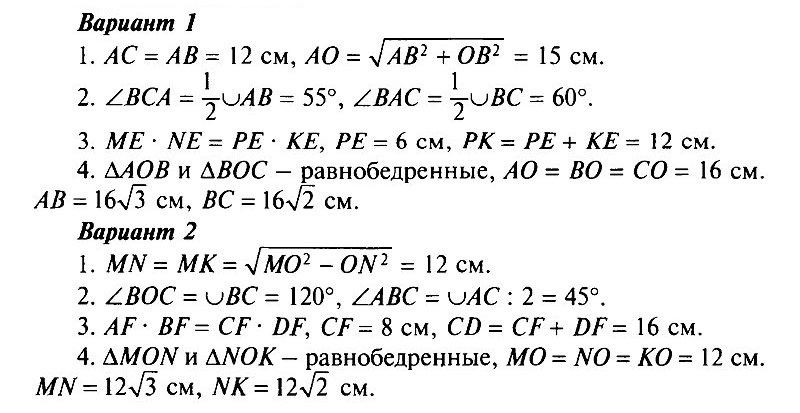Зачет по геометрии окружность атанасян

12 карточек по 10 вопросов по теме «Окружность» по учебнику Л. С. Атанасян, В. Ф. Бутузов и др.

Видео:ВСЯ ГЕОМЕТРИЯ 8 КЛАСС ЗА 15 МИНУТ / АТАНАСЯН / К ОГЭСкачать

Скачать:

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Предварительный просмотр:

Зачёт по теме: «Окружность».

1. Что называется серединным перпендикуляром?
2. Сколько окружностей можно вписать в треугольник и в какой?
3. Где в треугольнике находиться центр вписанной окружности?
4. Теорема о серединном перпендикуляре.
5. Теорема о высотах треугольника.
6. Сколько окружностей можно описать около треугольника и около какого?
7. Какая дуга называется полуокружностью?
8. Определение касательной.
9. Теорема о касательной.
10. Какой угол называется вписанным?

1. Теорема о биссектрисе.
2. Определение полуокружности.
3. Как измеряется центральный угол?
4. Теорема о серединном перпендикуляре.
5. Определение описанной окружности.
6. Определение вписанной окружности.
7. Взаимное расположение прямой и окружности.
8. Определение касательной.
9. Теорема о двух пересекающихся хордах.
10. Теорема об отрезках касательных.

1. Какая прямая называется секущей?
2. Теорема о серединном перпендикуляре.
3. Какой угол называется центральным?
4. Как через данную точку окружности провести касательную к этой окружности?
5. Как измеряется вписанный угол?
6. Следствие об углах, опирающихся на полуокружность.
7. Теорема о высотах треугольника.
8. Теорема о вписанной окружности.
9. Какая окружность называется описанной ?
10. Замечания по описанной окружности.

1. Какая прямая называется касательной?
2. Теорема об отрезках касательных.
3. Какая окружность называется вписанной?
4. Теорема и замечания об описанной окружности.
5. Какая дуга больше полуокружности?
6. Что называется полуокружностью?
7. Как измеряется вписанный угол?
8. Теорема о биссектрисе.
9. Теорема о серединном перпендикуляре.
10. Теорема о высотах треугольника.

1. Взаимное расположение прямой и окружности.
2. Теорема о касательной.
3. Какой угол называется центральным?
4. Как определяется градусная мера дуги?
5. Следствие об углах, опирающихся на одну и ту же дугу?
6. Что называется серединным перпендикуляром?
7. Теорема о биссектрисе.
8. Теорема о вписанной окружности
9. Каким свойством обладают стороны четырёхугольника, описанного около окружности?
10. Сколько окружностей можно вписать в треугольник и в какой?

1. Какая прямая называется секущей?
2. Теорема о касательной.
3. Какой угол называется центральным?
4. Что называется полуокружностью?
5. Следствие вписанных углов, опирающихся на одну и ту же дугу.
6. Теорема об отрезках пересекающихся хорд.
7. Теорема о биссектрисе.
8. Теорема о высотах треугольника.
9. Замечания о вписанной окружности.
10. Замечания об описанной окружности.

1. Какой угол называется вписанным?
2. Какая прямая называется касательной? Что такое точка касания?
3. Какой угол называется центральным?
4. Теорема об отрезках пересекающихся хорд.
5. Определение серединного перпендикуляра.
6. Теорема о серединном перпендикуляре.
7. Какая окружность называется вписанной?
8. Каким свойством обладают стороны четырёхугольника, описанного около окружности?
9. Теорема об описанной окружности.
10. Каким свойствам обладают углы четырёхугольника, вписанного в окружность?

1. определение секущей. Определение касательной.
2. Теорема об отрезках касательных.
3. Какая дуга меньше полуокружности, какая больше?
4. Какой угол называется вписанным и как он измеряется?
5. Следствия о вписанных углах.
6. Теорема и следствия о биссектрисе.
7. Какая окружность называется вписанной в многоугольник?
8. Определение серединного перпендикуляра.
9. Какая окружность называется описанной около многоугольника?
10. Каким свойством обладают стороны четырёхугольника, описанного около окружности?

1. Взаимное расположение прямой и окружности.
2. Определение полуокружности.
3. Какой угол называется центральным, как он измеряется?
4. Какой угол называется вписанным, как он измеряется?
5. Определение серединного перпендикуляра.
6. Теорема о касательной.
7. Какая окружность называется описанной?
8. Сколько треугольников и каких можно вписать в треугольник?
9. Теорема о высотах треугольника.
10. Следствия вписанных углов.

1. Теорема о касательной.
2. Следствие вписанного угла, опирающегося на полуокружность.
3. Определение полуокружности.
4. Как через данную точку окружности провести касательную к этой окружности?
5. Теорема об отрезках пересекающихся хорд.
6. Определение серединного перпендикуляра.
7. Теорема о биссектрисе.
8. Определение описанной окружности.
9. Теорема о вписанной окружности.
10. Каким свойством обладают углы четырёхугольника, вписанного в окружность?

1. Каким свойствам обладают стороны четырёхугольника, описанного около окружности?
2. Определение вписанной окружности.
3. Теорема об описанной окружности.
4. Определение полуокружности.
5. Как измеряется вписанный угол?
6. Определение центрального угла.
7. Теорема о серединном перпендикуляре.
8. Теорема о высотах треугольника.
9. Взаимное расположение прямой и окружности.
10. Определение секущей.

1. Теорема о касательной.
2. Теорема об отрезках касательных.
3. Теорема о биссектрисе.
4. Теорема о серединном перпендикуляре.
5. Теорема о высотах треугольника.
6. Теорема об отрезках пересекающихся хорд.
7. Теорема о вписанной окружности.
8. Теорема об описанной окружности.
9. Определение касательной.
10. Как измеряется вписанный угол?

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

По теме: методические разработки, презентации и конспекты

Зачёт по геометрии. Тема:»Метод координат». 9 класс

В данном зачёте учащимся предлагается ответить на 15 вопросов по теме «Метод координат», ответы на которые позволят сделать учителю вывод об уровне усвоения темы.

Зачёт по геометрии. Тема»»Метод координат». 11 класс.

В зачёте учащимся предлагается ответить на вопросы, касающиеся теоретической части темы «Метод координат».

Зачёт по геометрии «Длина окружности и площадь круга», 9 класс

Для организации зачёта по теме «Длина окружности и площадь круга» приводятся вопросы для подготовки к зачёту и лист для письменного опроса.

Зачёт по геометрии. Тема «Многоугольники». 8 класс

Представленный материал помогает организовать зачёт по теме «Многоугольники. Четырёхугольники» в 8 классе. Здесь вы можете найти вопросы для подготовки к зачёту и листы с двумя видами контроля з.

Билеты к зачёту по геометрии в 8 классе по теме:»Четырёхугольники»

Для проведения зачёта разработанны билеты по геометрии.

карточки к зачёту по геометрии 10-11 кл

карточки к зачёту по геометрии 10-11 кл.

Самостоятельная работа к зачёту по геометрии 8 класс

Самостоятельная работа к зачёту по геометрии 8 класс.

Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Зачет по теме «Окружность» , геометрия 8 класс

Видео:Бестселлер Все правила по геометрии за 7 классСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Зачет по теме «Окружность», 8 класс

(Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. «Геометрия, 8»)

1. Прямая и окружность имеют две общие точки, если расстояние от … до … меньше …

2. Если прямая АВ – касательная к окружности с центром О и В – точка касания, то прямая АВ и … ОВ …

3. Угол АОВ является центральным, если точка О является … лучи ОА и ОВ …

4. Вписанный угол, опирающийся на диаметр, …

5. Рис.1. ABD = … AOD = …

6. Рис.2. Если хорды АВ и CD окружности пересекаются в точке Е, то верно равенство …

7. Рис.3. Если АВ – касательная, AD – секущая, то выполняется равенство …

8. Если четырехугольник ABCD вписан в окружность, то …

9. Центр окружности, вписанной в треугольник, совпадает с точкой …

10. Если точка А равноудалена от сторон данного угла, то она лежит на …

11. Если точка В лежит на серединном перпендикуляре, проведенному к данному отрезку, то она …

12. Около любого … можно описать окружность.

1. Прямая и окружность имеют только одну общую точку, если расстояние от … до … равно …

2. Если прямая CD проходит через конец радиуса ОК и CD ┴ ОК, то CD является … к данной окружности.

3. Угол АВС является вписанным, если точка В …, лучи ВА и ВС …

4. Вписанные углы равны, если они … на одну …

5. Рис.1. ABD = … A С D = …

6. Рис.2. Если отрезки АВ и А C – отрезки касательных к окружности, проведенных из одной точки, то…

7. Рис.3. Если АС и A Е – секущие, то выполняется равенство …

8. Если четырехугольник описан около окружности, то …

9. Центр окружности, описанной около треугольника, совпадает с точкой …

10. Если точка С равноудалена от концов данного отрезка, то она лежит на …

11. Если точка D лежит на биссектрисе данного угла, то она …

12. В любой … можно вписать окружность.

Видео:КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

Дистанционные курсы для педагогов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 929 человек из 80 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 321 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 701 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

• Талонина Татьяна ПетровнаНаписать 3567 01.11.2018

Номер материала: ДБ-193976

29.10.2018 140

16.09.2018 417

16.09.2018 4273

05.08.2018 629

20.07.2018 619

20.07.2018 578

16.06.2018 1192

14.06.2018 538

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Окружность. 7 класс.Скачать

Дистанционные курсы
для педагогов

530 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Переводить ЕГЭ по математике, физике и химии в компьютерный формат пока не планируется

Время чтения: 2 минуты

Первый мониторинг вузов РФ по новым показателям пройдёт в 2023 году

Время чтения: 2 минуты

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

В местах сдачи ЕГЭ будут применены антиковидные меры

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Зачет по геометрии окружность атанасян

Контрольная работа по геометрии в 8 классе «Окружность» с ответами и решениями (3 уровня сложности по 2 варианта). УМК Атанасян и др. (Просвещение). Поурочное планирование по геометрии для 8 класса. ГЛАВА VIII. ОКРУЖНОСТЬ. Урок 66. Геометрия 8 класс Контрольная № 5 по теме «Окружность» (Уровень 1-й, легкий).

Другие варианты контрольной № 5:

Видео:Математика это не ИсламСкачать

Контрольная работа № 5
«Окружность»

Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.

ХОД УРОКА

1. Организационный момент

Мотивация к учебной деятельности. Учитель сообщает тему урока, формулирует цели урока.

2. Выполнение контрольной работы

Контрольная работа № 5
Уровень 1 (легкий). Геометрия 8 класс

Вариант 1

1. АВ и АС — отрезки касательных, проведенные к окружности радиусом 9 см. Найдите длины отрезков АС и АО, если АВ = 12 см.
2. Дано: ∪АВ : ∪BC = 11 : 12 (рис. 8.178). Найти: ∠BCA, ∠BAC.
3. Хорды MN и РК пересекаются в точке Е так, что ME = 12 см, NE = 3 см, РЕ = КЕ. Найдите РК.
4. * Окружность с центром О и радиусом 16 см описана около треугольника АВС так, что ∠OAB = 30°, ∠OCB = 45°. Найдите стороны АВ и ВС треугольника.

Вариант 2

1. MN и МК — отрезки касательных, проведенные к окружности радиусом 5 см. Найдите MN и МК, если МО = 13 см.
2. Дано: ∪АВ : ∪АС = 5 : 3 (рис. 8.179). Найти: ∠BOC, ∠ABC.
3. Хорды АВ и CD пересекаются в точке F так, что АF = 4 см, BF = 16 см, CF = DF. Найдите CD.
4. * Окружность с центром О и радиусом 12 см описана около треугольника MNK так, что ∠MON = 120°, ∠NOK= 90°. Найдите стороны MN и NK треугольника.

3. Рефлексия учебной деятельности

В конце урока учитель раздает на каждую парту краткую запись решения задач контрольной работы.
Домашнее задание: решить задачи, с которыми ученик не справился.

Ответы на контрольную работу
I уровня сложности

Критерии оценивания результатов контрольной работы

• оценка «5» — правильно решены четыре задачи;
• оценка «4» — правильно решены три задачи или правильно решены две задачи, а при решении двух других задач допущены ошибки;
• оценка «3» — правильно решены две задачи или правильно решена одна задача, а при решении двух других задач допущены ошибки;
• оценка «2» — правильно решено менее двух задач.

За правильно решенную дополнительную задачу (№ 5) ставится дополнительная оценка.

Вы смотрели: Геометрия 8 класс Контрольная № 5. Поурочное планирование по геометрии для 8 класса. УМК Атанасян (Просвещение). Урок 66. Контрольная работа № 5 по теме «Окружность» (Уровень 1, легкий) + ОТВЕТЫ и РЕШЕНИЯ.

Другие варианты контрольной № 5:

В учебных целях использованы цитаты из учебного пособия «Поурочные разработки по геометрии. 8 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».

💡 Видео

Вся геометрия 7–9 класс с нуля | ОГЭ МАТЕМАТИКА 2023Скачать

Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Геометрия 8 класс за 1 час | Математика | УмскулСкачать

№ 144 - Геометрия 7-9 класс АтанасянСкачать

Вся геометрия за 45 минут | Геометрия 7-9 классыСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

ОКРУЖНОСТЬ задачи на построение 7 класс АтанасянСкачать

ВСЯ ГЕОМЕТРИЯ ЗА 10 МИНУТ / 7 КЛАСС / АТАНАСЯНСкачать

№ 145 - Геометрия 7-9 класс АтанасянСкачать

Задача, которую боятсяСкачать