Зачет номер 3 подобные треугольники

В данной публикации предоставляется материал к зачету по геометрии по теме «Подобные треугольники», 8 класс .

В зачет включены пять разделов: формулировки, теоремы, утверждения, задачи и задачи с практическим применением.

Так же прилагается зачетный лист с критериями оценивания.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Скачать:

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Предварительный просмотр:

Зачетный лист по геометрии учени____ 8 класса ________________________________________________________________

Критерии оценивания выполнения задания

Сформулировать устно 3 заданных утверждения

Без ошибок, верно, сформулированы утверждения

Другие случаи, не соответствующие указанным выше критериям

Доказать устно одну из теорем при следующих условиях: сделан рисунок и записано условие

Доказательство верное, все шаги обоснованы

Доказательство в целом верное, но не все шаги обоснованы

Доказательство в целом верное, но выполнено с помощью наводящих вопросов эксперта

Сформулировал без ошибок теорему, сделал соответствующий рисунок и записал условие

Другие случаи, не соответствующие указанным выше критериям

Другие случаи, не соответствующие указанным выше критериям

Указать ошибочные утверждения

Без ошибок определены все неверные утверждения, а затем они верно сформулированы

Другие случаи, не соответствующие указанным выше критериям

Решить письменно 1 задачу по изученной теме с полным обоснованием

Самостоятельно и обоснованно получен верный ответ

Решение полностью обоснованно и доведено до конца, но допущена описка или ошибка вычислительного характера, с её учётом дальнейшие шаги выполнены верно

Получен верный ответ, но обоснования неполные

Другие случаи, не соответствующие указанным критериям

Нестандартные задачи (на практическое применение)

Решить устно 1 нестандартную задачу

Самостоятельно и обоснованно получен верный ответ

Решение выполнено с помощью наводящих вопросов эксперта

Другие случаи, не соответствующие указанным критериям

Отметка «5» — 15 и более баллов

Отметка «4» — 12-14 баллов

Отметка «3» — 8-11 баллов

Зачет по теме «Подобные треугольники» 8 класс

1 блок «Формулировки»

1. Сформулируйте определение пропорциональных отрезков.
2. Сформулируйте определение подобных треугольников.
3. Сформулируйте определение сходственных сторон
   треугольника.
4. Сформулируйте определение среднего пропорционального для
   отрезков.
5. Сформулируйте свойство высоты прямоугольного
   треугольника, проведённой из вершины прямого угла
6. Сформулируйте свойство биссектрисы треугольника.

1. Сформулируйте и докажите первый признак подобия треугольников.
2. Сформулируйте и докажите теорему об отношении площадей
   подобных треугольников.
3. Сформулируйте и докажите второй признак подобия треугольников.
4. Сформулируйте и докажите третий признак подобия треугольников.
5. Сформулируйте и докажите теорему о средней линии треугольника.
6. Сформулируйте и докажите теорему о средней линии треугольника.
7. Сформулируйте и докажите теорему Пифагора

3 блок «Ошибочные утверждения»

Укажите номера ошибочных утверждений

1. Если угол одного треугольника равен углу другого треугольника, то такие треугольники подобны.
2. Если два угла одного треугольника соответственно пропорциональны двум углам другого треугольника, то такие треугольники подобны.
3. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны.
4. У двух подобных треугольников сходственные стороны пропорциональны
5. Любые два равнобедренных треугольника подобны.
6. Отношение площадей двух подобных треугольников равно коэффициенту подобия
7. Любые два прямоугольных и равнобедренных треугольника подобны.
8. Любые два равносторонних треугольника подобны.
9. Если три стороны треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
10. Любые два прямоугольных треугольника подобны.
11. Два треугольника подобны, если их углы соответственно равны и

сходственные стороны пропорциональны.

1. Два равносторонних треугольника всегда подобны.
2. Если три стороны одного треугольника соответственно пропорциональны

трем сторонам другого треугольника,

то такие треугольники подобны.

1. Стороны одного треугольника имеют длины 3, 4, 6 см, стороны другого

треугольника равны 9, 14, 18 см. Подобны ли эти треугольники?

1. Периметры подобных треугольников относятся как квадраты

1. Если два угла одного треугольника равны 60 ° и 50 ° , а два угла другого

треугольника равны 50 ° и 80 ° , то такие треугольники подобны.

1. Два прямоугольных треугольника подобны, если имеют по равному острому углу.
2. Два равнобедренных треугольника подобны, если их боковые стороны

1. Если отрезки гипотенузы, на которые она делится высотой, проведенной

из вершины прямого угла, равны 2 и 8 см, то эта высота равна 4 см.

1. Если медиана треугольника равна 9 см, то расстояние от вершины

треугольника до точки пересечения медиан равно 6 см.

4 блок «Решение задач»

1. Стороны треугольника АВС равны 4см, 8см, 7 см. Найдите стороны подобного ему треугольника FNP, если его периметр равен 57 см.
2. Две сходственные стороны подобных треугольников равны 2 см и 5 см. Площадь первого треугольника 8 см 2 . Чему равна площадь второго треугольника?
3. Биссектриса BD делит сторону АС треугольника АВС на отрезки AD и CD, равные соответственно 7 см и 10,5 см, АВ = 9 см. Чему равен периметр треугольника АВС?
4. Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках М и Н соответственно, МВ = 2 см, АМ = 14 см, МН = 4 см. Чему равна длина стороны АС?

1. Стороны треугольника АВС равны 11 см, 5 см, 9 см. Найдите стороны подобного ему треугольника КМН, если его периметр равен 100 см.
2. Площади двух подобных треугольников равны 16 см 2 и 25 см 2 . Одна из сторон первого треугольника равна 2 см. Чему равна сходственная ей сторона другого треугольника?
3. Биссектриса BD делит сторону АС треугольника АВС на отрезки AD и CD, равные соответственно 7 см и 10,5 см, АВ = 9 см. Чему равен периметр треугольника АВС?
4. Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках Е и К соответственно, ВЕ = 8 см, АВ = 12 см, ВК = 6 см, ВС = 9 см, ЕК = 10 см. Чему равна сторона АС?
5. Решите задачу. Высота CD прямоугольного треугольника о тсекает от гипотенузы AB=9 см отрезок AD=4см. Докажите,
   что треугольник ABC подобен треугольнику ACD, и найдите
   сторону AD.
6. Решите задачу. Точки M и N лежат на сторонах AC и BC треугольника ABC соответственно, причём AC=16см,
   BC=12см, CM=12см, CN=9см. Докажите, что MN || AB.
7. Площадь прямоугольника равна 36 см 2 . Найдите площадь четырёхугольника, вершинами которого
   являются середины сторон данного прямоугольника.
8. Диагонали AC и BD четырёхугольника ABCD пересекаются в точке O, AO=18см, OB=15см, OC=12см, OD=10см. Докажите, что ABCD трапеция с основаниями AB и CD.

5 блок «Задачи на практическое применение подобия»

Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?

Источник: Образовательный портал «Решу ОГЭ»

Человек ростом 1,7 м стоит на расстоянии 8 шагов от столба, на котором висит фонарь. Тень человека равна четырем шагам. На какой высоте (в метрах) расположен фонарь?

Источник: Образовательный портал «Решу ОГЭ»

Человек ростом 1,8 м стоит на расстоянии 12 м от столба, на котором висит фонарь на высоте 5,4 м. Найдите длину тени человека в метрах.

Источник: Образовательный портал «Решу ОГЭ»

Короткое плечо шлагбаума имеет длину 1 м, а длинное плечо – 3 м. На какую высоту (в метрах) опустится конец короткого плеча, когда конец длинного плеча поднимается на 1,8 м?

Источник: Образовательный портал «Решу ОГЭ»

На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?

Источник: Образовательный портал «Решу ОГЭ»

Человек, рост которого равен 1,8 м, стоит на расстоянии 16 м от уличного фонаря. При этом длина тени человека равна 9 м. Определите высоту фонаря (в метрах).

Источник: Образовательный портал «Решу ОГЭ»

Девочка прошла от дома по направлению на запад 340 м. Затем повернула на север и прошла 60 м. После этого она повернула на восток и прошла ещё 420 м. На каком расстоянии (в метрах) от дома оказалась девочка?

Источник: Образовательный портал «Решу ОГЭ»

Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 120 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 330 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?

Источник: Образовательный портал «Решу ОГЭ»

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

По теме: методические разработки, презентации и конспекты

Разработка итогового теоретического зачета по геометрии в 7 классе.

Данный материал предназначен для проведения итогового теоретического зачета по геометрии в 7 классе.Основная цель зачёта — подготовительная работа к ГИА.

Зачет по геометрии 8 класс по теме «Площади фигур. Теорема Пифагора»

В данной разработке представлены карточки в 23 вариантах для практической части зачета по геометрии в 8 классе по теме»площади фигур. Теорема Пифагора». В карточках отражены задачи на нахождение площа.

зачет по геометрии в 7 классе по теме «Параллельные прямые»

Работа содержит 6 вариантов карточек для проведения зачета по геометрии в 7 классе по тема «Параллельные прямые».

Материалы для зачета по геометрии по курсу 8 класса

Включает в себя формулировки для подготовки учащихся, билеты, список вопросов для полуголовых зачетов по планиметрии.Вероятно, будет полезен для физ-мат классов.

Вопросы к зачетам по геометрии в 7 классе УМК:Геометрия: 7класс / А.Г.Мерзляк, В.Б.Полонский , М.С.Якир

Приведены вопросы к зачетам по геометрии в 7 классе. Всего зачетов четыре, согласно основным темам по УМК:Геометрия: 7класс / А.Г.Мерзляк, В.Б.Полонский , М.С.Якир.

7 класс. Итоговый зачет по геометрии за курс 7-го класса

7 класс. Итоговый зачет по геометрии за курс 7-го класса.

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Теоретический зачет по теме «Подобие треугольников»

Данный тест разработан для проверки усвоения учащимися теоретических знаний по теме «Подобие треугольников и их применение».

Просмотр содержимого документа
«Теоретический зачет по теме «Подобие треугольников»»

Зачет по геометрии учени___ 8 класса __________________________ Тема: «Подобие треугольников».

Определить являются ли ниже приведенные утверждения верными (да -+, нет-)

Любые два прямоугольных треугольника подобны

Если два угла одного треугольника соответственно пропорциональны двум углам другого треугольника, то такие треугольники подобны.

Два треугольника называются подобными, если их углы соответственно равны

Если два треугольника подобны, то их соответствующие стороны равны

Отношение периметров двух подобных треугольников равно коэффициенту подобия

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны.

Любые два прямоугольных и равнобедренных треугольника подобны.

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны

Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, то такие треугольники подобны

Любые два равнобедренных треугольника подобны.

Высота прямоугольного треугольника равна среднему геометрическому между проекциями катетов на гипотенузу

Синус острого угла прямоугольного треугольника это отношение катетов треугольника

Косинус 45° не существует

Диагонали трапеции при пересечении образуют четыре подобных треугольника.

Необходимо ответить на вопросы и записать формулировку геометрического утверждения

Что такое средняя линия треугольника?

Сформулируйте свойство биссектрисы треугольника

Какие треугольники называются подобными?

Сформулируйте признаки подобия треугольников:

Запишите теорему об отношении площадей подобных треугольников.

Сформулируйте утверждение о пропорциональных отрезках в прямоугольном треугольнике.

Что такое косинус острого угла прямоугольного треугольника?

Записать основное тригонометрическое тождество.

Косинус 45º, синус 30º,тангенс 90º

Сформулировать теорему о точке пересечения медиан треугольника

(выполнить любое из предложенных заданий)

1). Доказать любой признак подобия треугольников

2). Доказать, что высота прямоугольного треугольника, проведенная из вершины прямого угла , есть среднее геометрическое между проекциями катетов на гипотенузу.

Диагональ BD трапеции ABCD равна большему основанию AD этой трапеции и перпендикулярна к нему. Найдите пло­щадь трапеции, если АВ=3 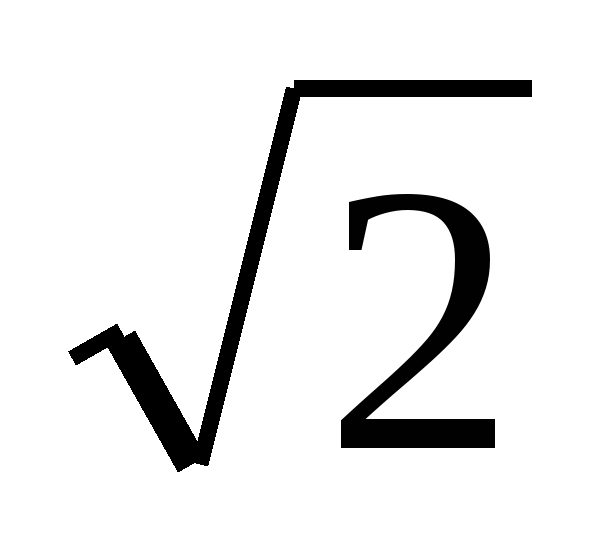см, C=60°.

Зачет по геометрии учени __ 8 класса ______________________________

Тема: «Подобие треугольников».

Определить являются ли ниже приведенные утверждения верными (да -+, нет-)

Любые два равнобедренных треугольника подобны.

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны.

Любые два равнобедренных прямоугольных треугольника подобны.

Два треугольника называются подобными, если их углы соответственно пропорциональны

Если два треугольника подобны, то их соответствующие стороны равны.

Отношение площадей двух подобных треугольников равно коэффициенту подобия

Если две стороны и угол между ними одного треугольника соответственно пропорциональны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны.

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны

Любой прямоугольный и равнобедренный треугольники подобны

Косинус это отношение противолежащего катета и гипотенузы

Тангенс прямого угла не существует

Проекция катета на гипотенузу, это отрезок гипотенузы треугольника, заключенный между основанием высоты, проведенный к гипотенузе и катетом

Диагонали трапеции при пересечении образуют два подобных треугольника.

Необходимо ответить на вопросы и записать формулировку геометрического утверждения

Сформулируйте теорему о средней линии треугольника?

Запишите определение подобных треугольников

Что называют коэффициентом подобия?

Чему равен квадрат коэффициента подобия

Сформулируйте признаки подобия треугольников:

Что такое тангенс острого угла прямоугольного треугольника

Что такое синус острого угла прямоугольного треугольника

Запишите значения синус , косинус 45º, тангенс 90º

Сформулируйте свойство биссектрисы треугольника

Теорема о высоте прямоугольного треугольника

Часть 3. (выполнить любое из данных заданий)

1). Доказать любой признак подобия треугольников

2). Доказать, что высота прямоугольного треугольника, проведенная из вершины прямого угла разбивает этот треугольник на два подобных между собой треугольника.

Диагональ BD трапеции ABCD равна меньшему основанию ВС этой трапеции и перпендикулярна к нему. Найдите пло­щадь трапеции, если CD=2 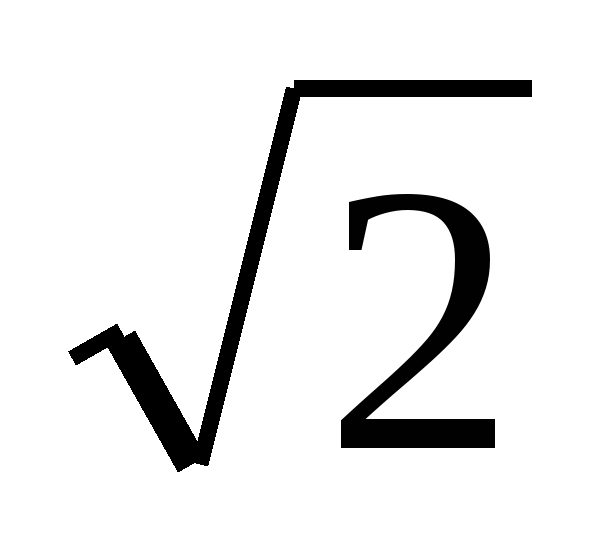см, А=30°.

Литература и интернет ресурсы.

http://imteacher.ru (теоретические зачеты)

http://www.uchportal.ru (подобие треугольников

Фарков А.В. Теоретические тесты по геометрии 8 класс. 2012 год

Кукарцева Г.И. Сборник задач по геометрии в рисунках и тестах 7-9 класс, 2000 год)

Белицкая О.В. Геометрия 8 класс. Тесты в 2-х частях. 2012 год

Видео:Подобные треугольники с нуля до ОГЭ | Математика ОГЭ 2023 | УмскулСкачать

Зачет по математике по теме «Подобные треугольники» (8 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Зачет по теме: «Подобие треугольников», 8 класс.

Составитель: Мишина Е.Р., учитель математики МБОУ гимназии №1 г.Североморск Мурманской области

Укажите номера верных утверждений

Любые два прямоугольных треугольника подобны .

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники подобны.

Если два угла одного треугольника равны 45° и 75°, а два угла другого треугольника равны 60° и 45°, то такие треугольники подобны.

Средняя линия треугольника параллельна одной из его сторон и равна половине другой его стороны.

Сформулируйте и докажите третий признак подобия треугольников .

Длина тени дерева равна 10,2 м, а длина тени человека, рост которого 1,7 м, равна 2,5 м. Найдите высоту дерева.

Стороны одного треугольника равны 3 см, 6 см и 7 см, а стороны подобного ему треугольника равны 15 см и 35 см. Найдите длину третьей стороны.

В прямоугольном треугольнике из вершины прямого угла проведена высота h .

б). Найдите высоту, если катеты прямоугольного треугольника равна 6 и 8.

Укажите номера верных утверждений

Отношение периметров двух подобных треугольников равно коэффициенту подобия в квадрате.

Стороны одного треугольника имеют длины 4 м, 5 м и 6 м. Стороны другого треугольника равны 12 м, 8 м и 10 м. Тогда эти треугольники подобны.

Если каждую сторону треугольника уменьшить в 2,5 раза, то получится треугольник, подобный первоначальному.

Два треугольника называются подобными, если их углы и стороны соответственно равны.

Сформулируйте и докажите первый признак подобия треугольника.

Через точки М и N, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая МN, параллельная стороне АС. Найдите длину СN, если ВС = 6, МN = 4 и АС = 9.

Стороны одного треугольника равны 3 см, 7 см и 6 см, а две стороны подобного ему треугольника равны 10,5 см и 4,5 см. Найдите длину третьей стороны.

В прямоугольном треугольнике из вершины прямого угла проведена высота h . Докажите, что .

Укажите номера верных утверждений

1) Любые два прямоугольных равнобедренных треугольника подобны .

2) Два треугольника называются подобными, если их углы соответственно пропорциональны.

3) Если два треугольника подобны, то их соответствующие стороны равны.

4) Если два угла одного треугольника равны 60° и 50°, а два угла другого треугольника равны 50° и 80°, то такие треугольники подобны.

Сформулируйте и докажите второй признак подобия треугольника.

Из одной точки проведены к кругу две касательные. Длина касательной равна 156, а расстояние между точками касания равно 120. Найдите радиус круга.

Прямая, параллельная основанию треугольника, отсекает от него треугольник, площадь которого в 8 раз меньше площади оставшейся части. Периметр большего треугольника равен 27. Найдите периметр меньшего треугольника.

Диагональ АС трапеции ABCD делит ее на два подобных треугольника.

а). Докажите, что АС 2 = a b , где a и b – основания трапеции.

б). Найдите длину диагонали АС, если основания трапеции равны 4 см и 9 см.

Укажите номера верных утверждений

1) Любые два равнобедренных треугольника подобны.

2) Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

3) Если внешний угол одного треугольника соответственно равен внешнему углу другого треугольника, то такие треугольники подобны.

4) Периметры подобных многоугольников относятся как сходственные стороны.

Докажите, что четырехугольник — ромб, если его вершинами являются середины сторон прямоугольника.

Прямая, параллельная основанию треугольника, делит его на треугольник и трапецию, площади которых относятся как 4:5. Периметр образовавшегося треугольника равен 20 см. Найдите периметр данного треугольника.

Боковая сторона равнобедренного треугольника равна 25 см. Из точки на основании этого треугольника проведены прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.

На стороне ВС треугольника АВС взята точка D так, что . Докажите, что AD – биссектриса треугольника АВС.

Укажите номера верных утверждений

1) Любые два равнобедренных прямоугольных треугольника подобны.

2) Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

3) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны.

4) Площади подобных многоугольников относятся как сходственные стороны.

Докажите, что четырехугольник — ромб, если его вершинами являются середины сторон равнобедренной трапеции.

Стороны двух равносторонних треугольников равны 5 см и 25 см. Найдите отношение площадей этих треугольников.

Через точки E и F, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая EF, параллельная стороне АС. Найдите длину BС, если EF = 10, AC = 15 и FC = 9.

Стороны угла О пересечены параллельными прямыми АВ и CD .

а). Докажите, что отрезки .

б). Найдите ОС, если ОВ = 3 см, АС = 10 см, BD = 2 см.

Укажите номера верных утверждений

Два равнобедренных треугольника подобны, если угол при основании одного треугольника равен углу при основании другого.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники подобны.

Если два угла одного треугольника равны 45° и 75°, а два угла другого треугольника равны 75° и 45°, то такие треугольники подобны.

Средняя линия треугольника параллельна одной из его сторон и равна половине другой его стороны.

Сформулируйте и докажите теорему об отношении площадей подобных треугольников.

Стороны треугольника имеют длину 12 см, 15 см, 24 см. определите меньшую сторону ему подобного треугольника, если его большая сторона равна 72 см.

В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O . Площадь треугольника DOC равна 4, площадь треугольника AOD равна 9. Найдите площадь трапеции.

Биссектриса внешнего угла при вершине А треугольника АВС пересекает прямую ВС в точке D .

а). Докажите, что отрезки .

б). Найдите АС, если BD = 10 см, АВ = 4 см, DC = 8 см.

Укажите номера верных утверждений

1) Два равнобедренных треугольника подобны, если боковые стороны одного треугольника пропорциональны боковым сторонам другого треугольника.

2) Два равнобедренных треугольника подобны, если их углы при вершине равны между собой.

3) Два равных треугольника подобны.

4) Два прямоугольных треугольника подобны, если они имеют равные гипотенузы.

Сформулируйте и докажите теорему об отношении периметров подобных треугольников.

Основание треугольника больше средней линии, параллельной данному основанию, а 3 см. Чему равна сумма средней линии и основания треугольника.

Ученик 8 класса, рост которого 1 м 65 см стоит рядом с деревом. Длина тени ученика равна 62 см, а длина тени дерева 3 м 10 см. Вычислить высоту дерева.

Дан параллелограмм ABCD . Через точку D и точку L , принадлежащую стороне параллелограмма ВС, и такую, что BL : LC = 4 : 3, проведена прямая д пересечения с продолжением стороны АВ в точке К. найдите длину ВК и отношение площадей треугольников BKL и ADK , если АВ = 30 см.

Укажите номера верных утверждений

Отношение периметров двух подобных треугольников равно коэффициенту подобия .

Стороны одного треугольника имеют длины 4 м, 5 м и 4 м. Стороны другого треугольника равны 10 м, 8 м и 12 м. Тогда эти треугольники подобны.

Если каждую сторону треугольника уменьшить в 2,25 раза, то получится треугольник, подобный первоначальному.

Два треугольника называются подобными, если их углы соответственно пропорциональны и стороны равны.

Сформулируйте и докажите теорему о свойстве медиан треугольника.

Стороны треугольника относятся как 2 : 3 : 4. Меньшая сторона подобного ему второго треугольника равна 4 см. Вычислить периметр второго треугольника.

Человек ростом 1,7 м стоит на расстоянии 8 шагов от столба, на котором висит фонарь. Тень человека равна четырем шагам. На какой высоте (в метрах) расположен фонарь?

В равнобедренной трапеции ABCD диагональ АС перпендикулярна боковой стороне CD , BE AC ( E AC ), основания трапеции равны 6 см и 10 см. Найдите АЕ : ЕС.

Задача на док-во

Задача на док-во

Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. Геометрия 7 – 9, учебник для ООУ.

Л.Д.Лаппо, М.А.Лаппо. Математика ОГЭ. Сборник заданий 2016. Изд. «Экзамен», М,2016.

Ященко И.В. ОГЭ (ГИА). 3000 задач с ответами по математике. Изд. «Экзамен», М, 2015.

Г.В. Сычёва, Н.Б. Гусева, В.А. Гусев. Математика. Тема геометрия. Тестовые задания частей 1 и 2. Изд. «Астрель», М, 2014.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 963 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 676 человек из 74 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Подобные треугольникиСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 558 098 материалов в базе

Материал подходит для УМК

«Геометрия», Погорелов А.В.

§11. Подобие фигур

Другие материалы

• 03.06.2016
• 1176
• 0

• 03.06.2016
• 674
• 0

• 03.06.2016
• 755
• 2

• 03.06.2016
• 540
• 0

• 03.06.2016
• 451
• 0

• 03.06.2016
• 1090
• 5

• 03.06.2016
• 359
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 03.06.2016 4102
• DOCX 38.4 кбайт
• 45 скачиваний
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Мишина Елена Рудольфовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет и 1 месяц
• Подписчики: 2
• Всего просмотров: 12402
• Всего материалов: 10

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили ввести пост уполномоченного по правам учителей

Время чтения: 2 минуты

Петербургская учительница уволилась после чтения на уроке Введенского и Хармса

Время чтения: 3 минуты

Новые курсы: управление детским садом, коучинг, немецкий язык и другие

Время чтения: 18 минут

В Рособрнадзоре рассказали, как будет меняться ЕГЭ

Время чтения: 2 минуты

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

💥 Видео

Контрольная работа | Геометрия | 8 класс | Подобные треугольники | Подробный разборСкачать

8 класс, 20 урок, Определение подобных треугольниковСкачать

Признаки равенства треугольников. 7 класс.Скачать

Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Решение задач на тему "Подобные треугольники". 8 классСкачать

8 класс, 24 урок, Третий признак подобия треугольниковСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Контрольная работа| Подобные треугольники | 8 класс | ГеометрияСкачать

Экзамен на кафедре бубна — Уральские Пельмени — Йошкар-ОлаСкачать

Третий признак равенства треугольников | Теорема + доказательствоСкачать

Контрольная работа №3 "Подобие треугольниковСкачать

Задача, которую боятсяСкачать

SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать