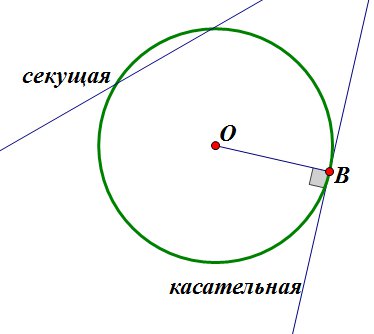
Окружности прямая имеют одну общую точку если (5 видео)

Касательная к окружности

Определение 1. Прямая, которая имеет с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

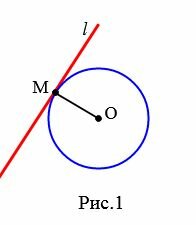
На рисунке 1 прямая l является касательной к окружности с центром O, а точка M является точкой касания прямой и окружности.

Окружности прямая имеют одну общую точку если

Содержание

Свойство касательной
Теорема, обратная теореме о свойстве касательной
Построение касательной к окружности
Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности
💡 Видео

Видео:Геометрия 8 класс (Урок№25 - Взаимное расположение прямой и окружности.)Скачать

Свойство касательной

Теорема 1 (Теорема о свойстве касательной). Касательная к окружности перпендикулярна к радиусу, проведенному из центра окружности к точке касания прямой и окружности.

Доказательство. Пусть l касательная к окружности с центром O и M − точка касания прямой и окружности (Рис.1). Докажем, что ( small l ⊥ OM .)

Предположим, что радиус OM является наклонной к прямой l. Поскольку перпендикуляр, проведенной из точки O к прямой l меньше наклонной OM, от центра окружности до прямой l меньше радиуса окружности. Тогда прямая l и окружность имеют две общие точки (см. статью Взаимное расположение прямой и окружности). Но касательная не может иметь с окружностью две общие точки. Получили противоречие. Следовательно прямая l пенрпендикулярна к радиусу OM.

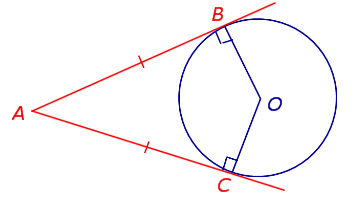
Рассмотрим две касательные к окружности с центром O, которые проходят через точку A и касаются окружности в точках B и C (Рис.2). Отрезки AB и AC называются отрезками касательных, проведенных из точки A.

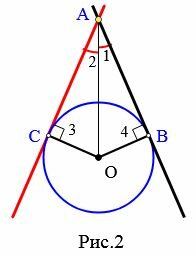Теорема 2. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через данную точку и центр окружности.

Доказательство. Рассмотрим рисунок 2. По теореме 1 касательные AC и AB перпендикулярны радиусам OC и OB, соответственно. Тогда углы 3 и 4 прямые, а треугольники ACO и ABO, прямоугольные. Эти треугольники равны по катету (OC=OB) и гипотенузе (сторона AO− общая) (подробнее см. в статье Прямоугольный треугольник. Онлайн калькулятор). Тогда AB=AC и ( small angle 1=angle 2 .) Что и требовалось доказать.

Видео:Прямая и окружность. Математика. 6 класс.Скачать

Теорема, обратная теореме о свойстве касательной

Теорема 3. Если прямая проходит через конец радиуса, лежащей на окружности и перпенжикулярна к этому радиусу, то эта прямая является касательной.

Доказательство. По условию теоремы данный радиус является перпендикуляром от центра окружности к данной прямой. То есть расстояние от центра окружности до прямой равно радиусу окружности, и, следовательно, прямая и окружность имеют только одну общую точку (теорема 2 статьи Взаимное расположение прямой и окружности). Но это означает, что данная прямая является касательной к окружности (Определение 1).

Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Построение касательной к окружности

Задача 1. Через точку M окружности с центром O провести касательную этой окружности (Рис.3).

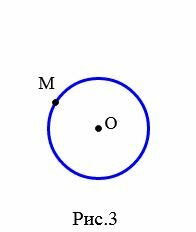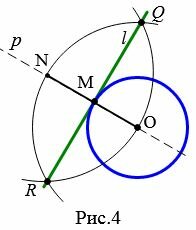Решение. Проведем прямую p через точки O и M. На прямой p из точки M отложим отрезок MN равной OM. Построим две окружности с центрами O и N и одинаковыми радиусами ON. Через точки пересечения этих окружностей проведем прямую l. Полученная прямая является касательным к окружности с центром O и радиусом OM.

Задача 2. Через точку A не принадлежащая к окружности с центром O провести касательную этой окружности (Рис.5).

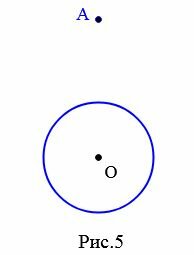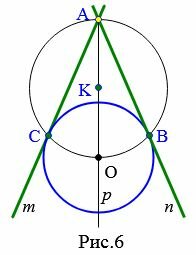Решение. Проведем прямую p через точки O и A (Рис.6). Найдем среднюю точку отрезка OA и обозначим буквой K. Постоим окружность с центром K радиусом KO=KA. Найдем точки пересечения этой окружности с окружностью с центром O. Получим точки B и C. Через точки A и C проведем прямую m. Через точки A и B проведем прямую n. Прямые m и n являются касательными к окружности с центром O.

Видео:№13. Могут ли две плоскости иметь: а) только одну общую точку; б) только две общие точкиСкачать

Взаимное расположение прямой и окружности

Существует 3 случая взаимного расположения прямой и окружности в зависимости от соотношения между радиусом r окружности и расстоянием d прямой от центра окружности.

1. d r. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.

Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Прямая, имеющая с окружностью две общие точки, называется секущей.

Теоремы о касательных и секущих

Касательная к окружности перпендикулярна радиусу, проведенному к точке касания.

Если из данной точки проведены к окружности две касательные, то отрезки касательных равны между собой и центр окружности лежит на биссектрисе угла с вершиной в этой точке: (AB=AC) .

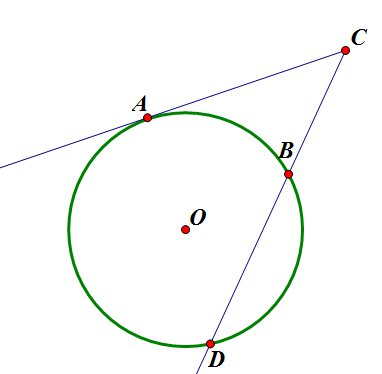
Если из данной точки проведены к окружности касательная и секущая, то квадрат длины отрезка касательной равен произведению всего отрезка секущей на его внешнюю часть: (AC^2=CDcdot BC) .

Произведение всего отрезка одной секущей на его внешнюю часть равно произведению всего отрезка другой секущей на его внешнюю часть: (ACcdot BC=ECcdot DC) .

Видео:8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать

Взаимное расположение прямой и окружности

Взаимное расположение прямой и окружности Выясним, сколько общих точек могут иметь прямая и окружность в зависимости от их взаимного расположения. Ясно, что если прямая проходит через центр окружности, то она пересекает окружность в двух концах диаметра, лежащего на. этой примой.

Пусть прямая р не проходит через центр О окружности радиуса r. Проведем перпендикуляр ОН к прямой р и обозначим буквой d длину этого перпендикуляра, т. е, расстояние от центра данной окружности до прямой (рис. 1). Исследуем взаимное расположение прямой и окружности в зависимости от соотношения между d и r. Возможны три случая.

1) d ОН= r (наклонная ОМ больше перпендикуляра ОН), и, следовательно , точка М не лежит на окружности. Итак, если расстояние от центра окружности до прямой равно радиусу то прямая и окружность имеют только одну общую точку.

3) d>r В этом случае -ОН> r поэтому .для любой точки М прямой р 0МОН.> r(рис.1,а) Следовательно точка М не лежит на окружности. Итак, .если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.

Мы доказали, что прямая и окружность могут иметь одну или две общие точки и могут не иметь ни одной общей точки. Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. На рисунке 2 прямая р — касательная к окружности с центром О, А— точка касания.

Докажем теорему о свойстве касательной.

Теорема. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

Доказательство. Пусть р— касательная к окружности с центром О. А — точка касания (см. рис. 2). Докажем. что касательная р перпендикулярна к радиусу ОА.

Предположим, что это не так. Тогда радиус: ОА является наклонной к прямой р. Так как перпендикуляр, проведенный из точки О к прямой р, меньше наклонной ОА, то расстояния от центра О окружности до прямой р меньше радиуса. Следовательно, прямая р и окружность имеют две общие точки. Но это противоречит условию; прямая р — касательная. Таким образом, прямая р перпендикулярна к радиусу ОА. Теорема доказала.

Рассмотрим две касательные к окружности с центром О, проходящие через точку А и касающиеся окружности в точках В и С (рис. 3). Отрезки АВ и АС назовем отрезками касательных, проведенными из точки А. Они обладают следующим свойством, вытекающим из доказанной теоремы:

Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Для доказательства этого утверждения обратимся к рисунку 3. По теореме о свойство касательной углы 1 и 2 прямые, поэтому треугольники АВО и АСО прямоугольные. Они равны, так как имеют общую гипотенузу ОА и равные катеты ОВ и ОС. Следовательно, АВ=АС и 3=4, что и требовалось доказать. Докажем теперь теорему, обратную теореме о свойстве касательной (признак касательной).

Теорема. Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.

Доказательство. Из условия теоремы следует, что данный радиус является перпендикуляром, проведенным из центра окружности к данной прямой. Поэтому расстояние от центра окружности до прямой равно радиусу, и, следовательно, прямая и окружность имеют только одну общую точку. Но это и означает, что данная прямая является касательной к окружности, Теорема доказана.

На этой теореме основано решение задач на построение касательной.

Прямая и окружность могут, очевидно, находиться только в следующих трех относительных положениях:

1) Расстояние (ОС) центра от прямой (АВ) (т. е, длина перпендикуляра ОС, опущенного из центра на прямую) больше радиуса окружности (рис. 1). Тогда точка С прямой удалена от центра больше, чем радиус, и потому лежит вне круга. Так как все остальные точки прямой удалены от О еще более, чем точка С (наклонные длиннее перпендикуляра), то они все лежат вне круга, значит, тогда прямая не имеет никаких точек, общих с окружностью.

2) Расстояние (ОС) центра от прямой меньше радиуса. В этом случае (рис.2) точка С лежит внутри круга и тогда, очевидно, прямая пересекается с окружностью.

3> Расстояние (ОС) центра от прямой равно радиусу. Тогда точна С (рис. 3) принадлежит и прямой, и окружности, все же остальные точки прямой, будучи удалены от О более, чем точка С, лежат вне круга. Значит, в этом случае Прямая и окружность имеют только одну общую точку, именно ту, которая служит основанием перпендикуляра, опущенного из центра на прямую.

Такая прямая, которая с окружностью имеет только одну общую точку, называется касательной к окружности; общая точка называется точкой касания.

Относительно касательной мы докажем следующие две теоремы (прямую и обратную) (рис. 4):

1) если прямая (MN) перпендикулярна к радиусу (ОА) в конце его (А), лежащем на окружности, то она касается окружности, и обратно (рис. 4);

2) если прямая касается окружности, то радиус, проведенный в точку касания, перпендикулярен к ней.

1) Точка А, как конец радиуса, лежащий на окружности, принадлежит этой окружности; в то же время она принадлежит и прямой MN, Значит, эта точка есть общая у окружности и прямой. Все же остальные точки прямой MN, как В, С и другие, отстоят от центра О дальше, чем на радиус (так как отрезки ОВ, ОС, . как наклонные, больше перпендикуляра ОА), и потому они лежат вне окружности. Таким образом, у прямой MN есть только одна точка (А), общая с окружностью, и, значит, прямая MN есть касательная.

2) Если МN касается окружности в точке А, то все остальные точки этой прямой должны лежать вне окружности; вследствие этого отрезки ОВ, ОС, . больше радиуса ОА (точка О есть центр окружности). Значит, этот радиус есть наименьший из отрезков, соединяющих точку О с любой точкой прямой MN, и потому ОА | MN.

Теорема. Если касательная параллельна хорде, то точка касания делит дугу, стягиваемую хордой, пополам.

Пусть прямая АВ касается окружности в точке М (рис. 5) и параллельна хорде CD; требуется доказать, что .

Проведя через точку касания диаметр МЕ, будем иметь: ; поэтому

Зависимость между дугами, хордами и расстояниями хорд от центра.

Теоремы. В одном круге или в равных кругах:

1) если дуги, равны, то стягивающие их хорды равны и одинаково удалены от центра;

2) если две дуги, меньшие полуокружности, не равны, то большая из них стягивается большей хордой и из обеих хорд большая расположена ближе к центру.

1) Пусть дуга АВ равна дуге CD (рис. 1), требуется доказать, что хорды АВ и CD равны, а также равны и перпендикуляры ОЕ и OF, опущенные из центра на хорды.

Повернем сектор OAJB вокруг центра О в направлении, указанном стрелкой на столько, чтобы радиус ОБ совпал с ОС. Тогда дуга ВА. пойдет по дуге CD и вследствие их равенства эти дуги совместятся. Значит, хорда AS совместится с хордой CD и перпендикуляр ОЕ совпадет с OF (из одной точки можно опустить на прямую только один перпендикуляр), т. е. AB=CD и OE=OF.

2) Пусть дуга АВ (рис. 2) меньше дуги CD, и притом обе дуги меньше полуокружности; требуется доказать, что хорда АВ меньше хорды CD, а перпендикуляр ОЕ больше перпендикуляра OF. Отложим на дуге CD дугу СК, равную АВ, и проведем вспомогательную хорду СК, которая, по доказанному, равна хорде АВ и одинаково с ней удалена от центра. У треугольников COD и СОК две стороны одного равны двум сторонам другого (как радиусы), а углы, заключенные между этими сторонами, не равны; в этом случае, как мы знаем, против большего из углов, т. е. lCOD, должна лежать большая сторона, значит, CD>CK, и потому CD>AB.

Для доказательства того, что OE>OF, проведем OLXCK и примем во внимание, что, по доказанному, OE=OL; следовательно, нам достаточно сравнить OF с OL. В прямоугольном треугольнике 0FM (покрытом на рисунке штрихами) гипотенуза ОМ больше катета OF; но OL>OM; значит, и подавно OL>OF. и потому OE>OF.

Теорема, доказанная нами для одного круга, остается верной и для равных кругов, потому что такие круги один от другого отличаются только положением.

Обратные теоремы. Так как в предыдущем параграфе рассмотрены всевозможные взаимно исключающие случаи относительно сравнительной величины двух дуг одного радиуса, причем получились взаимно исключающие выводы относительно сравнительной величины хорд и расстояний их от центра, то обратные предложения должны быть верны, в. именно:

В одном круге или е равных кругах:

1) равные хорды одинакова удалены от центра и стягивают равные дуги;

2) хорды, одинаково удаленные от центра, равны и стягивают равные дуги;

3) из двух неравных хорд большая ближе к центру и стягивает большую дугу;

4) из двух хорд, неодинаково удаленных от центра, которая ближе к центру, больше и стягивает большую дугу.

Эти предложения легко доказываются от противного. Например, для доказательства первого из них рассуждаем так: если бы данные хорды стягивали неравные дуги, то, согласно прямой теореме, они были бы не равны, что противоречит условию; значит, равные хорды должны стягивать равные дуги; а если дуги равны, то, согласно прямой теореме, стягивающие их хорды одинаково удалены от центра.

Теорема. Диаметр есть наибольшая из хорд.

Если соединим с центром О концы какой-нибудь хорды, не проходящей через центр, например хорды АВ (рис. 3) то получим треугольник АОВ, в котором одна сторона есть эта хорда, а две другие — радиусы, Но в треугольнике каждая сторона менее суммы двух других сторон; следовательно, хорда АВ менее суммы двух радиусов; тогда как всякий диаметр CD равен сумме двух радиусов. Значит, диаметр больше всякой хорды, не проходящей через центр. Но так как диаметр есть тоже хорда, то можно сказать, что диаметр есть наибольшая из хорд.

Как уже было сказано, отрезки касательных, проведенных к окружности из одной точки, имеют одинаковую длину. Эту длину называют касательным расстоянием от точки до окружности.

Без теоремы о касательных не обходиться решение не одной задачи о вписанных окружностях, иными словами, об окружностях, касающихся сторон многоугольника.

Касательные расстояния в треугольнике.

Найдем длины отрезков, на которые стороны треугольника АВС разбиваются точками касания с вписанной в него окружностью (рис. 1,а), например касательное расстояние tа от точки А до окружности. Сложим стороны b и c, а затем из суммы вычтем сторону а. Учитывая равенство касательных, проведенных из одной вершины, получим 2tа. Итак,

где p=(a+b+c)/2 – полупериметр данного треугольника. Длина отрезков сторон, прилегающим к вершинам В и С, равны соответственно p-b и p-c.

Аналогично, для вневписанной окружности треугольника, касающейся (снаружи) стороны а (рис. 1,б), касательные расстояния от В и С равны соответственно p-c и p-b, а от вершины А — просто p.

Заметим, что эти формулы можно использовать и «в обратную сторону».

Пусть в угол ВАС вписана окружность, причем касательное расстояние от вершины угла до окружности равно p или p-a, где p – полупериметр треугольника АВС, а а=ВС. Тогда окружность касается прямой ВС (соответственно снаружи или внутри треугольника).

В самом деле, пусть, например, касательное расстояние равно p-a. Тогда наши окружности касаются сторон угла в тех же самых точках, что и вписанная окружность треугольника АВС, а значит, совпадает с ней. Следовательно, она касается прямой ВС.

Описанный четырехугольник. Из теоремы о равенстве касательных сразу получается (рис. 2,а), что

если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны:

Отметим, что описанный четырехугольник обязательно выпуклый. Верно и обратное:

Если четырехугольник выпуклый и суммы его противоположных сторон равны, то в него можно вписать окружность.

Докажем это для четырехугольника, отличного от параллелограмма. Пусть какие-то две противоположные стороны четырехугольника, например AB и DC, при продолжении пересекутся в точке Е (рис. 2,б). Впишем окружность в треугольник ADE. Ее касательное расстояние te до точки E выражается формулой

Но по условию суммы противоположных сторон четырехугольника равны, а значит, AD+BC=AB+CD, или AD=AB+CD-BC. Подставив это значение в выражение для te, получим

а это – полупериметр треугольника BCE. Из доказанного выше условия касания следует, что наша окружность касается BC.

Две касательные, проведённые к окружности из точки вне её, равны и образуют равные углы с прямой, соединяющей эту точку с центром, что следует из равенства прямоугольных треугольников АОВ и АОВ1