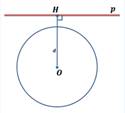
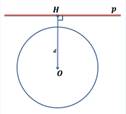
Взаимное расположение прямой и окружности тренажер (4 видео)

Тест: Взаимное расположение прямой и окружности

Взаимное расположение прямой и окружности

Сколько точек пересечения имеет окружность и секущая?

Сколько точек пересечения имеет окружность и касательная?

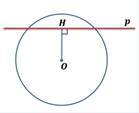
Укажите рисунок, на котором изображена секущая к окружности.

Выберите один из 3 вариантов ответа:

1) 2) 3)

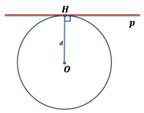
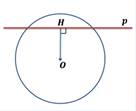
Укажите рисунок, на котором изображена касательная к окружности.

Выберите один из 3 вариантов ответа:

1) 2) 3)

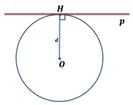
Составьте верные соответствия между соотношением расстояния от центра окружности до прямой ( d ) и радиусам окружности ( r ):

Укажите соответствие для всех 3 вариантов ответа:

1) прямая и окружность имеют две общие точки

2) прямая и окружность не имеют общих точек

3) прямая и окружность имеют одну общую точку

Определить взаимное расположение прямой и окружности, если:

Выберите один из 3 вариантов ответа:

1) прямаяи окружность не пересекаются

2) прямая является касательной к окружности

3) прямая является секущей к окружности

Определить взаимное расположение прямой и окружности, если:

Выберите один из 3 вариантов ответа:

1) прямаяи окружность не пересекаются

2) прямая является касательной к окружности

3) прямая является секущей к окружности

Определить взаимное расположение прямой и окружности, если:

Выберите один из 3 вариантов ответа:

1) прямаяи окружность не пересекаются

2) прямая является касательной к окружности

3) прямая является секущей к окружности

Определить взаимное расположение прямой и окружности, если:

d = 2015, r = 2014

Выберите один из 3 вариантов ответа:

1) прямаяи окружность не пересекаются

2) прямая является касательной к окружности

3) прямая является секущей к окружности

Определить взаимное расположение прямой и окружности, если:

d = 2014, r = 2015

Выберите один из 3 вариантов ответа:

1) прямаяи окружность не пересекаются

2) прямая является касательной к окружности

Содержание

Взаимное расположение прямой и окружности, двух окружностей. Тренажёр
Тест «Взаимное расположение прямой и окружности. Касательная» учебно-методический материал по геометрии (8 класс) на тему
Скачать:
Предварительный просмотр:
По теме: методические разработки, презентации и конспекты
💡 Видео

Видео:Урок по геометрии ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИСкачать

Взаимное расположение прямой и окружности, двух окружностей. Тренажёр

Тема: Взаимное расположение прямой и окружности, двух окружностей.

1. Даны прямая и окружность радиуса 5. Дано расстояние d от центра окружности до прямой. Определите взаимное расположение прямой и окружности при d = 10, d = 5, d = 0, d = 4.

а) окружность и прямая касаются

б) окружность и прямая пересекаются в двух точках, причём прямая не проходит через центр окружности

в) прямая проходит через центр окружности

г) прямая и окружность не имеют общих точек

Ответ: при d=10 это г, при d=5 это а, при d=0 это в, при d=4 это б.

2.Хорда АВ окружности удалена от центра окружности на . Найдите АВ, если диаметр окружности равен 12. 1)10 2)11 3) 12 4) 13.

3. Радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 2. Как расположены эти окружности?

Ответ: Окружности касаются внутренним образом.

4. О – центр окружности, А – точка вне её. АО=10, радиус окружности равен 6, а угол ВАО равен 300 . Как расположена прямая АВ относительно окружности?

Ответ: пересекает окружность в двух точках.

5. Окружности касаются внутренним образом. Радиус меньшей окружности 3 см, радиус большей окружности — 5 см. Чему равно расстояние между центрами окружностей?

а) 8 см; б) 2 см; в) 15 см; г) 3 см.

6. Каково взаимное расположение двух окружностей, если расстояние между центрами равно 10, а радиусы равны 8 и 2?

А) внешнее касание; В) внутреннее касание; С) пересекаются; D) не пересекаются.

7. Что можно сказать о взаимном расположении прямой и окружности, если диаметр окружности равен 7,2 см, а расстояние от центра окружности до прямой равно 3,25 см?

А) касаются; В) не пересекаются. С) пересекаются; D) нет правильного ответа.

8. Даны окружность с центром О и точка А. Где находится точка А, если радиус окружности равен 7 см, а длина отрезка ОА равна 4 см?

А) внутри окружности; В) на окружности. С) вне окружности; D) нет правильного ответа.

9. Радиусы двух концентрических окружностей относятся как 4:5. Найдите их диаметры, если ширина кольца, образованного этими окружностями, равна 7 см.

Ответ: 56 см и 70 см.

10. Указать количество общих точек прямой и окружности, если:

а) расстояние от прямой до центра окружности — 6 см, а радиус окружности — 7 см;

б) расстояние от прямой до центра окружности — 7 см, а радиус окружности — 6 см;

в) расстояние от прямой до центра окружности — 8 см, а радиус окружности — 8 см.

Ответ: а – 2, б – 0, в — 1.

11. Каково взаимное расположения окружностей если расстояние между центрами d и R1, R2 их радиусы:

а) d = 1дм, R1 = 0,8дм, R2 = 0,2дм; б) d = 40см, R1 = 110см, R2 = 70см;

в) d = 12см, R1 = 5см, R2 = 3см; г) d = 15дм, R1 = 10дм, R2 = 60 см.

Ответ: а – касаются внешним образом, б – касаются внутренним образом, в – вне друг друга, г – пересекаются.

12. Найти длины двух отрезков хорды, на которые разделяет ее диаметр окружности, если длина хорды — 16 см, а диаметр ей перпендикулярен.

Ответ: 8см и 8 см.

13. а) Постройте две окружности радиусами 2 см и 4 см, расстояние между центрами которых равно нулю.

б) Начертите две окружности разных радиусов (3 см и 2 см), чтобы они касались. Отметьте отрезком расстояние между их центрами. Рассмотрите возможные варианты.

в) Постройте окружность с радиусом равным 3 см и прямую расположенную на расстоянии 4 см от центра окружности.

г) Постройте окружность с радиусом равным 4 см и прямую расположенную на расстоянии 2 см от центра окружности.

14. В угол С величиной 830 вписана окружность, которая

касается сторон угла в точках А и В, точка О – центр окружности.

Найдите угол АОВ. Ответ дайте в градусах. Ответ: 970 .

15. На окружности по разные стороны от диаметра АВ

взяты точки М и N. Известно, что угол NBA =360 .

Найдите угол NMB. Ответ дайте в градусах. Ответ: 540 .

16. Точка О – центр окружности, на которой лежат точки

А, В и С. Известно, что угол АВС=750 и угол ОАВ=430 .

Найдите угол ВСО. Ответ дайте в градусах. Ответ:320 .

17. В окружности с центром в точке О отрезки АС и ВD – диаметры.

Угол АОD равен 1480 . Найдите угол АСВ. Ответ дайте в градусах.

18. На окружности с центром в точке О отмечены точки А и В так,

что угол АОВ=660 .

Найдите длину большей дуги АВ. Ответ:2940 .

19. На рисунке изображено колесо с пятью спицами. А если бы

их было 15, то какой угол был бы между спицами? Ответ: 240 .

20. Найдите угол, который образуют минутная и часовая стрелки

часов в 16:00. Ответ дайте в градусах.

21. Через точку А, лежащую вне окружности, проведены

две прямые. Одна прямая касается окружности в точке К.

Другая прямая пересекает окружность в точках В и С,

причём АВ=3, АС=12. Найдите АК. Ответ: 6.

22. Четырёхугольник ABCD описан около окружности,

АВ=7, ВС=10, CD=14. Найдите AD.

23. Хорды АС и BD окружности пересекаются в точке Р.

ВР=15, СР=6, DP=10. Найдите АР. Ответ: 25.

24. Четырёхугольник ABCD вписан в окружность. Прямые

АВ и CD пересекаются в точке К. DK=12, BK=8, BC=6.

Найдите AD. Ответ: 9.

25. Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В. Найдите АС, если диаметр окружности равен 6 , а АВ=4. Ответ: 8.

26. Окружность пересекает стороны АВ и АС треугольника АВС в точках К и Р соответственно и проходит через вершины В и С. Найдите длину отрезка КР, если АК=14, а сторона АС в 2 раза больше стороны ВС. Ответ: 7.

27. В трапеции АВСD боковая сторона АВ перпендикулярна основанию ВС. Окружность проходит через точки С и D и касается прямой АВ в точке Е. Найдите расстояние от точки Е до прямой СD, если AD=14, BC=12. Ответ 2.

Видео:8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать

Тест «Взаимное расположение прямой и окружности. Касательная»
учебно-методический материал по геометрии (8 класс) на тему

Тест «Взаимное расположение прямой и окружности. Касательная». Геометрия 8 класс (учебник И. Атанасян)

Видео:Взаимное расположение окружности и прямой. 7 класс.Скачать

Скачать:

Вложение	Размер
test_kasatelnaya.docx	16.84 КБ

Видео:Взаимное расположение прямой и окружности, математика 6 классСкачать

Предварительный просмотр:

Фамилия имя ______________________________________________

«Взаимное расположение прямой и окружности. Касательная» 1 вариант

Среди следующих утверждений укажите истинное: «Окружность и прямая имеют две общие точки, если:

расстояние от центра окружности до прямой равно радиусу окружности;
расстояние от центра окружности до прямой меньше радиуса окружности;
расстояние от центра окружности до прямой больше радиуса окружности.

Закончите фразу, чтобы получилось верное высказывание: «Окружность и прямая имеют одну общую точку, если _______________________________________________________________».

Вставьте пропущенные слова: «Окружность и прямая не имеют общих точек, если расстояние _________________________________________ до прямой _____________________________».
Среди следующих утверждений укажите истинное:

прямая а является секущей по отношению к окружности, если она имеет с окружностью общие точки;
прямая а является секущей по отношению к окружности, если она пересекает окружность в двух точках;
прямая а является секущей по отношению к окружности, если расстояние от центра окружности до данной прямой не больше радиуса.

Признак касательной: «Если прямая проходит через конец радиуса, лежащий на окружности, и ____________________________________________________ , то она является касательной».

Если АВ и АС – отрезки касательных к окружности, проведенные из одной точки А , то они _____________________________________________________________________________.

Начертите окружность с центром в точке О . Возьмите точку А на окружности и проведите касательную к окружности в этой точке.

Фамилия имя ______________________________________________

«Взаимное расположение прямой и окружности. Касательная» 2 вариант

Среди следующих утверждений укажите истинное: «Окружность и прямая не имеют общих точек, если:

расстояние от центра окружности до прямой равно радиусу окружности;
расстояние от центра окружности до прямой меньше радиуса окружности;
расстояние от центра окружности до прямой больше радиуса окружности.

Закончите фразу, чтобы получилось верное высказывание. «Окружность и прямая имеют две общие точки, если . _____________________________________________________________».

Вставьте пропущенные слова: «Окружность и прямая имеют одну общую точку, если расстояние _______________________________ до прямой _____________________________».

Среди следующих утверждений укажите истинное:

прямая а является касательной по отношению к окружности, если она имеет с окружностью общие точки;
прямая а является касательной по отношению к окружности, если она с окружностью имеет только одну общую точку;
прямая а является касательной по отношению к окружности, если она касается центра окружности.

Свойство касательной: «Касательная к окружности ________________________ радиусу, проведенному в точку касания».

Если АВ и АС – отрезки касательных к окружности, проведенных из точки А , а О – центр окружности, то углы ОВА и ОСА ______________________.

Начертите окружность с центром в точке О . Возьмите точку А на окружности и проведите секущую к окружности, проходящую через точку А .

Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

По теме: методические разработки, презентации и конспекты

Семинар-практикум по теме: «Взаимное расположение прямой и окружности».

Цель: закрепить умение определять взаимное расположение прямой и плоскости, проверить навыки решения задач, воспитывать чувство коллективизма. .

взаимное расположение прямой и окружности. 8класс.

В презентацию помещены четыре устные задачи, решаемые по готовым чертежам. Цель: подготовить учащихся к изучению нового материала.

Взаимное расположение прямой и окружности. Взаимное расположение двух ркружностей.

Конспект и презентация к уроку по теме «Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей». Урок в 6 классе по учебнику «Математика — 6» под ред. Г.В. Дорофеев, И.

Взаимное расположение прямой и окружности. Касательная к окружности.

Цели и задачи:образовательные – добиться умения самостоятельно формулировать определения понятий: окружность, радиус, диаметр, хорда каждым учащимся, изучить возможности взаимного расположения п.