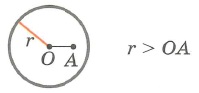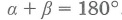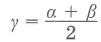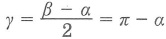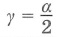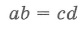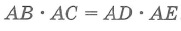Внизу приведена задача, с решением которой возникли трудности.
Как находить кол-во точек пересечения?
Варианты 3,4,7 вызвали трудности.
Даны координаты центра круга и его радиус, а также координаты центра
квадрата и его длина стороны.
Найти взаимное расположение фигур.
Набросок вариантов:
1) Окружность вписана в квадрат
2) Окружность описана вокруг квадрата
3) Окружность и квадрат касаются в одной точке (внешнее и внутреннее
касание)
4) Окружность и квадрат касаются в двух точках
5) Окружность лежит внутри квадрата
6) Квадрат лежит внутри окружности
7) Окружность и квадрат пересекаются в двух и более точках
- Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности
- Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности.
- Прямые, отрезки и углы, связанные с окружностью:
- Взаимное расположение окружности и прямой:
- Взаимное расположение окружности и точки:
- Взаимное расположение двух окружностей:
- Свойства углов, связанных с окружностью:
- Метрические соотношения в окружности (длины отрезков):
- Квадрат. Онлайн калькулятор
- Свойства квадрата
- Диагональ квадрата
- Окружность, вписанная в квадрат
- Формула вычисления радиуса вписанной окружности через сторону квадрата
- Формула вычисления сторон квадрата через радиус вписанной окружности
- Окружность, описанная около квадрата
- Формула радиуса окружности описанной вокруг квадрата
- Формула стороны квадрата через радиус описанной около квадрата окружности
- Периметр квадрата
- Признаки квадрата
- 🎬 Видео
Видео:8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать

Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности
Видео:Взаимное расположение окружностей. 7 класс.Скачать

Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности.
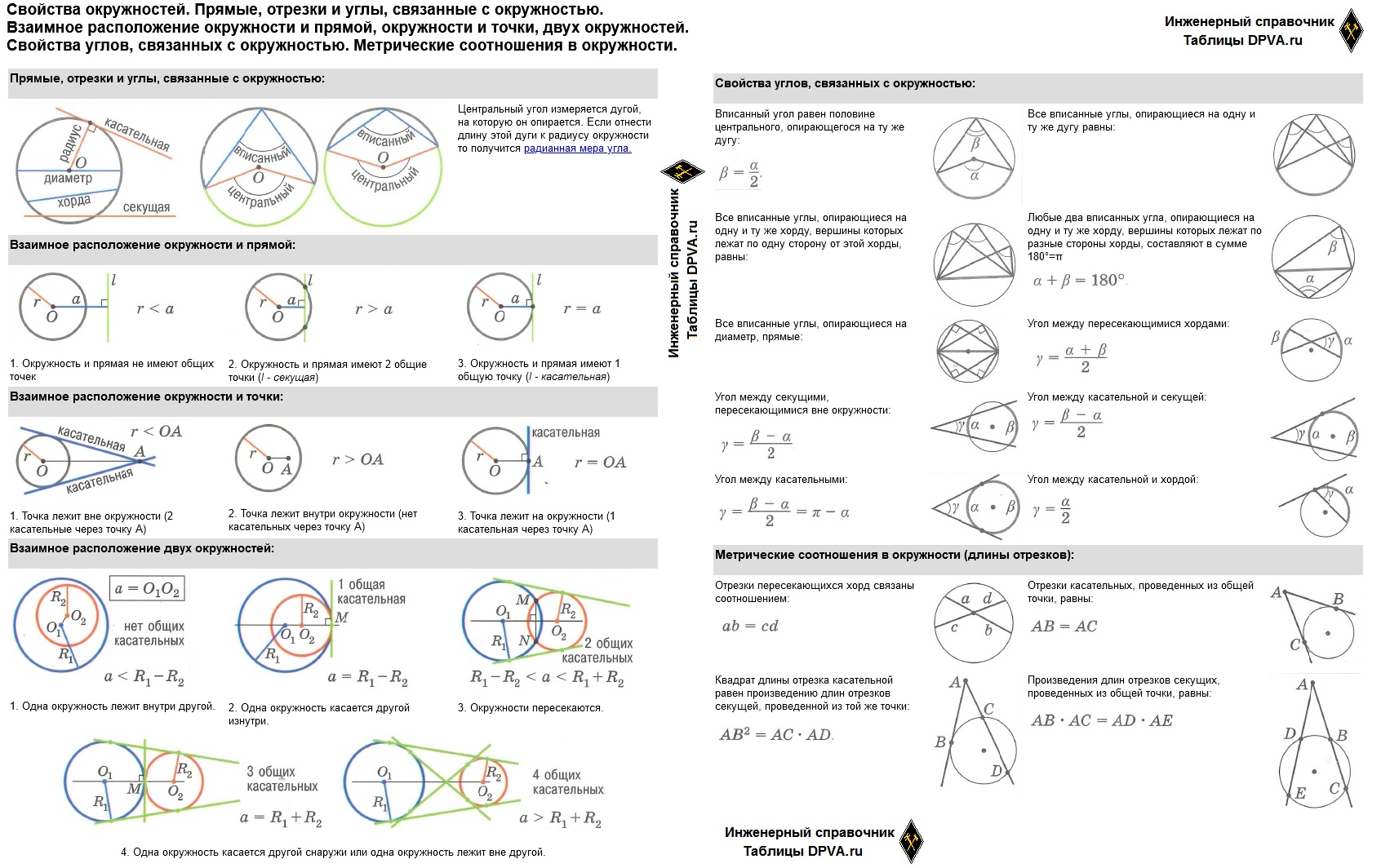
Прямые, отрезки и углы, связанные с окружностью:

Взаимное расположение окружности и прямой:
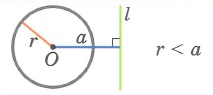
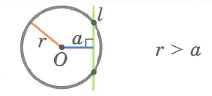
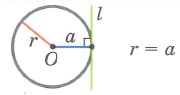
1. Окружность и прямая не имеют общих точек
2. Окружность и прямая имеют 2 общие точки (l — секущая)
3. Окружность и прямая имеют 1 общую точку (l — касательная)
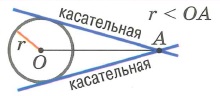
Взаимное расположение окружности и точки:
1. Точка лежит вне окружности (2 касательные через точку А)
2. Точка лежит внутри окружности (нет касательных через точку А)
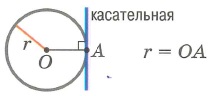
3. Точка лежит на окружности (1 касательная через точку А)
Взаимное расположение двух окружностей:
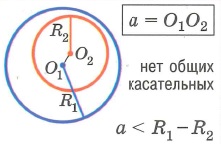
1. Одна окружность лежит внутри другой.
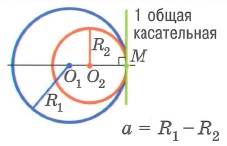
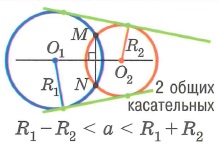
2. Одна окружность касается другой изнутри.
3. Окружности пересекаются.
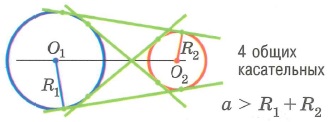
4. Одна окружность касается другой снаружи или одна окружность лежит вне другой.
Свойства углов, связанных с окружностью:
Вписанный угол равен половине центрального, опирающегося на ту же дугу:

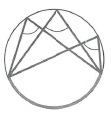
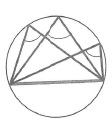
Любые два вписанных угла, опирающиеся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180°=π
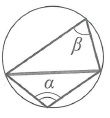
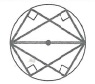
Угол между пересекающимися хордами:
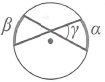
Угол между секущими, пересекающимися вне окружности:
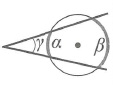
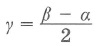
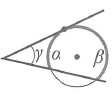
Угол между касательными:
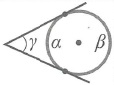
Угол между касательной и хордой:

Метрические соотношения в окружности (длины отрезков):
Отрезки пересекающихся хорд связаны соотношением:
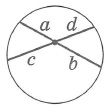
Отрезки касательных, проведенных из общей точки, равны:
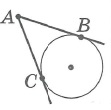
Квадрат длины отрезка касательной равен произведению длин отрезков секущей, проведенной из той же точки:
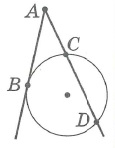
Произведения длин отрезков секущих, проведенных из общей точки, равны:
Консультации и техническая
поддержка сайта: Zavarka Team
Видео:Взаимное расположение окружности и прямой. 7 класс.Скачать

Квадрат. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):
 |
Можно дать и другие определение квадрата.
Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.
Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).
Видео:9 класс, 8 урок, Взаимное расположение двух окружностейСкачать

Свойства квадрата
- Длины всех сторон квадрата равны.
- Все углы квадрата прямые.
- Диагонали квадрата равны.
- Диагонали пересекаются под прямым углом.
- Диагонали квадрата являются биссектрисами углов.
- Диагонали квадрата точкой пересечения делятся пополам.
Изложеннные свойства изображены на рисунках ниже:
      |
Видео:Взаимное расположение окружностей. Практическая часть. 7 класс.Скачать

Диагональ квадрата
Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.
 |
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 |
 . . | (1) |
Из равенства (1) найдем d:
 . . | (2) |
Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.
Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:
 |
Ответ:
Видео:Урок по геометрии ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИСкачать

Окружность, вписанная в квадрат
Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):
 |
Видео:Взаимное расположение прямой и окружности | Геометрия 7-9 класс #68 | ИнфоурокСкачать

Формула вычисления радиуса вписанной окружности через сторону квадрата
Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:
 | (3) |
Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.
Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:
 |
Ответ:
Видео:Геометрия 8 класс (Урок№25 - Взаимное расположение прямой и окружности.)Скачать

Формула вычисления сторон квадрата через радиус вписанной окружности
Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:
 | (4) |
Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.
Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:
 |
Ответ:
Видео:Урок 47. Взаимное расположение окружностей (8 класс)Скачать

Окружность, описанная около квадрата
Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):
 |
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Формула радиуса окружности описанной вокруг квадрата
Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.
Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:
 |
 | (5) |
Из формулы (5) найдем R:
 |
 | (6) |
или, умножая числитель и знаменатель на 
 . . | (7) |
Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.
Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:
 |
Ответ:
Видео:Геометрия 9 класс (Урок№10 - Взаимное расположение двух окружностей.)Скачать

Формула стороны квадрата через радиус описанной около квадрата окружности
Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.
Из формулы (1) выразим a через R:
 |
 . . | (8) |
Пример 5. Радиус описанной вокруг квадрата окружности равен 
Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя 
 |
Ответ:
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Периметр квадрата
Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:
 | (9) |
где 
Пример 6. Сторона квадрата равен 
Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя 
 |
Ответ:
Видео:Взаимное расположение двух окружностей. Урок 8. Геометрия 9 классСкачать

Признаки квадрата
Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.
Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.
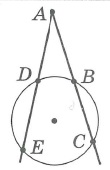
Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).
 |
Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть
 | (10) |
Так как AD и BC перпендикулярны, то
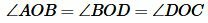 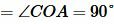 | (11) |
Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда
 | (12) |
Эти реугольники также равнобедренные. Тогда
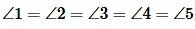 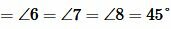 | (13) |
Из (13) следует, что
 | (14) |
Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).
🎬 Видео
Взаимное расположение прямых в пространстве. 10 класс.Скачать

ОГЭ Площадь квадрата, описанного около окружности #огэ #огэ2023 #алгебра #огэматематикаСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Взаимное расположение окружностей. Точки пересечения окружностейСкачать

70. Взаимное расположение прямой и окружностиСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Взаимное расположение двух окружностей.Использование уравнений окружности и прямой при решении задачСкачать