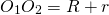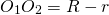Взаимное расположение двух окружностей в координатах

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

r₁ – r₂ лежит внутри другой

Длина общей хорды двух окружностей вычисляется по формуле

Видео:Геометрия 9 класс (Урок№10 - Взаимное расположение двух окружностей.)Скачать

Доказательства формул для длин общих касательных и общей хорды двух окружностей

Утверждение 1 . Если расстояние между центрами двух окружностей радиусов r₁ и r₂ равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле

что и требовалось доказать.

Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r₁ и r₂ равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле

что и требовалось доказать.

Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r₁ и r₂ равно d , то длина общей хорды AB этих окружностей вычисляется по формуле

Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3,

Видео:Взаимное расположение двух окружностей.Использование уравнений окружности и прямой при решении задачСкачать

Взаимное расположение окружностей по координатам

Видео:Взаимное расположение окружностей. Практическая часть. 7 класс.Скачать

Пересечение двух окружностей

Этот онлайн калькулятор находит точки пересечения двух окружностей, если они существуют

Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности.

Формулы для расчета приведены под калькулятором.

Точки пересечения двух окружностей

Первая окружность

Вторая окружность

Видео:Взаимное расположение двух окружностейСкачать

Пересечение окружностей

Сама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2.

При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):

Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже:

Сначала калькулятор находит отрезок a

Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде):

И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения:
Первая точка:

Обратите внимание на разные знаки перед вторым слагаемым

По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres

Видео:Взаимное расположение окружностей. 7 класс.Скачать

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2

Вступление

Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.

Начнем с взаимного расположения точки относительно прямой, луча и отрезка.

Задача №1

Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.

Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P₁(x₁, y₁), P₂(x₂, y₂). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P₁P₂ и P₁M и по его знаку сделать вывод.

Задача №2

Определить принадлежит ли точка лучу.

Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P₁(x₁, y₁) — начало луча, а P₂(x₂, y₂) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P₁(x₁, y₁), где P₂(x₂, y₂) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (P₁P₂, P₁M) ≥ 0 – скалярное произведение (точка лежит на луче)

Задача №3

Определить принадлежит ли точка отрезку.

Решение
Пусть точки P₁(x₁, y₁), P₂(x₂, y₂) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P₁, P₂. Далее нам нужно определить лежит ли точка между точками P₁ и P₂, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP₁, MP₂). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P₁(x₁, y₁), P₂(x₂, y₂) необходимо и достаточно выполнения условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (MP₁,MP₂) ≤ 0 – скалярное произведение (точка лежит между P₁ и P₂)

Задача №4

Взаимное расположение двух точек относительно прямой.

Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.

Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] 0 – точки лежат по одну сторону.
3. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] = 0 – одна (или две) из точек лежит на прямой.

Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] ≤ 0.

Задача №5

Определить пересекаются ли две прямые.

Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0. Тогда условие параллельности прямых заключается в том, что a₁b₂ — a₂b₁ = 0.
Если же прямые заданы точками P₁(x₁, y₁), P₂(x₂, y₂), M₁(x₃, y₃), M₂(x₄, y₄), то условие их параллельности заключается в проверки косого произведения векторов P₁P₂ и M₁M₂: если оно равно нулю, то прямые параллельны.

В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b₁, a₁), (-b₂, a₂) которые называются направляющими векторами.

Задача №6

Определить пересекаются ли два отрезка.

Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:

Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P₁P₂, P₁M₂] > 0, [P₁P₂, P₁M₁] [P₁P₂, P₁M₂] * [P₁P₂, P₁M₁] 2 + b 2 ).

Задача №8

Расстояние от точки до луча.

Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.

В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.

Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP₁P₂ – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
1. (P₁M, P₁P₂) 2 .

Теперь рассмотрим случай, когда центр второго круга O₂ находится между точками O₁ и C. В этом случае получим отрицательное значение величины d₂. Использование отрицательного значения d₂ приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.

Заключение

Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Урок на тему: «Взаимное расположение двух окружностей на плоскости.»

Видео:Взаимное расположение двух окружностейСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Тема урока: « Взаимное расположение двух окружностей на плоскости».

Образовательная — усвоение новых знаний о взаимном расположении двух окружностей, подготовка к контрольной работе

Развивающая — развитие вычислительных навыков, развитие логико-структурного мышления; формирование навыков нахождения рациональных путей решения и достижения конечных результатов; развитие познавательной деятельности и творческого мышления .

Воспитательная – формирование у учащихся ответственности, системности; развитие познавательных и эстетических качеств; формирование информационной культуры учащихся.

Коррекционная — развивать пространственное мышление, память, моторику рук.

Тип урока: изучение нового учебного материала, закрепление.

Вид урока: смешанный урок.

Метод обучения: словесный, наглядный, практический.

Форма обучения: коллективная.

Средства обучения: доска

1. Организационный этап

— проверка подготовленности к уроку;

2. Актуализация опорных знаний.
Какую темы мы проходили на прошлых уроках?

Общий вид уравнения окружности?

3. Введение нового материала.

Как вы думаете а какую фигуру мы сегодня будем рассматривать…. А если их две??

Как они могут быть расположены.

Дети показывают руками (соседи) как могут располагаться окружности ( физкультминутка)

Ну и как вы думаете что мы сегодня должны рассмотреть??Мы сегодня должны рассмотреть взаимное расположение двух окружностей. И выяснить каково расстояние между центрами в зависимости от расположения.

Тема урока: « Взаимное расположение двух окружностей. Решение задач. »

1. Концентрические окружности

2. Непересекающиеся окружности

4. Пересекающиеся окружности

Итак сделаем вывод

4.Формирование умений и навыков

— Найдите ошибку в данных или в утверждении и исправьте ее, обосновав свое мнение:

А) Две окружности касаются. Радиусы их равны R = 8 см и r = 2 см, расстояние между центрами d = 6.
Б) Две окружности имеют, по крайней мере, две общие точки.

В) R = 4, r = 3, d = 5. Окружности не имеют общих точек.

Г) R = 8, r = 6, d = 4. Меньшая окружность расположена внутри большей.

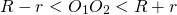
Д) Две окружности не могут располагаться так, что одна находится внутри другой.

5.Закрепление навыков и умений.

Окружности касаются внешним образом. Радиус меньшей окружности равен 3 см. радиус большей- 5 см. Чему равно расстояние между центрами?

Окружности касаются внутренним образом. Радиус меньшей окружности 3 см. Радиус большей окружности- 5 см. Чему равно расстояние между центрами окружностей?

Окружности касаются внутренним образом. Расстояние между центрами окружностей 2,5 см. Чему равны радиусы окружностей?

ответ: (5,5 см и 3 см), (6.5 см и 4 см ) и т.д.

1) Как могут располагаться две окружности?

2) В каком случае окружности имеют одну общую точку?

3) Как называется общая точка двух окружностей?

4) Какие касания вам известны?

5) Когда окружности пересекаются?

6) Какие окружности называются концентрическими?

Дополнительные задания на тему: Векторы. Метод координат »( если останется время)

1)Е(4;12), F (-4;-10), G (-2;6), H (4;-2) Найти:

а) координаты векторов EF , GH

б) длину вектора FG

в) координаты точки О – середины EF

координаты точки W – середины GH

г) уравнение окружности с диаметром FG

д) уравнение прямой FH

6. Домашнее задание

& 96 №1000. Какие из данных уравнений являются уравнениями окружности. Найти центр и радиус

7. Подведение итогов урока (3 мин.)

( дать качественную оценку работы класса и отдельных учащихся).

8. Этап рефлексии (2 мин.)

(инициировать рефлексию учащихся по поводу своего эмоционального состояния, своей деятельности, взаимодействия с учителем и одноклассниками с помощью рисунков)

Видео:УЧИМ ВМЕСТЕ (ВОЛШЕБНАЯ ГЕОМЕТРИЯ).Скачать

Дистанционные курсы для педагогов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 928 человек из 80 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 323 человека из 72 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 702 человека из 75 регионов

Ищем педагогов в команду «Инфоурок»

• Ончурова Елена ВладимировнаНаписать 3697 15.11.2017

Номер материала: ДБ-869733

15.11.2017 295

15.11.2017 244

15.11.2017 365

15.11.2017 1117

15.11.2017 205

15.11.2017 199

15.11.2017 304

15.11.2017 217

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Взаимное расположение окружностей. Точки пересечения окружностейСкачать

Дистанционные курсы
для педагогов

530 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме призвали обсуждать на школьных уроках тему опасности абортов

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В Подмосковье вводят систему голосования оценки качества школьных столовых

Время чтения: 1 минута

Стоимость обучения на первом курсе в вузах РФ за год выросла на 10%

Время чтения: 3 минуты

Федеральный перечень учебников будет дополнен новыми учебниками

Время чтения: 3 минуты

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Геометрия 16-09. Взаимное расположение двух и более окружностей. Задача 9Скачать

Взаимное расположение окружностей

Выясним, каким может быть взаимное расположение двух окружностей.

Две окружности могут пересекаться, не пересекаться либо касаться друг друга.

I. Пересекающиеся окружности имеют две общие точки.

Расстояние между центрами двух пересекающихся окружностей больше разности, но меньше суммы их радиусов:

II. Не пересекающиеся окружности не имеет общих точек.

Если одна окружность лежит внутри другой, то расстояние между центрами меньше разности их радиусов:

Если одна окружность находится вне другой, расстояние между центрами больше суммы их радиусов: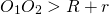

R + r]» title=»Rendered by QuickLaTeX.com»/>

III. Касающиеся окружности имеют одну общую точку — точку касания.

При внешнем касании расстояние между центрами окружностей равно сумме их радиусов:

При внутреннем касании расстояние между центрами равно разности радиусов:

Концентрические окружности разного радиуса не пересекаются. Расстояние между центрами концентрических окружностей равно нулю: O1O2=0.

🔥 Видео

Взаимное расположение окружности и прямой. 7 класс.Скачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Взаимное расположение двух окружностейСкачать

УРАВНЕНИЯ ОКРУЖНОСТИ И ПРЯМОЙ 9 класс геометрияСкачать

7 класс. Геометрия. Взаимное расположение двух окружностей. 28.04.2020.Скачать

Геометрия. 7 класс. Взаимное расположение двух окружностей /15.04.2021/Скачать

Взаимное расположение прямой и окружности Взаимное расположение двух окружностейСкачать