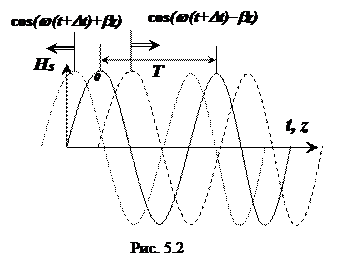Видеоурок: Опыты Герца. Свойства электромагнитных волн
Лекция: Свойства электромагнитных волн. Взаимная ориентация векторов в электромагнитной волне в вакууме
Опыты Максвелла доказали, что электрический ток в вакууме распространяется со скоростью, с которой движется свет, то есть 3*10 8 м/с.
При движении зарядов, которые создают ток, образуется две составляющих поля — электрическое и магнитное поле.

Чем быстрее будет происходить перемещение заряда, тем выразительнее будут электромагнитные волны. То есть, чем больше частота, тем большая интенсивность электромагнитных волн.
На частоту колебательного контура влияет индуктивность и ёмкость составляющих элементов цепи. Определить её можно по следующей формуле:
Электромагнитные волны являются поперечными. Это значит, что колебания магнитного и электрического поля происходят в плоскостях, которые являются параллельными к распространению волны.
На графике можно рассмотреть электрическую и магнитную составляющую электромагнитной волны.
Стоит отметить, что силовые характеристики магнитного и электрического поля находятся под углом 90 градусов друг к другу.
На графике показана длина волны, которая обозначается λ. Для её определения необходимо воспользоваться формулой:

Электромагнитным волнам присущи все правила, справедливые для механических волн:
1. Стоит отметить, что электромагнитная волна способна отразиться от плотного металла.
2. Через диэлектрик электромагнитная волна проходит достаточно проблематично, поскольку она им поглощается.
3. Если электромагнитная волна переходит из одной среды в другую, которая отличается плотностью, то она способна преломиться.
- Ориентация векторов электромагнитного поля
- 3.5.5 Свойства электромагнитных волн. Взаимная ориентация векторов в электромагнитной волне в вакууме
- Поляризация электромагнитной волны
- Поток энергии в электромагнитной волне
- Тема 5. волновые уравнения для векторов ЭМП
- Электромагнитные волны
- теория по физике 🧲 колебания и волны
- Как появляются и распространяются электромагнитные волны
- Условия возникновения электромагнитных волн
- Плотность потока электромагнитного излучения
- Точечный источник излучения
- Зависимость плотности потока излучения от частоты
- Свойства электромагнитных волн
- Шкала электромагнитных волн
- 💡 Видео
Видео:Физика 11 класс (Урок№10 - Электромагнитные волны.)Скачать

Ориентация векторов электромагнитного поля
Видео:Урок №45. Электромагнитные волны. Радиоволны.Скачать

3.5.5 Свойства электромагнитных волн. Взаимная ориентация векторов в электромагнитной волне в вакууме
Видеоурок: Опыты Герца. Свойства электромагнитных волн
Лекция: Свойства электромагнитных волн. Взаимная ориентация векторов в электромагнитной волне в вакууме
Опыты Максвелла доказали, что электрический ток в вакууме распространяется со скоростью, с которой движется свет, то есть 3*10 8 м/с.
При движении зарядов, которые создают ток, образуется две составляющих поля — электрическое и магнитное поле.

Чем быстрее будет происходить перемещение заряда, тем выразительнее будут электромагнитные волны. То есть, чем больше частота, тем большая интенсивность электромагнитных волн.
На частоту колебательного контура влияет индуктивность и ёмкость составляющих элементов цепи. Определить её можно по следующей формуле:
Электромагнитные волны являются поперечными. Это значит, что колебания магнитного и электрического поля происходят в плоскостях, которые являются параллельными к распространению волны.
На графике можно рассмотреть электрическую и магнитную составляющую электромагнитной волны.
Стоит отметить, что силовые характеристики магнитного и электрического поля находятся под углом 90 градусов друг к другу.
На графике показана длина волны, которая обозначается λ. Для её определения необходимо воспользоваться формулой:

Электромагнитным волнам присущи все правила, справедливые для механических волн:
1. Стоит отметить, что электромагнитная волна способна отразиться от плотного металла.
2. Через диэлектрик электромагнитная волна проходит достаточно проблематично, поскольку она им поглощается.
3. Если электромагнитная волна переходит из одной среды в другую, которая отличается плотностью, то она способна преломиться.
Видео:Электромагнитные волны. Шкала электромагнитных волн. 9 класс.Скачать

Поляризация электромагнитной волны
Для получения картины расположения векторов поля электромагнитной волны в пространстве необходимо ответить на последний вопрос, как ориентированы векторы , в плоскости, ортогональной направлению распространения волны ? Эта ориентация векторов создается прибором-приготовителем электромагнитной волны, или стоящим на пути ее распространения прибором-поляризатором.
Рассмотрим напряженность электрического поля , создаваемую электромагнитной волной
где — полю комплексных чисел.
Обозначим переменную фазу волны, как
Тогда из (1.2) следует, что
На самом деле, выражение (1.13) и является общим решением волнового уравнения (1.14) (запись с помощью экспоненты (1.6) просто более компактна и удобна).
Выделим в компонентном числе амплитудный множитель, согласно формуле
В (1.14) введен вспомогательный вектор , имеющий вещественный квадрат
Квадрат же вектора является комплексной величиной.
Ясно, что приведенная цепочка равенств справедлива для комплексного числа с произвольной фазой.
Проделаем описанную выше процедуру явно, положив
И потребуем его действительности
и ввиду (1.15) необходимо потребовать
что и является конкретным выбором фазы . Смысл этих конкретных действий состоит в том, что вектор принадлежит плоскости, ортогональной , . То есть, может быть разложен по ортогональному базису в этой плоскости, а и суть компоненты разложения. Ведем базис для поля явно. Пусть
Последнее выражение есть сумма двух ортогональных компонент, сдвинутых по фазе на , так как в плоскости, ортогональной . Очевидно, что константы , характеризуют волну в любой момент времени при ее распространении в пространстве.
Выберем для описания следующую систему координат
и для напряженностей электромагнитного поля , справедливо уравнение эллипса
Рис. 2 Электрическое поле электромагнитной волны в плоскости, ортогональной направлению ее расположения
Если зафиксировать конкретную точку пространства , поле в ней со временем меняется периодически согласно (1.12). То есть электромагнитная волна может быть исследована локально в этой точке. Можно поступить и иначе — провести мысленный эксперимент, сделав мгновенную фотографию пространства. Тогда профиль волны будет периодической функцией координат. Таким образом, получается представление об электромагнитной волне, как о поле. Эти периодические в пространстве и времени поля еще раскладываются на две взаимно перпендикулярные компоненты , .
Изображенная на рис. 1.2 картина имеет место в любой момент времени t в некоторой точке P пространства. При любом измерении поля волны конец вектора принадлежит эллипсу (1.2), а его полуоси суть константы , из общего решения волнового уравнения для монохроматической волны. Две независимые компоненты вектора , называются поляризациями плоской волны. Электромагнитные волны могут быть различным образом поляризованы:
Если в результате измерения оказывается, что =, то такая волна называется поляризованной по кругу.
Если реализуется частное решение =0, то волна называется линейно поляризованной.
Волна, поляризованная по кругу, может быть представлена в виде суперпозиции двух линейно поляризованных волн. Локальные измерения в 2 последовательные моменты времени t могут показать следующие изменения ориентации вектора .
Рис. 3 Возможные ориентации векторов электромагнитной волны в два последовательных момента времени
Если поворот вектора к по кратчайшему направлению осуществляется по часовой стрелке — волна — правополяризована. В противном случае она — левополяризована.
Получим аналогичные соотношения для вектора . Действительно, из свойств электромагнитных волн 1)-3) (Так как , в поляризационном эллипсе для) следует представление для
Рис. 4 Взаимное расположение поляризационных эллипсов для векторов электрического и магнитного полей электромагнитной волны
Тогда в системе координат (1.1) справедливо уравнение для компонент магнитного поля
Это означает, что при любом изменении поля конец вектора принадлежит эллипсу (1.20). Взаимное положение поляризованных эллипсов для полей , показано на рис.
Видео:Свойства электромагнитных волн | Физика 11 класс #21 | ИнфоурокСкачать

Поток энергии в электромагнитной волне
Вычислим явно поток энергии в электромагнитной волне с учетом выражения для (1.11) и разложение векторов , по поляризационному базису (1.16), (1.19). Получим выражение
Видео:ЧК_МИФ______ Электромагнитные волны в вакуумеСкачать

Тема 5. волновые уравнения для векторов ЭМП
Однородные и неоднородные волновые уравнения для векторов ЭМП. Уравнения Даламбера. Решение однородных уравнений Даламбера. Сферическая волна. Волновой фронт. Волновые уравнения Гельмгольца.
Плоские волны как частные решения волновых уравнений. Плоская волна как предельный случай сферической волны. Решения волновых уравнений для гармонических полей в виде плоских и сферических волн.
Плоские ЭМВ в однородной изотропной среде. Отличие понятий «волна» и «колебание». Свойства плоской волны, структура и ориентация векторов ЭМП. Коэффициенты фазы и ослабления. Длина волны. Фазовая скорость, скорость распространения энергии, групповая скорость.
Характеристическое и волновое сопротивления. Ослабление ЭМВ, глубина проникновения ЭМП в вещество.
Указания к теме
Решением волновых уравнений являются функции координат и времени, которые описывают ЭМВ, распространяющиеся в свободном пространстве, направляющих системах и других устройствах. Необходимо получить четкое представление о таких понятиях, как фазовая поверхность (волновой фронт) и ее форма, однородная и неоднородная волна, затухающая волна.
Следует выучить определения длины волны, коэффициентов затухания и фазы, групповой и фазовой скоростей, волнового и характеристического сопротивлений, глубины проникновения ЭМВ в вещество.
Основные сведения
Для анализа распространяющихся ЭМВ из системы уравнений Максвелла в дифференциальной форме целесообразно вывести уравнения, которые зависят либо только от 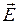
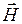
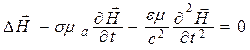
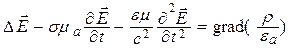
Как показали расчеты и эксперименты, константа с ( 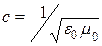
Уравнения (5.1) и (5.2) называют волновыми уравнениями Ж. Д’Аламбера [5, 12]. Если правая часть равна нулю, то уравнение называют однородным, а если нет – неоднородным. При отсутствии электрических зарядов (r = 0) уравнения (5.1) и (5.2) практически совпадают, что подтверждает равноправие векторов 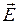
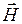
Несмотря на кажущуюся независимость уравнений (5.1) и (5.2), следует помнить о том, что у переменного ЭМП векторы 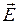
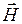
Волновые уравнения в комплексной форме имеют вид
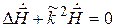
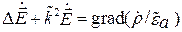
где 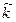
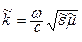
Уравнения (5.3) называют волновыми уравнениями Г. Гельмгольца. При отсутствии потерь проводимости (s = 0) исчезают вторые слагаемые в уравнениях (5.1) и (5.2), а также в (5.3)–(5.4) возможно упрощение:
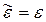
Рассмотренные уравнения называются волновыми потому, что их решениями являются волны и, в частности, ЭМВ.
Фазовым фронтом волны называют поверхность, проходящую через точки с одинаковыми фазами, по форме этой поверхности определяется название волны (сфера – сферическая ЭМВ, плоскость – плоская и т. д.) [1–3].
Решение однородного волнового уравнения для плоских волн
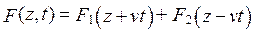
Каждое из слагаемых выражения (5.5) описывает возмущения F1 и F2, исходящие из точки z0 в момент t = 0 и к моменту времени t приходящие в точку z = z0 – vt для F1 и в точку z = z0 + vt для F2 со скоростью v [1].
Для сферических волн решение волнового уравнения имеет вид:
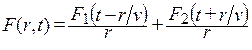
Первое слагаемое выражения (5.6) представляет собой сферическую волну, расходящуюся от источника. Второе слагаемое часто отбрасывают, поскольку волна, движущаяся внутрь источника, обычно не рассматривается [1].
В отличие от выражения (5.5) амплитуда сферической волны (5.6) уменьшается при удалении от источника как 1/r (мощность – как 1/r 2 ), что связано с тем, что мощность изотропного источника распределяется по расходящимся сферам (4.10).
Таким образом, даже при отсутствии потерь в пространстве плотность потока мощности сферической волны уменьшается с расстоянием как 1/r 2 .
На большом расстоянии от источника ЭМВ (в дальней зоне антенны) сферический волновой фронт в области приемной антенны можно аппроксимировать плоскостью, подобно тому, как земную поверхность считают плоской при малых высотах и на дистанциях, много меньших расстояния прямой видимости.
Плоская ЭМВ – идеализированная волна, имеющая плоский фазовый фронт (z = const), у которой существуют две взаимно перпендикулярные составляющие 
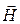
В дальнейшем будем считать, что направление распространения ЭМВ совпадает с осью z. Уравнения Максвелла в комплексной форме для составляющих векторов плоской волны в ДСК имеют вид
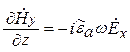
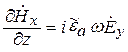
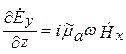
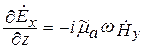
Из формул (5.7) следует, что 
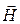
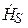
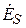
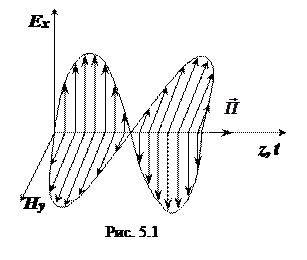
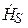
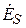
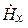
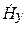
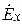
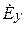
Вектор Пойнтинга в данном случае имеет только продольную составляющую 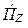
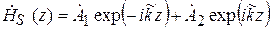
Первое слагаемое выражения (5.8) соответствует прямой волне, второе слагаемое – обратная волна, 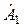
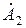

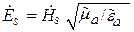
Запишем связь волнового числа ( 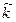
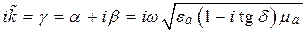
Уравнение плоской волны с учетом (5.10) можно записать в виде
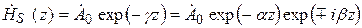
Для мгновенных значений из выражения (5.11) получаем
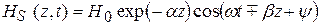
Направление распространения ЭМВ можно определить из анализа зависимости полной фазы (5.12) 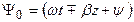
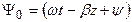
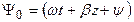
Из анализа формул (5.10)–(5.12) очевидно, что a– это коэффициент затухания, а b – коэффициент фазы.
Подставляя формулу (5.12) в (5.1), после решения уравнений относительно a и b получаем
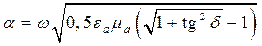
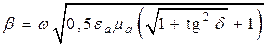
Множитель 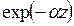
Ослаблением (A) ЭМВ по полю называют величину (AP = A 2 – ослабление ЭМВ по мощности)
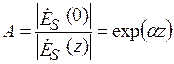
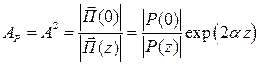
На практике часто используют ослабление в децибелах (дБ):
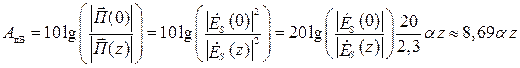
С ослаблением непосредственно связана глубина проникновения ЭМП в вещество (D° ), называемая также толщиной поверхностного слоя (скин-слоя, но это понятие логичнее использовать для металлов):
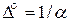
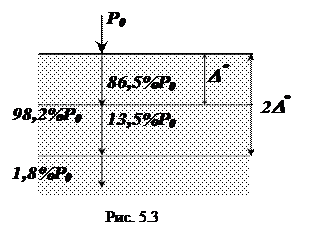
Таким образом, зная коэффициент затухания, можно определить область преимущественной концентрации энергии ЭМВ в веществе.
В случае диэлектриков толщина поверхностного слоя значительна, в то время как для проводников на ВЧ и ОВЧ она составляет доли миллиметра [1].
Параметры ЭМВ. Длиной волны l называется расстояние между двумя фронтами ЭМВ, различающимися по фазе на 2p (360°):
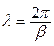
Фазовой скоростью vф называется скорость перемещения фазового (волнового) фронта ЭМВ. При анализе выражения (5.12) ранее были определены направление движения и скорость фронта ЭМВ
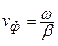
Фазовая скорость может изменяться в любых пределах (может быть больше с!), поскольку не является скоростью переноса энергии [1].
Групповой скоростью vгр называют скорость движения фронта (например, максимума) огибающеймодулированного сигнала.
Информационный сигнал не является монохроматическим, он занимает полосу частот. Каждая спектральная составляющая может иметь свою скорость распространения, что в диспергирующих средах приводит к искажениям сигнала.
Понятие «групповая скорость» вводится для сред с малыми потерями, поэтому при Dw vф ( 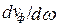
При Dw/w0 ® 0 период огибающей стремится в бесконечность, понятие «группа волн» распространяется на весь сигнал, и в итогеvгр ® vЭ.
Групповая скорость узкополосного сигнала – это скорость передачи энергии, она не может быть выше скорости света.
Характеристическое сопротивление (Zс) [41] ЭМВ равно отношению амплитуд поперечных составляющих электрического и магнитного полей
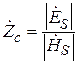

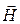

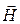

Определим характеристическое сопротивление плоской волны. Пусть 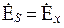
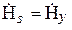
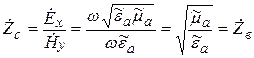
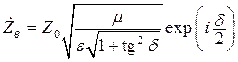
Получается, что характеристическое сопротивление [41]зависит только от параметров среды. Zв называют волновым сопротивлением среды. Следует отметить, что стандартом [41] рекомендуется термин «характеристическое сопротивление». Для ЭМВ, распространяющейся в некоторой среде, Zc = Zв.
Волновое сопротивление вакуума Z0 (s = 0, e = m = 1) :
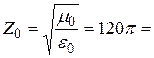
Тогда выражение (5.22) можно записать в виде
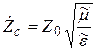
Список рекомендуемой литературы:[1, гл. 6–7, с. 30–38; 2, с. 50–56; 3, гл. 6–7, с. 27–34; 4, с. 26–33; 5, с. 26–30; 6, с. 116–123, 128–142, 198–205; 7, с. 67–82, 250–259; 8, с. 62–68; 9, с. 69–74; 10, с. 68–73; 11, с. 67–69, 130–139; 12, с. 182–194; 13, с. 140–149, 174–177, 187–190; 15, с. 302–307].
Контрольные вопросы и задания
1. Почему рассматриваемые в этой теме уравнения называются волновыми?
2. Чем волна отличается от колебания?
3. Чем отличаются волновые уравнения Д’Аламбера и Гельмгольца?
4. Следует ли из волновых уравнений независимость электрической и магнитной составляющих ЭМП?
5. Можно ли считать свет ЭМ волной?
6. Какие упрощения возможны в волновых уравнениях для сред без потерь?
7. Можно ли по виду электрической или магнитной составляющей плоской ЭМВ определить расположение другой составляющей ЭМП и направление распространения ЭМВ?
8. При каких условиях волновые уравнения для векторов 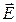
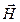
9. Каково простейшее решение системы уравнений Максвелла?
10. Дайте определение волнового фронта.
11. Почему плотность потока энергии сферической волны уменьшается при удалении от источника даже в пространстве без потерь?
12. Какие упрощения в анализе ЭМП дает понятие «плоская волна»? В каких практических случаях допустимо ЭМВ считать плоской?
13. Чем отличаются однородные и неоднородные плоские волны?
14. Дайте определение коэффициентам затухания и фазы плоской ЭМВ.
15. Чем отличается волновое число k от g ?
16. Какова пространственная структура плоской ЭМВ?
17. Как определить направление распространения ЭМВ?
18. Как с помощью понятия толщины поверхностного слоя можно оценить область преимущественной концентрации ЭМП?
19. Дайте определение основным характеристикам ЭМВ.
20. Чем групповая скорость отличается от фазовой?
21. Может ли фазовая скорость иметь бесконечное значение?
22. Чем волновое сопротивление отличается от характеристического?
23. Является ли групповая скорость скоростью передачи энергии?
24. Что такое дисперсия? Приведите примеры дисперсионных сред.
25. Укажите условие неискаженной передачи сигнала.
26. Чем нормальная дисперсия отличается от аномальной?
Видео:Что такое электромагнитная волна | Физика 11 класс #19 | ИнфоурокСкачать

Электромагнитные волны
теория по физике 🧲 колебания и волны
Вспомним, что волна — это колебания, распространяющиеся в пространстве. Механическая волна представляет собой колебания, распространяющиеся в вещественной среде. Тогда электромагнитная волна — это электромагнитные колебания, которые распространяются в электромагнитном поле.
Видео:Физика 9 класс (Урок№24 - Электромагнитные колебания. Электромагнитные волны.)Скачать

Как появляются и распространяются электромагнитные волны
Представьте себе неподвижный точечный заряд. Пусть его окружают еще много таких зарядов. Тогда он будет действовать на них с некоторой кулоновской силой (и они на него). А теперь представьте, что заряд сместился. Это приведет к изменению расстояния по отношению к другим зарядам, а, следовательно, и к изменению сил, действующих на них. В результате они тоже сместятся, но с некоторым запаздыванием. При этом начнут смещаться и другие заряды, которые взаимодействовали с ними. Так распространяется электромагнитные взаимодействия.
Теперь представьте, что заряд не просто сместился, а он начал быстро колебаться вдоль одной прямой. Тогда по характеру движения он будет напоминать шарик, подвешенный к пружине. Разница будет только в том, что колебания заряженных частиц происходят с очень высокой частотой.
Вокруг колеблющегося заряда начнет периодически изменяться электрическое поле. Очевидно, что период изменений этого поля, будет равен периоду колебаний заряда. Периодически меняющееся электрическое поле будет порождать периодически меняющееся магнитное поле. Это магнитное поле, в свою очередь, будет создавать переменное электрическое поле, но уже на большем расстояние от заряда, и т.д. В результате появления взаимно порождаемых полей в пространстве, окружающем заряд, возникает система взаимно перпендикулярных, периодически меняющихся электрических и магнитных полей. Так образуется электромагнитная волна, которая распространяется от колеблющегося заряда во все стороны.
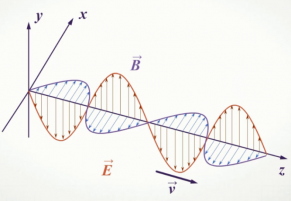
Электромагнитная волна не похожа на те возмущения вещественной среды, которые вызывают механические волны. Посмотрите на рисунок. На нем изображены векторы напряженности → E и магнитной индукции → B в различных точках пространства, лежащих на оси Oz, в фиксированный момент времени. Никаких гребней и впадин среды при этом не появляется.
В каждой точке пространства электрические и магнитные пол меняются во времени периодически. Чем дальше расположена точка от заряда, тем позднее ее достигнут колебания полей. Следовательно, на разных расстояниях от заряда колебания происходят с различными фазами. Колебания векторов → E и → B в любой точке совпадают по фазе.
Длина электромагнитной волны — расстояние между двумя ближайшими точками, в которых колебания происходят в одинаковых фазах.
Длина электромагнитной волны обозначается как λ. Единица измерения — м (метр).
Обратите внимание на рисунок выше. Векторы магнитной индукции и напряженности поля, являющиеся периодически изменяющимися величинами, в любой момент времени перпендикулярны направлению распространения волны. Следовательно, электромагнитная волна — поперечная волна.
Видео:Электромагнитная волна. Физика 11 классСкачать

Условия возникновения электромагнитных волн
Электромагнитные волны излучаются только колеблющимися заряженными частицами. При этом важно, чтобы скорость их движения постоянно менялась, т.е. чтобы они двигались с ускорением.
Наличие ускорения — главное условие возникновения электромагнитных волн.
Электромагнитное поле может излучаться не только колеблющимся зарядом, но и заряженной частицей, перемещающейся с постоянно меняющейся скоростью. Интенсивность электромагнитного излучения тем больше, чем больше ускорение, с которым движется заряд.
Представим заряд, движущийся с постоянной скоростью. Тогда создаваемые им электрическое и магнитное поля будут сопровождать его как шлейф. Только при ускорении заряда поля «отрываются» от частицы и начинают самостоятельное существование в форме электромагнитных волн.
Впервые существование электромагнитных волн предположил Максвелл, который посчитал, что они должны распространяться со скоростью света. Но экспериментально они были обнаружены лишь спустя 10 лет после смерти ученого. Их открыл Герц. Он же подтвердил, что скорость распространения электромагнитных волн равна скорости света: c = 300 000 км/с.
Видео:Физика | электродинамика | электромагнитные волны | 2 | вывод из уравнений Максвелла | для взрослыхСкачать

Плотность потока электромагнитного излучения
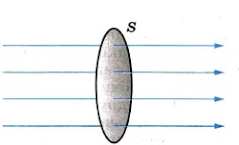
Излученные электромагнитные волны несут с собой энергию. Рассмотрим поверхность площадью S, через которую электромагнитные волны переносят энергию.
На рисунке выше прямые линии указывают направления распространения электромагнитных волн. Это лучи — линии, перпендикулярные поверхностям, во всех точках которых колебания происходят в одинаковых фазах. Такие поверхности называются волновыми поверхностями.
Плотность потока электромагнитного излучения, или интенсивность волны — отношение электромагнитной энергии ΔW, проходящей за время Δt через перпендикулярную лучам поверхность площадью S, к произведению площади S на время Δt.
Плотность потока электромагнитного излучения обозначается как I. Единица измерения — Вт/м 2 (ватт на квадратный метр). Поэтому плотность потока электромагнитного излучения фактически представляет собой мощность электромагнитного излучения, проходящего через единицу площади поверхности.
Численно плотность потока электромагнитного излучения определяется формулой:
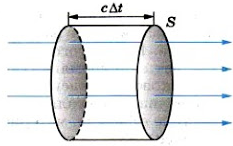
Выразим I через плотность электромагнитной энергии и скорость ее распространения с. Выберем поверхность площадью S, перпендикулярную лучам, и построим на ней как на основании цилиндр с образующей cΔt (см. рисунок ниже).
Объем цилиндра: ΔV = ScΔt. Энергия электромагнитного поля внутри цилиндра равна произведению плотности энергии на объем: ΔW = w cΔtS. Вся эта энергия за время Δt пройдет через правое основание цилиндра. Поэтому получаем:
I = w c Δ t S S Δ t . . = w c
Следовательно, плотность потока электромагнитного излучения равна произведению плотности электромагнитной энергии на скорость ее распространения.
Плотность электромагнитной энергии — энергия электромагнитного излучения в единице объема. Обозначается как w. Единица измерения — Дж/м 3 .
Пример №1. Плотность потока излучения равна 6 мВт/м 2 . Найти плотность энергии электромагнитной волны.
w = I c . . = 6 · 10 − 3 3 · 10 8 . . = 2 · 10 − 11 ( Д ж м 3 . . )
Точечный источник излучения
Источники излучения электромагнитных волн могут быть весьма разнообразными. Простейшим является точечный источник.
Точечный источник — источник излучения, размеры которого много меньше расстояния, на котором оценивается его действие.
Предполагается, что точечный источник посылает электромагнитные волны по всем направлениям с одинаковой интенсивностью. В действительности таких источников не существует. Но за такие источники излучения можно принять звезды, так как расстояние между ними существенно больше размеров самих звезд.
Энергия, которую переносят электромагнитные волны, с течением времени распределяется по все большей и большей поверхности. Поэтому энергия, передаваемая через поверхность единичной площадки за единицу времени, т. е. плотность потока излучения, уменьшается по мере удаления от источника.
Поместим точечный источник в центр сферы радиусом R. Площадь поверхности сферы S = 4πR 2 . Если считать, что источник по всем направлениям за время Δt излучает суммарную энергию ΔW, получим:
I = Δ W S Δ t . . = Δ W 4 π Δ t . . · 1 R 2 . .
Плотность потока излучения от точечного источника убывает обратно пропорционально квадрату расстояния до источника.
Пример №2. Плотность потока электромагнитного излучения на расстоянии 5 метров от точечного источника составляет 20 мВт/м 2 . Найти плотность потока электромагнитного излучения на расстоянии 10 метров от этого источника.
Расстояние по условию задачи увеличилось вдвое. Так как плотность потока излучения от точечного источника убывает обратно пропорционально квадрату расстояния до источника, при увеличении расстояния вдвое интенсивность излучения уменьшится в 4 раза. То есть, она станет равной 5 мВт/м 2 .
Зависимость плотности потока излучения от частоты
Напряженность электрического поля и магнитная индукция электромагнитной волны пропорциональны ускорению заряда. Ускорение при гармонических колебаниях пропорционально квадрату частоты. Поэтому напряженность электрического поля и магнитная индукция также пропорциональны квадрату частоты:
Плотность энергии электрического поля пропорциональна квадрату напряженности поля. Энергия магнитного поля, как это можно показать, пропорциональна квадрату магнитной индукции. Полная плотность энергии электромагнитного поля равна сумме плотностей энергий электрического и магнитного полей. Поэтому плотность потока излучения I пропорциональна:
Плотность потока излучения пропорциональна четвертой степени частоты. Так, при увеличении частоты колебаний зарядов в 2 раза энергия, излучаемая ими, возрастает в 16 раз. При увеличении частоты в 3 раза, энергия излучения увеличивается в 81 раз, и т.д.
Пример №3. Частота электромагнитной волны уменьшилась в 4 раза. Найти, во сколько раз изменилась плотность потока излучения.
Так как плотность потока излучения пропорциональна четвертой степени частоты, мы можем найти плотность потока излучения путем извлечения
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
4 √ 4 = √ √ 4 = √ 2 ≈ 1 , 4
Плотность потока излучения уменьшилась в 1,4 раза.
Видео:Урок 384. Излучение электромагнитных волн.Скачать

Свойства электромагнитных волн
Современные радиотехнические устройства позволяют провести очень наглядные опыты по наблюдению свойств электромагнитных волн. При этом лучше всего пользоваться волнами сантиметрового диапазона. Эти волны излучаются специальным генератором сверхвысокой частоты (СВЧ). Электрические колебания генератора модулируют звуковой частотой. Принятый сигнал после детектирования подается на громкоговоритель.
| Свойство 1 — Поглощение электромагнитных волн | |
 | Если расположить рупоры друг против друга и добиться хорошей слышимости звука в громкоговорители, а затем поместить между ними диэлектрик, звук будет менее громким. |
| Свойство 2 — Отражение электромагнитных волн | |
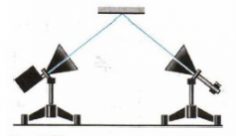 | Если диэлектрик заменить металлической пластиной, то звук перестанет быть слышимым. Волны не достигают приемника вследствие отражения. Отражение происходит под углом, равным углу падения, как и в случае световых и механических волн. Чтобы убедиться в этом, рупоры располагают под одинаковыми углами к большому металлическому листу. Звук исчезнет, если убрать Лист — наружный орган растения, основными функциями которого является фотосинтез, газообмен и транспирация. » data-gt-translate-attributes='[]’>лист или повернуть его. |
| Свойство 3 — Преломление электромагнитных волн | |
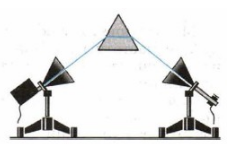 | Электромагнитные волны изменяют свое направление (преломляются) на границе диэлектрика. Это можно обнаружить с помощью большой треугольной призмы из парафина. Рупоры располагают под углом друг к другу, как и при демонстрации отражения. Металлический лист заменяют затем призмой. Убирая призму или поворачивая ее, наблюдают исчезновение звука. |
| Свойство 4 — Поперечность электромагнитных волн | |
 | Поместим между генератором и приемником решетку из параллельных металлических стержней. Решетку расположим так, чтобы стержни были горизонтальными или вертикальными. При одном из этих положений, когда электрический вектор параллелен стержням, в них возбуждаются токи, в результате чего решетка начинает отражать волны, подобно сплошной металлической пластине. Когда же вектор перпендикулярен стержням, токи в них не возбуждаются и электромагнитная волна проходит через решетку. |
Видео:Лекция №26 "Электромагнитные волны на границе раздела двух сред"Скачать

Шкала электромагнитных волн
Электромагнитные волны имеют большое разнообразие. Они классифицируются по длине волны λ или связанной с ней частоте ν. Шкала электромагнитных волн включает в себя:
- радиоволны;
- оптическое излучение;
- ионизирующее излучение.
Укажем частоты и длины указанных волн, а также их подробную классификацию в таблице.
| Наименование диапазона волн | Длины волн (м) | Частоты (Гц) |
| Радиоволны | ||
| Инфразвук, звук | >10 5 | 3 |
| Сверхдлинные волны (СДВ) | 10 4 –10 5 | 3∙10 3 –3∙10 4 |
| Длинные волны (ДВ) | 10 3 –10 4 | 3∙10 4 –3∙10 5 |
| Средние волны (СВ) | 10 2 –10 3 | 3∙10 5 –3∙10 6 |
| Короткие волны (КВ) | 10–100 | 3∙10 6 –3∙10 7 |
Ультракороткие (УКВ):
|
|
|
| Оптические волны | ||
| Инфракрасное излучение | 0,78∙10 –6 –10 –4 | 3∙10 11 –4∙10 14 |
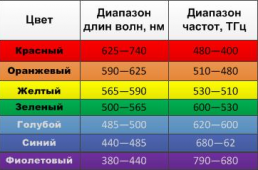
| Видимый свет | 0,38∙10 –6 –0,78∙10 –6 | 4∙10 14 –7,5∙10 14 |
| Ультрафиолетовое излучение | 10 –7 –0,38∙10 –6 | 7,5∙10 11 –3∙10 15 |
| Ионизирующее излучение | ||
| Рентгеновское излучение | 5∙10 –12 –10 –8 | 3∙10 16 –6∙10 19 |
| Гамма-излучение | –12 | >6∙10 19 |
Частоты и длины волн электромагнитного излучения видимого спектра смотрите на рисунке ниже.
В электромагнитной волне, распространяющейся со скоростью → v , происходят колебания векторов напряжённости электрического поля → E и индукции магнитного поля → B . При этих колебаниях векторы → v , → E , → B . имеют взаимную ориентацию:
💡 Видео
Энергия и импульс волны Излучение диполя Лекция 10-3Скачать

41 Шкала электромагнитных волнСкачать

Лекция №11 "Поляризация. Оптика анизотропных сред"Скачать

4.9 Поляризация электромагнитных волнСкачать

ЧК_МИФ (ЛИКБЕЗ) 3_1_1 ПЛОСКИЕ МОНОХРОМАТИЧЕСКИЕ ВОЛННЫ В ВАКУУМЕ И ИХ СВОЙСТВА (Минимум теории)Скачать

Физика | электродинамика | электромагнитные волны | 3 | вывод из уравнений Максвелла | для взрослыхСкачать

Электромагнитные волны.Скачать