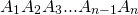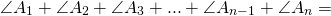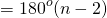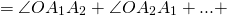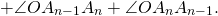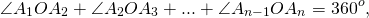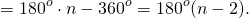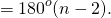Определение
Выпуклый многоугольник — это многоугольник, лежащий по одну сторону от каждой
прямой проходящей через два его соседних угла.
Правильный многоугольник — это выпуклый многоугольник,
в котором все углы и стороны равны.
Если в многоугольнике, через каждые два его соседних угла по одну сторону
проходит прямая, то многоугольник выпуклый. Многоугольник, который не
является выпуклым называется не выпуклым многоугольником.
В выпуклых многоугольниках сумма углов вычисляется по формуле: (n-2) * 180,
где n — количество сторон.
Углы многоугольника
Внутренний угол многоугольника — это угол, образованный двумя смежными сторонами многоугольника. Например, ∠ABC является внутренним углом.
Внешний угол многоугольника — это угол, образованный одной стороной многоугольника и продолжением другой стороны. Например, ∠LBC является внешним углом.
Количество углов многоугольника всегда равно количеству его сторон. Это относится и к внутренним углам и к внешним. Несмотря на то, что для каждой вершины многоугольника можно построить два равных внешних угла, из них всегда принимается во внимание только один. Следовательно, чтобы найти количество углов любого многоугольника, надо посчитать количество его сторон.
Сумма внутренних углов
Сумма внутренних углов выпуклого многоугольника равна произведению 180° и количеству сторон без двух.
где s — это сумма углов, 2d — два прямых угла (то есть 2 · 90 = 180°), а n — количество сторон.
Если мы проведём из вершины A многоугольника ABCDEF все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:
Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна 180° (2d), то сумма углов всех треугольников будет равна произведению 2d на их количество:
Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.
Сумма внешних углов
Сумма внешних углов выпуклого многоугольника равна 360° (или 4d).
где s — это сумма внешних углов, 4d — четыре прямых угла (то есть 4 · 90 = 360°).
Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна 180° (2d), так как они являются смежными углами. Например, ∠1 и ∠2:
Следовательно, если многоугольник имеет n сторон (и n вершин), то сумма внешних и внутренних углов при всех n вершинах будет равна 2dn. Чтобы из этой суммы 2dn получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть 2d(n — 2):
Сумма углов многоугольника
(о сумме углов выпуклого многоугольника)
Сумма внутренних углов выпуклого многоугольника равна 180º(n-2).
(n — количество сторон многоугольника).
Другой вариант формулировки этой теоремы:
Сумма внутренних углов выпуклого n — угольника равна 180º(n-2).
— выпуклый n -угольник.
1-й способ
Обозначим внутри многоугольника произвольную точку O.
Соединим точку O с вершинами многоугольника.
Получили n треугольников.
Сумма внутренних углов многоугольника равна сумме углов всех треугольников без углов при вершине O.
Так как сумма углов при вершине O составляет 360º
то сумма углов многоугольника равна сумме углов n треугольников минус 360º.
Таким образом, искомая сумма углов n угольника равна
Что и требовалось доказать .
2-й способ
Соединим вершину A1 со всеми остальными вершинами многоугольника. Получили n-2 треугольника.
Сумма всех углов этих треугольников равна сумме углов многоугольника.
Сумма углов углов каждого из треугольников равна 180º.
Следовательно, сумма углов многоугольника
Что и требовалось доказать.
4 Comments
Нужно либо поменять название статьи, либо добавить в текст информацию о невыпуклых многоугольниках.
А так сайт оказался полезным, спасибо!
Ольга, спасибо. Подкорректирую в июне.
Очень хороший сайт! Давно им пользуюсь. Спасибо за Ваш труд!