Докажите что диаметры этих окружностей относятся как m n

Задание:

Решение:

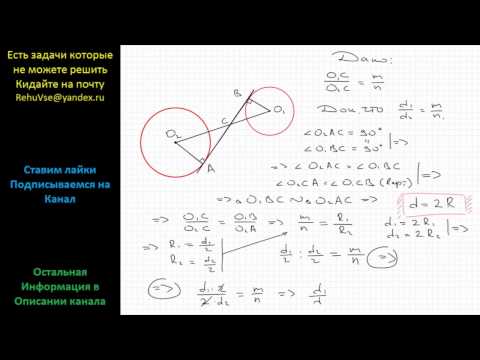
$A$ и $B$ — точки касания.

$O$ — точка пересечения касательной и отрезка, соединяющего центры окружностей $IJ$.

По условию: $IO:JO=m:n$

$IA$ и $JB$ — радиусы, проведенные в точки касания, т.е. они перпендикулярны касательной.

Углы $AOI$ и $BOJ$ равны, как вертикальные.

Треугольники $IAO$ и $JBO$ подобны по двум углам.

Значит, радиусы окружностей, соответственно и диаметры, относятся, как $m:n$.

Видео:Задача 25 ОГЭ Математика 1 ЯщенкоСкачать

Окружности с центрами в точках I и J не имеют общих точек внутренняя общая касательная к этим окружностям делит отрезок соединяющий их центры отношение M к N докажите что диаметр этих окружностей отно?

Геометрия | 5 — 9 классы

Окружности с центрами в точках I и J не имеют общих точек внутренняя общая касательная к этим окружностям делит отрезок соединяющий их центры отношение M к N докажите что диаметр этих окружностей относятся как M к N.

Даже решать нечего.

На рисунке все четко видно.

Образовались два подобныхпрямоугольных треугольника, гипотенузы которых относятся как m / n

значит и катеты, образующие радиусы, а , значит, и диаметры относятся как m / n.

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

ВС — касательная к окружности с центром О(В — точка касания)?

ВС — касательная к окружности с центром О(В — точка касания).

Найдите СО, если ВС = 8см, а диаметр окружности равен 12см.

Видео:№144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВССкачать

Отрезок АВ и СD — диаметра окружности с центром в точке О?

Отрезок АВ и СD — диаметра окружности с центром в точке О.

Докажите, что хорды АС и ВD равны.

Видео:№147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВССкачать

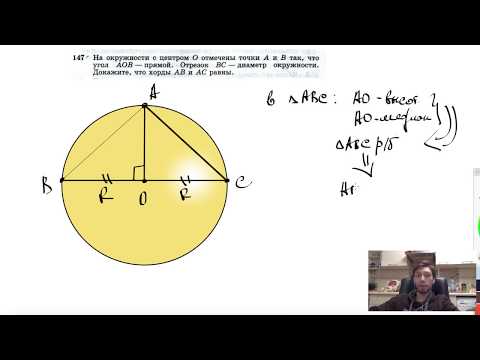
Расстояние от точки до центра данной окружности равно диаметру этой окружности?

Расстояние от точки до центра данной окружности равно диаметру этой окружности.

Найдите угол между отрезками касательных , проведенных из указанной точки к данной окружности.

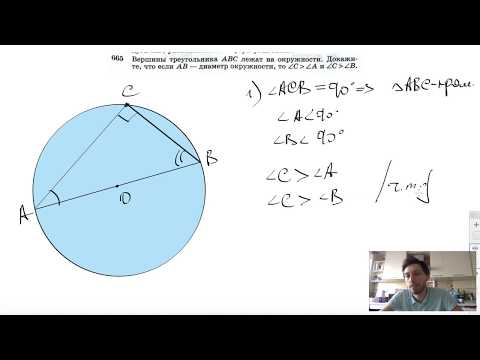
Видео:№665. Вершины треугольника ABC лежат на окружности. Докажите, что если АВ — диаметр окружностиСкачать

ПОМОГИТЕЕЕЕ)))))ПОЖАЛУЙСТА?

НУЖНО ДО ЗАВТРА.

две окружности радиуса 4 см и 6 см имеют общий центр.

Найдите расстояние между этих окружностей.

Видео:Окружность. 7 класс.Скачать

Радиусы двух окружностей 3см и 4см, а расстояние между их центрами 5см?

Радиусы двух окружностей 3см и 4см, а расстояние между их центрами 5см.

Имеют ли эти окружности общие точки.

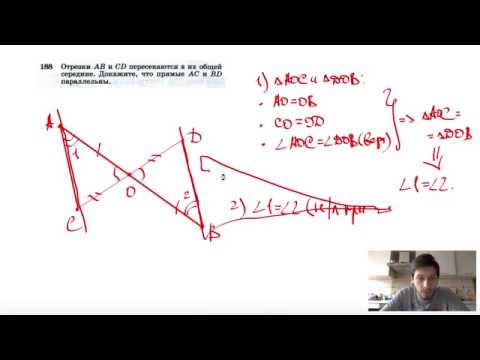
Видео:№188. Отрезки АВ и CD пересекаются в их общей середине. Докажите, что прямые АССкачать

Две окружности радиуса 4 см и 6 см имеют общий центр ( их называют концентрическими окружностями )?

Две окружности радиуса 4 см и 6 см имеют общий центр ( их называют концентрическими окружностями ).

Найдите расстояние между наиболее удаленными точками этих окружностей.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

К окружности с центром О из точки А вне окружности проведены две касательные АВ и АС?

К окружности с центром О из точки А вне окружности проведены две касательные АВ и АС.

Отрезок, соединяющий точки касания, делит отрезок АО пополам.

Найдите угол ВАС.

Видео:ОГЭ Задание 25 Условие принадлежности четырёх точек одной окружностиСкачать

Справедливы ли данные суждения?

Справедливы ли данные суждения?

1. Если прямая касательная окружности, то она имеет две общие точки с окружностью.

Если прямая и окружность имеют общую точку, то прямая является касательной окружности.

Прямая и окружность могут иметь только две общие точки.

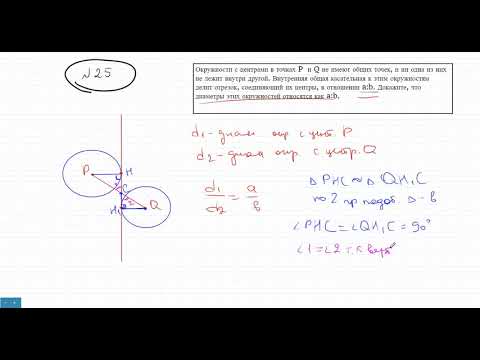
Видео:Внутренняя касательная. 25 задача ОГЭСкачать

Справедливы ли данные суждения?

Справедливы ли данные суждения?

1. Если прямая касательная окружности, то она имеет хотя бы одну общую точку с окружностью.

Если прямая и окружность имеют общую точку, то прямая является касательной окружности.

Прямая и окружность могут иметь одну или две общие точки.

Видео:Геометрия Докажите, что диаметр окружности вписанной в равнобедренную трапецию есть среднееСкачать

Из точки А к окружности проведены касательная АВ и секущая АС, проходящая через центр окружности?

Из точки А к окружности проведены касательная АВ и секущая АС, проходящая через центр окружности.

Расстояние от А до окружности равно 4см, а диаметр окружности равен 12 см.

Какова длина касательной?

Видео:ОГЭ 24 | КАК РЕШАТЬ ЗАДАЧИ НА ДОКАЗАТЕЛЬСТВО | ОКРУЖНОСТИ С ВНУТРЕННЕЙ КАСАТЕЛЬНОЙСкачать

Дана прямая l и окружность с центром в точке О и точка А на окружности, прямая l не имеет общих точек с окружностью?

Дана прямая l и окружность с центром в точке О и точка А на окружности, прямая l не имеет общих точек с окружностью.

Построить окружность, которая касается прямой l и касается окружности в точке А.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос Окружности с центрами в точках I и J не имеют общих точек внутренняя общая касательная к этим окружностям делит отрезок соединяющий их центры отношение M к N докажите что диаметр этих окружностей отно?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Видео:ОГЭ Задание 25 Две окружностиСкачать

Докажите что диаметры этих окружностей относятся как m n

Вопрос по геометрии:

Окружности с центрами в точках P и Q не имеют общих точек и не лежат одна внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в соотношении a:b. Докажите, что диаметры этих окружностей относятся как a:b.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Решение во вложенном файле.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

🔍 Видео

№710. Докажите, что если около трапеции можно описать окружность, то эта трапеция равнобедренная.Скачать

Геометрия В окружности с центром O проведены диаметр AB и хорда AC. Докажите, что угол BOC = 2 угламСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Геометрия Окружности с центрами в точках O1 и O2 не имеют общих точек. Внутренняя общая касательнаяСкачать

Все типы 24 задание 2 часть ОГЭ ПО МАТЕМАТИКЕ 2023 УмскулСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

№145. Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружностиСкачать