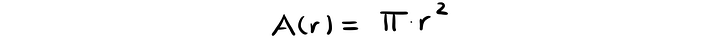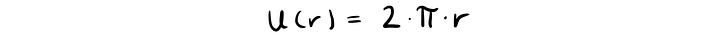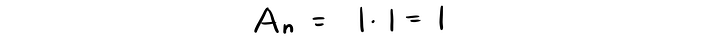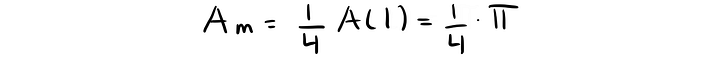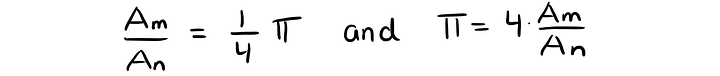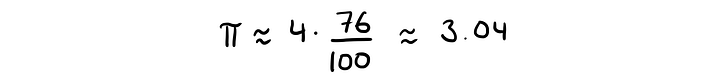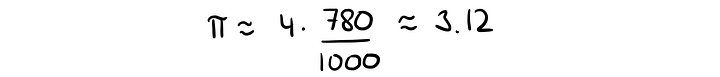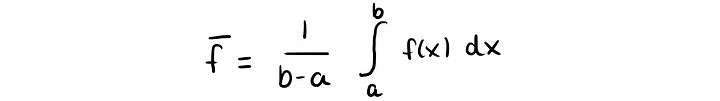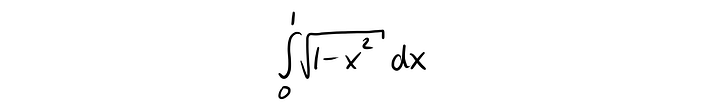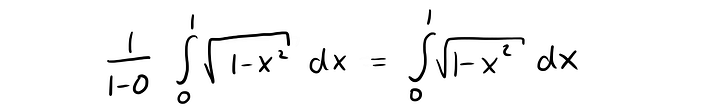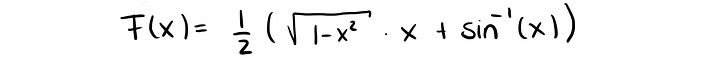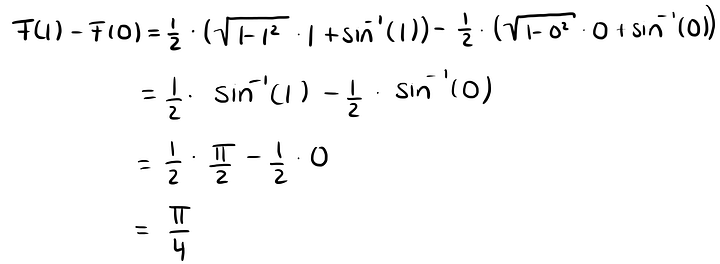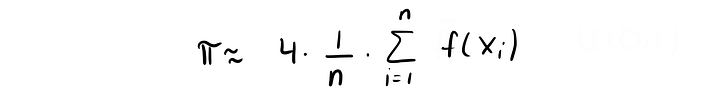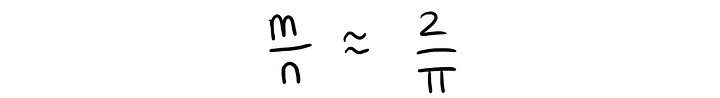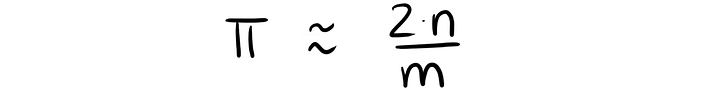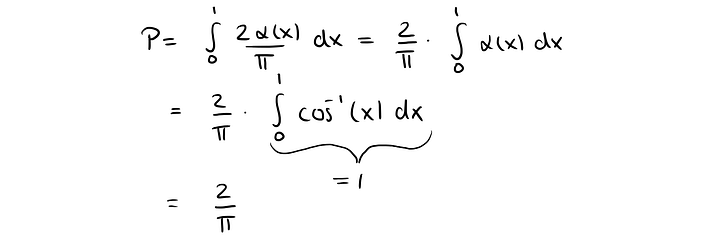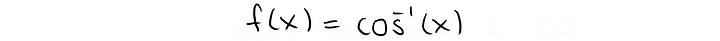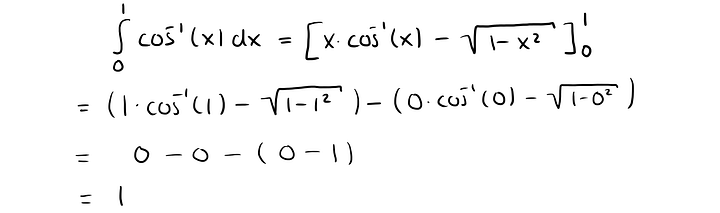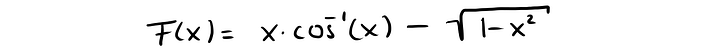Вычисляющую число пи методом интегрирования четверти окружности единичного радиуса

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Вычисление π: моделирование методом Монте-Карло

Каждый год 14 марта любители математики отмечают День числа пи! Есть много способов вычислить это легендарное число π, которое примерно равно 3,14159…

Обсудим все эти методы и рассмотрим три способа вычисления π с использованием моделирования методом Монте-Карло!

Что такое пи?

Пи — это число, которое выражает отношение длины окружности к её диаметру, приблизительно равное 3,14159…

Нарисуем единичную окружность (т.е. окружность с радиусом 1).

Как известно, площадь круга (окружности) равна:

Для единичной окружности, где r = 1, площадь равна π, а периметр равен 2π. То есть π — это есть одновременно и площадь единичной окружности, и её полупериметр.

Существует великое множество способов вычисления числа π. Помимо детерминистских методов, то есть методов без использования элемента случайности, есть ещё вероятностные методы. Последние объединяются под одним общим названием «моделирование методом Монте-Карло». Прежде чем уходить с головой в математику, разберёмся с тем, что представляет собой моделирование методом Монте-Карло.

Что такое моделирование методом Монте-Карло?

Моделирование методом Монте-Карло основано на экспериментах или вычислительных алгоритмах, использующих выборку случайных величин. Моделирование случайных величин в таких экспериментах имеет повторяющийся характер, то есть модель многократно перерасчитывается для получения данных и нахождения искомых параметров, причём последние могут быть определены и детерминированно. Например, число π является детерминированным, т.е. не зависящим от элемента случайности или вероятности.

Моделирование методом Монте-Карло применяется, когда детерминированные вычисления сопряжены со слишком большими вычислительными затратами или неосуществимы. Ну… или если экспериментатор слишком ленив для точных вычислений.

Бывает и так, что в моделировании методом Монте-Карло нет никакой необходимости, а просто хочется продемонстрировать всю красоту математики и теории вероятности.

Мне больше нравится третья причина, так что давайте скорее начнём вычислять наше любимое число π! У меня для вас три способа вычисления пи: простой, сложный и неожиданный.

Просто: единичный квадрат и единичная окружность

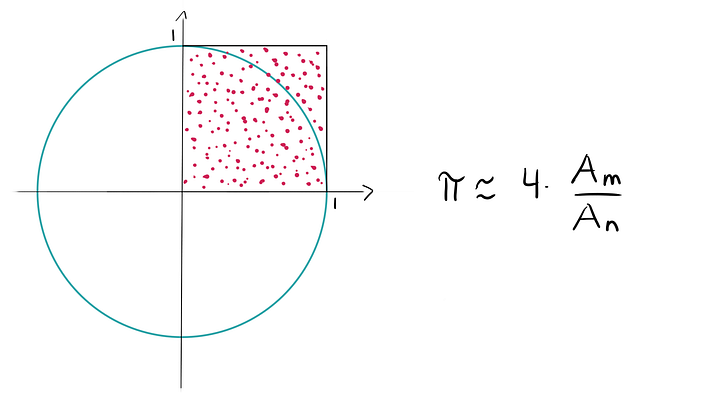
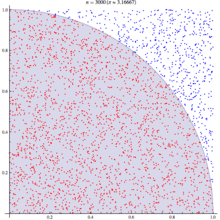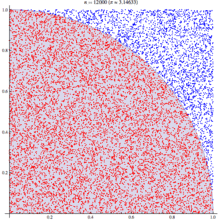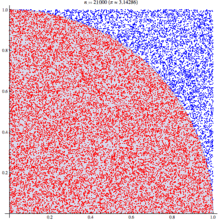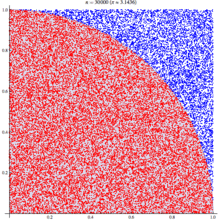
Рисуем единичный квадрат — такой же, как на рисунке ниже — и наносим, равномерно распределяя по всему квадрату, n точек. Пусть внутри круга с радиусом 1 оказалось m точек этого квадрата. Напомним, что квадрант — это четверть окружности.

Дробь m/n определяет отношение площадей квадранта и квадрата, равное 1/4 π.

Давайте разберёмся, откуда взялись такие цифры.

Площадь квадрата, в котором оказался наш квадрант с точками, определяется так:

Площадь квадранта определяется так:

Используя соотношение этих площадей, находим π:

Теперь это отношение площадей умножаем на четыре и получаем π. Например, если из 100 точек 76 оказались внутри четверти окружности, то π будет приблизительно равно:

Что ж, неплохо. Теперь нанесём 1 000 точек, 780 из которых внутри четверти окружности, тогда π будет равно:

Ещё ближе к истине! Результат будет тем точнее, чем больше точек наносится, пока мы наконец не подберёмся благодаря закону больших чисел к реальному значению π. Вот он наш самый первый и, пожалуй, самый простой — к тому же самый очевидный — метод вычисления π с использованием в расчётах элемента случайности!

Этот способ отлично подходит для общего понимания моделирования методом Монте-Карло. Его без труда могут освоить даже младшие школьники. Обратимся теперь к менее очевидному и математически более сложному способу.

2. Средние значения функций

Этот способ очень часто используют при вычислении интегралов, когда вычислительные затраты, связанные с получением точных результатов, слишком велики. Среднее значение непрерывной функции f(x) определяется следующим образом:

Мы можем использовать его для вычисления π, потому что для этой функции

равен π/4. Следовательно, и вот этот интеграл

тоже равен π/4. И среднее значение этой функции на интервале [0,1] тоже равно π/4. Вычислим это математически. Первообразная функции f(x) определяется так:

Перепроверять дважды очень муторно, вы можете поверить мне на слово. Поэтому я пропущу этот момент. Теперь мы можем вычислить неопределённый интеграл, то есть среднее приведённой выше функции:

Вычислить π мы можем, протестировав случайные значения xᵢ, i=1,…n между 0 и 1, посчитав для них f(xᵢ) и взяв среднее. Умножив на четыре, получим приблизительное значение π.

Этот способ вычисления π тоже довольно прост, хотя математическое объяснение чуть более сложное, чем для первого метода.

Его часто используют при вычислении интегралов, особенно когда точность вычисления интеграла требует больших затрат или найти первообразную не представляется возможным.

3. Неожиданный способ: бросание игл

Неожиданный и странный на первый взгляд, но очень красивый способ вычисления π: бросаем иголки. С помощью таких элегантных упрощений математика становится понятнее!

Нарисуйте на листке бумаги параллельные прямые на расстоянии примерно 4 сантиметра друг от друга. Теперь возьмите n иголок или спичек. Бросьте их на бумагу и сосчитайте количество m, оказавшихся на прямых.

Соотношение m/n будет приблизительно равно 2/π, то есть:

Отсюда выводится π:

В этом примере у нас 11 иголок, 7 из которых лежат на прямых. Здесь π вычисляется так: 2 ⋅ 11/7 ≈ 3,1428 (очень неплохо!). Не ожидали такой точности? Я и сам, признаться, не сразу понял, как мне повезло! Попробуем разобраться, почему так получилось.

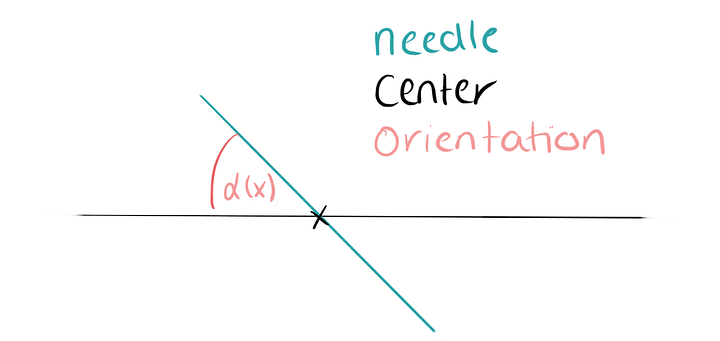
Пусть точка x находится на середине иголки. Будет иголка пересекать линию или нет, зависит только от положения иголки.

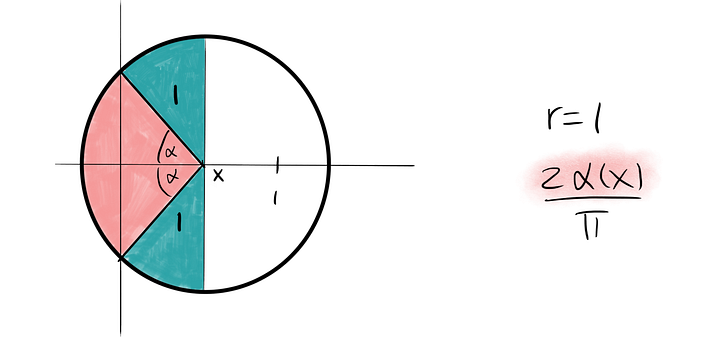
Иголка может находиться где-то между 0 и 180°, то есть π радианами. Она будет пересекать линию, если будет находиться внутри части круга, ограниченного углом 2⋅ α(x) от середины иголки.

Для радиуса r = 1 иголка длиной 1 пересечёт линию с вероятностью P, которая зависит от угла α(x). Полукруг имеет радиан π. Иголка пересекает линию, если мы в розоватом секторе. Розоватый сектор принимает дробь 2α(x)/π розового и бирюзового секторов вместе, и здесь вероятность пересечения линии будет определяться так:

интеграл высчитывается так:

Проще всего сделать проверку, посчитав производную:

Я эту часть снова оставлю вам: вы сами прекрасно справитесь.

Особенную красоту этому методу придаёт простота реализации. Работает он очень хорошо, несмотря на то, что понять, почему это происходит, будет немного сложнее, чем в случае с другими методами.

Вычислять пи этим методом вы можете лёжа на пляже: качество вычислений от этого не пострадает. Разве это не красиво?

Заключение

Существует много других способов вычисления π с использованием моделирования методом Монте-Карло. Мной были выбраны именно эти три способа из-за их непохожести друг на друга: они наглядно демонстрируют, насколько разнообразно моделирование методом Монте-Карло. Вам остаётся лишь выбрать своего фаворита: один из этих трёх методов или какой-то другой.

А какой ваш любимый способ вычисления π?

Видео:Как считали число пи? [Veritasium]Скачать

Вычисление числа пи методом монте карло

Глава 1. Предыстория и определение метода Монте-Карло. 4

Глава 2. Примеры использования метода Монте-Карло. 8

2.1 Простейший пример использования метода Монте-Карло. 8

2.2 Вычисление числа Пи методом Монте-Карло. 8

2.2.1 Постановка задачи для нахождения числа Пи методом Монте-Карло 10

2.2.2 Исходник программы для нахождения числа Пи методом Монте-Карло 10

2.3 Решение задачи аналитически и методом Монте-Карло. 12

Глава 3. Генерация случайных чисел. 17

Список литературы.. 21

Методы Монте-Карло – это общее название группы методов для решения различных задач с помощью случайных последовательностей. Эти методы (как и вся теория вероятностей) выросли из попыток людей улучшить свои шансы в азартных играх. Этим объясняется и тот факт, что название этой группе методов дал город Монте-Карло – столица европейского игорного бизнеса (казино), где играют в рулетку – одно из простейших устройств для получения случайных чисел, на использовании которых основан этот метод.

ЭВМ позволяют легко получать так называемые псевдослучайные числа (при решении задач их применяют вместо случайных чисел); это привело к широкому внедрению метода во многие области науки и техники (статистическая физика, теория массового обслуживания, теория игр и др.).

Глава 1. Предыстория и определение метода Монте-Карло

Создателями метода статистических испытаний (метода Монте-Карло) считают американских математиков Д. Неймана и С. Улама. В 1944 году, в связи с работами по созданию атомной бомбы Нейман предложил широко использовать аппарат теории вероятностей для решения прикладных задач с помощью ЭВМ. Первая работа, где этот вопрос систематически излагался, принадлежит Метрополису и Уламу.

Первоначально метод Монте-Карло использовался главным образом для решения задач нейтронной физики, где традиционные численные методы оказались малопригодными. Далее его влияние распространилось на широкий класс задач статистической физики, очень разных по своему содержанию. К разделам науки, где все в большей мере используется метод Монте-Карло, следует отнести задачи теории массового обслуживания, задачи теории игр и математической экономики, задачи теории передачи сообщений при наличии помех и ряд других.

Аналитические методы дают решение задачи либо в виде формулы, либо в виде разложения в ряды или интегралы по полному набору собственных функций какого-нибудь оператора.

Классические численные методы дают приближенную схему решения задачи, связанную, обычно с разбиением пространства на строго определенные клетки и заменой интегрирования суммированием и дифференцирования – конечными разностями.

Основными недостатками аналитических методов являются:

§ Недостаточная универсальность основных способов решения. Например, способ разложения в ряд по собственным функциям практически не работают для тех дифференциальных уравнений в частных производных, где переменные не разделяются, и так далее.

§ Крайне ограниченный набор геометрических условий, для которых возможно решение задачи. Даже сочетание простых, но разнотипных поверхностей делает задачу неразрешимой.

§ Невозможность расчета физического процесса, вероятностное описание которого известно, но выражение в виде уравнения крайне затруднительно.

Классические численные методы исправляют часть этих недостатков, но зато добавляют свои собственные. Они не страшатся сложной геометрии задач, однако:

§ Они чрезвычайно громоздки. Объем промежуточной информации трудно вместить даже в память современного компьютера.

§ Оценка погрешности решения представляет намного более трудную процедуру, чем сам процесс решения. Зачастую она просто невозможна.

Метод статистических испытаний свободен от всех этих недостатков.

Метод Монте-Карло можно определить как метод моделирования случайной величины с целью вычисления характеристик их распределений. Это численный метод решения математических задач при помощи моделирования случайных величин.

Задача метода Монте-Карло после получения ряда реализаций интересующей нас случайной величины заключается в получении некоторых сведений о ее распределении, т. е. является типичной задачей математической статистики.

Итак, сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую случайную величину X, математическое ожидание которой равно а:

Практически же поступают так: производят N испытаний, в результате которых получают N возможных значений X, вычисляют их среднее арифметическое и принимают его в качестве оценки (приближенного значения) A’ искомого числа A.

Как правило, составляется программа для осуществления одного случайного испытания. Погрешность вычислений, как правило, пропорциональна , где D – некоторая постоянная.

Это значит, что N должно быть велико, поэтому метод существенно опирается на возможности ЭВМ. Ясно, что добиться таким путем высокой точности невозможно. Это один из недостатков метода. Во многих задачах удается значительно увеличить точность, выбрав способ расчета, которому соответствует значительно меньшее D.

Поскольку метод Монте-Карло требует проведения большого числа испытаний, его часто называют методом статистических испытаний. Теория этого метода указывает, как наиболее целесообразно выбрать случайную величину X, как найти ее возможные значения.

Отыскание возможных значений случайной величины Х (моделирование) называют «разыгрыванием случайной величины».

Метод Монте-Карло позволяет моделировать любой процесс, на протекание которого влияют случайные факторы. Для многих математических задач, не связанных с какими-либо случайностями, можно искусственно придумать вероятностную модель, которая в некоторых случаях является более выгодной.

В отличие от аналитических методов, ищущих решение в виде ряда по собственным функциям, методы Монте-Карло ищут решения в виде статистических сумм. Для их применения достаточно описания вероятностного процесса и не обязательна его формулировка в виде интегрального уравнения; оценка погрешности чрезвычайно проста, их точность слабо зависит от размерности пространства.

Главный недостаток метода Монте-Карло заключается в том, что, являясь в основном численным методом, он не может заменить аналитические методы при расчете существенно новых явлений, где, прежде всего, нужно раскрытие качественных закономерностей.

Преимущество метода Монте-Карло состоит в том, что он способен “сработать” там, где не справляются другие методы.

Аналитические методы исследования позволяют существенно уменьшить погрешность метода Монте-Карло и могут поднять его до уровня получения качественных закономерностей. Синтез аналитических и статистических методов может свести D к очень малой величине, следовательно, уменьшить погрешность.

Приведем примеры задач, решаемых методом Монте-Карло:

– расчет системы массового обслуживания;

– расчет качества и надежности изделий;

– теория передачи сообщений;

– вычисление определенного интеграла;

– задачи вычислительной математики;

– задачи нейтронной физики и другие.

Видео:Длина окружности. Математика 6 класс.Скачать

2.1 Простейший пример использования метода Монте-Карло

Предположим, что нам нужно определить площадь плоской фигуры, расположенной внутри единичного квадрата, т. е. квадрата, сторона которого равна единице (рис. 1). Выберем внутри квадрата наугад N точек. Обозначим через M количество точек, попавших при этом внутрь фигуры. Тогда площадь фигуры приближенно равна отношению . Отсюда, чем больше N, тем больше точность такой оценки.

Рисунок 1. Площадь фигуры приближенно равна, отношению числа точек попавших в фигуру к числу всех точек.

Видео:Число Пи-здесь. Объяснение математического смысла.Скачать

2.2 Вычисление числа Пи методом Монте-Карло

Попробуем построить метод Монте-Карло для решения задачи о вычислении числа Пи. Для этого рассмотрим четверть круга единичного радиуса (рис. 2). Площадь круга равна , очевидно, площадь четверти круга равна:

.

Зная, что радиус круга равен 1, получим:

Рисунок 2. Нахождение числа Пи методом Монте-Карло.

Площадь же всего единичного квадрата OABC равна 1. Будем случайным образом выбирать точки внутри квадрата OABC. Координаты точек должны быть, и . Теперь подсчитаем количество точек таких, что , т. е. те точки, которые попадают внутрь круга.

Пусть всего было испытано N точек, и из них M попало в круг. Рассмотрим отношение количества точек, попавших в круг, к общему количеству точек (M/N). Очевидно, что чем больше случайных точек мы испытаем, тем это отношение будет ближе к отношению площадей четверти круга и квадрата. Таким образом, имеем, что, для достаточно больших N, верно равенство:

.

Из полученного равенства:

.

Итак, мы построили метод Монте-Карло для вычисления числа Пи. Опять перед нами стоит вопрос о том, какое именно количество точек N нужно испытать для того, чтобы получить Пи с предсказуемой точностью? Вопрос о точности вычислений с помощью методов Монте-Карло рассматривается в традиционных курсах теории вероятностей, и мы не будем останавливаться на нем подробно. Можно отметить лишь, что точность вычислений очень сильно зависит от качества используемого генератора псевдослучайных чисел. Другими словами, точность тем выше, чем более равномерно случайные точки распределяются по единичному квадрату.

2.2.1 Постановка задачи для нахождения числа Пи методом Монте-Карло

Для проверки формулы [1], была написана программа в среде программирования Турбо Паскаль. В программе нужно ввести число K – количество испытаний и число N – количество испытываемых точек. Для координат точек (X, Y) используется генератор случайных чисел. Результаты всех испытаний усредняются.

Предположим, что перед Вами встала такая задача, как приближенное вычисление числа Пи. Например, вы получили ее на собеседовании. Метод Монте-Карло довольно прост в понимании и реализации, поэтому именно его мы и выбрали в качестве темы данной статьи.

Итак, суть метода сводится к следующему. Допустим, что у нас есть квадрат со стороной a = 2R. Мы вписываем в него окружность и начинаем генерировать точки из диапазона [-a; a]. Считаем количество точек, попавших в круг. Это значение нам пригодится. Если вы вдруг подзабыли курс математики, то напомним, что окружность описывается уравнением x 2 + y 2 = r 2 . Соответственно, точка находится внутри окружности, если значение x 2 + y 2 2 .

Площадь круга рассчитывается по формуле Sкр. = pi * R 2 .

Площадь квадрата равна Sкв. = a 2 = (2R) 2 = 4R 2 .

Вероятность попадания точки в круг равна отношению площадей квадрата и круга:

p = Sкр./Sкв. = pi * R 2 / 4R 2 = pi/4.

В итоге получается, что при большом количестве точек вероятность попадания в круг можно посчитать как отношение точек, попавших в круг и общего количества точек.

И в итоге мы получаем окончательную формулу для вычисления числа Пи при помощи метода Монте-Карло:

Теперь реализуем данный метод на языке Java. Радиус возьмем единичный.

Существует много способов вычисления числа Пи. Самым простым и понятным является численный метод Монте-Карло, суть которого сводится к простейшему перебору точек на площади. Суть расчета заключается в том, что мы берем квадрат со стороной a = 2 R, вписываем в него круг радиусом R. И начинаем наугад ставить точки внутри квадрата. Геометрически, вероятность P₁ того, чтот точка попадет в круг, равна отношению площадей круга и квадрата:
P₁=S_круг / S_{квадрата} = πR 2 / a 2 = πR 2 / (2 R ) 2 = πR 2 / (2 R) 2 = π / 4 (1)
Выглядит это так:

Вероятность попадания точки в круг можно также посчитать после численного эксперимента ещё проще: посчитать количество точек, попавших в круг, и поделить их на общее количество поставленных точек:
P₂=N_{попавших в круг} / N_точек; (2)
Так, при большом количестве точек в численном эксперименте вероятности должны вести себя cледующим образом:
lim_(Nточек→∞)⁡(P2-P1)=0; (3)
Следовательно:
π / 4 = N_{попавших в круг} / N_точек; (4)
π =4 Nпопавших в круг / N_точек; (5)
НО! При моделировании мы применяем псевдослучайные числа, которые не являются случайным процессом.
Поэтому, выражение (5), к сожалению, строго не выполняется. Логичны вопросы, каковы оптимальные размеры квадрата и как много нужно применить точек?
Чтобы это выяснить, я написал такую программу:

Программа выводит значения числа Пи в зависимости от радиуса и количества точек. Единственное, что остается читателю, это скомпилировать её самостоятельно и запустить с параметрами, которые желает он.

Приведу лишь одну таблицу с полученными значениями:

Если что, значение числа Пи можно посмотреть с точностью до определенного знака здесь.
Источник картинки — википедия.

Видео:Как быстро вычислить любую цифру числа π // Vital MathСкачать

Вычисление числа Пи методом Монте-Карло

Существует много способов вычисления числа Пи. Самым простым и понятным является численный метод Монте-Карло, суть которого сводится к простейшему перебору точек на площади. Суть расчета заключается в том, что мы берем квадрат со стороной a = 2 R, вписываем в него круг радиусом R. И начинаем наугад ставить точки внутри квадрата. Геометрически, вероятность P₁ того, чтот точка попадет в круг, равна отношению площадей круга и квадрата:
P₁=S_круг / S_{квадрата} = πR 2 / a 2 = πR 2 / (2 R ) 2 = πR 2 / (2 R) 2 = π / 4 (1)
Выглядит это так:

Вероятность попадания точки в круг можно также посчитать после численного эксперимента ещё проще: посчитать количество точек, попавших в круг, и поделить их на общее количество поставленных точек:
P₂=N_{попавших в круг} / N_точек; (2)
Так, при большом количестве точек в численном эксперименте вероятности должны вести себя cледующим образом:
lim_{(Nточек→∞)⁡}(P2-P1)=0; (3)
Следовательно:
π / 4 = N_{попавших в круг} / N_точек; (4)
π =4 Nпопавших в круг / N_точек; (5)
НО! При моделировании мы применяем псевдослучайные числа, которые не являются случайным процессом.
Поэтому, выражение (5), к сожалению, строго не выполняется. Логичны вопросы, каковы оптимальные размеры квадрата и как много нужно применить точек?
Чтобы это выяснить, я написал такую программу:

Программа выводит значения числа Пи в зависимости от радиуса и количества точек. Единственное, что остается читателю, это скомпилировать её самостоятельно и запустить с параметрами, которые желает он.

Приведу лишь одну таблицу с полученными значениями:

Если что, значение числа Пи можно посмотреть с точностью до определенного знака здесь.
Источник картинки — википедия.

💡 Видео

Топ метод вычисления интегралов. Формула интегрирования по частям. Высшая математикаСкачать

Число Пи не перестает удивлять!Скачать

Число Пи: как найти его с точностью до 50 знака?Скачать

Поясняю за число ПиСкачать

e, π и другие иррациональности | Ботай со мной #047 | Борис Трушин |Скачать

КАК ЗАПОМНИТЬ ЧИСЛО π (ПИ)? #егэ #математика #огэ #пи #егэпоматематике #задача #егэ2022 #shortsСкачать

Что такое число Пи? Кто его изобрел и почему оно так важноСкачать

Как π чуть не стало 6,283185... [3Blue1Brown]Скачать

Вычисление числа ПИ методом Монте-КарлоСкачать

07. Быстрое вычисление числа π по ЭйлеруСкачать

#182. Постижение числа π (feat. Алексей Савватеев)Скачать

Радианы, градусы, число пиСкачать

Загадки числа ПиСкачать

Число Пи метод Монте Карло алгоритм СЧ ДьяконоваСкачать

ЧЕМУ РАВНО ЧИСЛО ПИ? [ Четыре способа вычисления числа пи ]Скачать