Сторона квадрата равна 24 найдите радиус окружности описанной

Радиус окружности, описанной около квадрата, равен Найдите радиус окружности, вписанной в этот квадрат.

Пусть a — сторона квадрата. Радиус окружности, описанной около квадрата, равен

Тогда сторона квадрата равна

Радиус вписанной окружности (r) равен половине стороны квадрата. Получаем:

Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

Сторона квадрата равна 24 найдите радиус окружности описанной

Вопрос по геометрии:

Сторона квадрата 24 корня из 2.Найдите радиус , описанной около него окружности.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Квадрат равен 24 найдите радиус вписанной окружности

Видео:Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.Скачать

Квадрат равен 24 найдите радиус вписанной окружности

Радиус окружности, описанной около квадрата, равен Найдите радиус окружности, вписанной в этот квадрат.

Пусть a — сторона квадрата. Радиус окружности, описанной около квадрата, равен

Тогда сторона квадрата равна

Радиус вписанной окружности (r) равен половине стороны квадрата. Получаем:

Видео:Геометрия Один из углов ромба равен 60, а большая диагональ равна 24 см. Найдите радиус окружностиСкачать

Сторона квадрата равна 24 (см, м, дм), найдите его радиус вписанной окружности. Калькулятор онлайн с формулами расчётов.

Введите данные:

Достаточно ввести только одно значение, остальное калькулятор посчитает сам.

Округление:

Cторона, диаметр вписанной окружности (L) = 24

Диагональ, диаметр описанной окружности (M) = (sqrt >) = (sqrt >) = 33.94

Радиус вписанной окружности (R1) = (frac ) = (frac ) = 12

Радиус описанной окружности (R2) = (frac ) = (frac ) = 16.97

Периметр (P) = (L*4) = (24*4) = 96

Видео:СТОРОНА КВАДРАТА через РАДИУС вписанной и описанной окружностейСкачать

Квадрат. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Свойства квадрата

• Длины всех сторон квадрата равны.
• Все углы квадрата прямые.
• Диагонали квадрата равны.
• Диагонали пересекаются под прямым углом.
• Диагонали квадрата являются биссектрисами углов.
• Диагонали квадрата точкой пересечения делятся пополам.

Изложеннные свойства изображены на рисунках ниже:

Видео:2092 найдите радиус окружности описанной около квадрата со стороной 27 корней из 2Скачать

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

(1)

Из равенства (1) найдем d:

.

(2)

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

Окружность, вписанная в квадрат

Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

(3)

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

(4)

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Окружность, описанная около квадрата

Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Видео:Задача 6 №27917 ЕГЭ по математике. Урок 134Скачать

Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

(5)

Из формулы (5) найдем R:

(6)

или, умножая числитель и знаменатель на , получим:

.

(7)

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Видео:Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

.

(8)

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Видео:Задание 16 ОГЭ по математике. Окружность описана около квадратаСкачать

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

(9)

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Видео:Радиус описанной окружностиСкачать

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.

Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

(10)

Так как AD и BC перпендикулярны, то

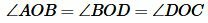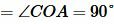(11)

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

(12)

Эти реугольники также равнобедренные. Тогда

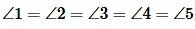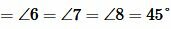(13)

Из (13) следует, что

(14)

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).

🎦 Видео

Задание 24 Радиус окружности вписанной в прямоугольный треугольникСкачать

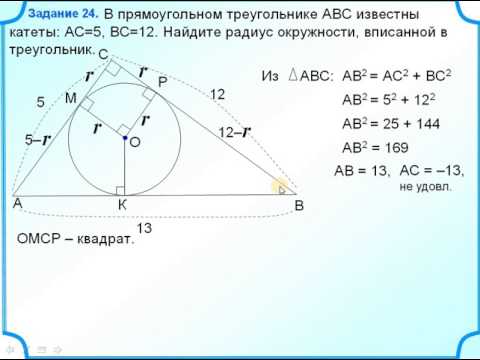
Задание 24 ОГЭ по математике #7Скачать

Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Задача 6 №27923 ЕГЭ по математике. Урок 140Скачать

Задача 6 №27892 ЕГЭ по математике. Урок 126Скачать