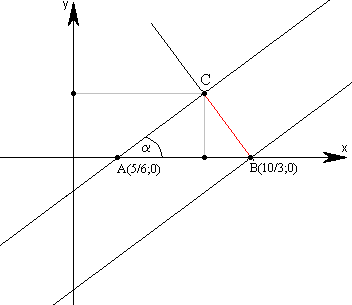
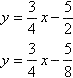
Проведем, допустим, этот перпендикуляр. И обозначим треугольник АВС. В нем:
tg? = ? — коэффициент при х
Для нахождения d нам необходим sin? . Для нахождения синуса используем
формулы 5 и 6
- Расстояние между прямыми в пространстве онлайн
- Предупреждение
- Расстояние между прямыми в пространстве − теория, примеры и решения
- 1. Расстояние между параллельными прямыми в пространстве
- 2. Расстояние между скрещивающимися прямыми в пространстве
- Расстояние между двумя параллельными прямыми: определение и примеры нахождения
- Расстояние между двумя параллельными прямыми: определение
- Нахождение расстояния между параллельными прямыми
- 📽️ Видео
Видео:Расстояние между параллельными прямымиСкачать

Расстояние между прямыми в пространстве онлайн
С помощю этого онлайн калькулятора можно найти расстояние между прямыми в пространстве. Дается подробное решение с пояснениями. Для вычисления расстояния между прямыми в пространстве, задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Расстояние между прямыми в пространстве − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:
 . . | (1) |
 , , | (2) |
Прямые (1) и (2) в пространстве могут совпадать, быть паралленьными, пересекаться, или быть скрещивающимся. Если прямые в пространстве пересекаются или совпадают, то расстояние между ними равно нулю. Мы рассмотрим два случая. Первый − прямые параллельны, и второй − прямые скрещиваются. Остальные являются частыми случаями. Если при вычислении расстояния между параллельными прямыми мы получим расстояние равным нулю, то это значит, что эти прямые совпадают. Если же расстояние между скрещивающимися прямыми равно нулю, то эти прямые пересекаются.
1. Расстояние между параллельными прямыми в пространстве
Рассмотрим два метода вычисления расстояния между прямыми.
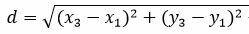  |
которое и является расстоянием между прямыми L1 и L2 (Рис.1).
 |
Пример 1. Найти расстояние между прямыми L1 и L2:
 | (3) |
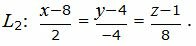 | (4) |
| q1=<m1, p1, l1>= |
| q2=<m2, p2, l2>= |
Найдем проекцию точки M1 на прямую L2. Для этого построим плоскость α, проходящей через точку M1 и перпендикулярной прямойL2.
Для того, чтобы плоскость α было перепендикулярна прямой L2, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L2, т.е. в качестве нормального вектора плоскости α можно взять направляющий вектор прямой L2. Тогда уравнение искомой плоскости, проходящей через точку M1(x1, y1, z1) имеет следующий вид:
| m2<x−x1)+p2(y−y1)+ l2(z−z1)=0 | (5) |
| 2(x−1)−4(y−2)+ 8(z−1)=0 |
После упрощения получим уравнение плоскости, проходящей через точку M1 и перпендикулярной прямой L2:
| 2x−4y+ 8z−2=0 | (6) |
Найдем точку пересечения прямой L2 и плоскости α, для этого построим параметрическое уравнение прямой L2.
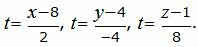 |
Выразив переменные x, y, z через параметр t, получим параметрическое уравнение прямой L2:
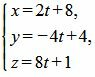 | (7) |
Чтобы найти точку пересечения прямой L2 и плоскости α, подставим значения переменных x, y, z из (7) в (6):
 |
Решив уравнение получим:
 | (8) |
Подставляя полученное значение t в (7), получим точку пересеченияпрямой L2 и плоскости α:
 |
Остается найти расстояние между точками M1 и M3:
 |
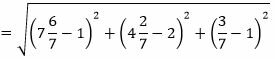  |
Ответ: Расстояние между прямыми L1 и L2 равно d=7.2506.
Метод 2. Найдем расстояние между прямыми L1 и L2 (уравнения (1) и (2)). Во первых, проверяем параллельность прямых L1 и L2. Если направляющие векторы прямых L1 и L2 коллинеарны, т.е. если существует такое число λ, что выполнено равенство q1=λq2, то прямые L1 и L2 параллельны.
Данный метод вычисления расстояния между параллельными векторами основана на понятии векторного произведения векторов. Известно, что норма векторного произведения векторов 
 |
Вычислим координаты вектора 
 |
Вычислим векторное произведение векторов 
 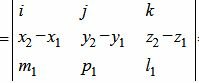 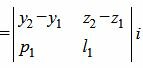  |
Вычисляя определители второго порядка находим координаты вектора c:
Далее находим площадь параллелограмма:
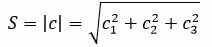 . . |
Расстояние между прямыми L1 и L2 равно:
 , , |
 , , |
Пример 2. Решим пример 1 методом 2. Найти расстояние между прямыми
 | (25) |
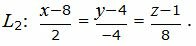 | (26) |
| q1=<m1, p1, l1>= |
| q2=<m2, p2, l2>= |
Векторы q1 и q2 коллинеарны. Следовательно прямые L1 и L2 параллельны. Для вычисления расстояния между параллельными прямыми воспользуемся векторным произведением векторов.
Построим вектор 
Вычислим векторное произведение векторов 

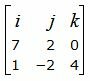 |
Вычислим определитель этой матрицы, разложив ее по первой строке. Результатом этих вычислений получим векторное произведение векторов 
   |
Таким образом, результатом векторного произведения векторов 
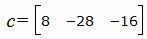 |
Поскольку векторное произведение векторов 
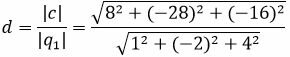  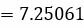 |
Ответ: Расстояние между прямыми L1 и L2 равно d=7.25061.
2. Расстояние между скрещивающимися прямыми в пространстве
Пусть задана декартова прямоугольная симтема координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 (уравнения (1) и (2)).
Пусть прямые L1 и L2 не параллельны (паралельные прямые мы расстотрели в предыдущем параграфе). Чтобы найти расстояние между прямыми L1 и L2 нужно построить параллельные плоскости α1 и α2 так, чтобы прямая L1 лежал на плоскости α1 а прямая L2 − на плоскости α2. Тогда расстояние между прямыми L1 и L2 равно расстоянию между плоскостями L1 и L2 (Рис. 3).
 |
Поскольку плоскость α1, проходит через прямую L1, то он проходит также через M1(x1, y1, z1). Следовательно справедливо следующее равенство:
| A1x1+B1y1+C1z1+D1=0. | (27) |
где n1=<A1, B1, C1> − нормальный вектор плоскости α1. Для того, чтобы плоскость α1 проходила через прямую L1, нормальный вектор n1 должен быть ортогональным направляющему вектору q1 прямой L1, т.е. скалярное произведение этих векторов должен быть равным нулю:
| A1m1+B1p1+C1l1=0. | (28) |
Так как плоскость α1 должна быть параллельной прямой L2, то должна выполнятся условие:
| A1m2+B1p2+C1l2=0. | (29) |
Решая систему линейных уравнений (27)−(29), с тремя уравнениями и четыремя неизвестными A1, B1, C1, D1, и подставляя в уравнение
| A1x+B1y+C1z+D1=0. | (30) |
получим уравнение плоскости α1. (Как построить уравнение плоскости, проходящей через прямую, параллельно другой прямой подробно изложено здесь).
Аналогичным образом находим уравнение плоскости α2:
| A2x+B2y+C2z+D2=0. | (31) |
Плоскости α1 и α2 параллельны, следовательно полученные нормальные векторыn1=<A1, B1, C1> и n2=<A2, B2, C2> этих плоскостей коллинеарны. Если эти векторы не равны, то можно умножить (31) на некторое число так, чтобы полученный нормальный вектор n2 совпадал с нормальным вектором уравнения (30).
Тогда расстояние между параллельными плоскостями вычисляется формулой:
 . . |
Полученное расстояние между плоскостями α1 и α2 является также расстоянием между прямыми L1 и L2.
Пример 3. Найти расстояние между прямыми
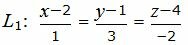 | (32) |
 | (33) |
Построим плоскость α1, проходящую через прямую L1, параллельно прямой L2.
Поскольку плоскость α1 проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(2, 1, 4) и нормальный вектор n1=<m1, p1, l1> плоскости α1 перпендикулярна направляющему вектору q1 прямой L1. Тогда уравнение плоскости должна удовлетворять условию:
| A1x1+B1y1+C1z1+D1=0. | (34) |
а условие параллельности прямой L1 и искомой плоскости α1 представляется следующим условием:
| A1m1+B1p1+C1l1=0. | (35) |
Так как плоскость α1 должна быть параллельной прямой L2, то должна выполнятся условие:
| A1m2+B1p2+C1l2=0. | (36) |
| A1·2+B1·1+C1·4+D1=0. | (37) |
| A1·1+B1·3+C1·(−2)=0. | (38) |
| A1·2+B1·(−3)+C1·7=0. | (39) |
Представим эти уравнения в матричном виде:
 | (40) |
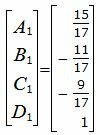 | (41) |
Искомая плоскость может быть представлена формулой:
| A1x+B1y+C1z+D1=0. | (42) |
 |
Упростим уравнение, умножив на число 17.
 | (43) |
Построим плоскость α2, проходящую через прямую L2, параллельно прямой L1.
Поскольку плоскость α2 проходит через прямую L2 , то она проходит также через точку M2(x2, y2, z2)=M2(6, −1, 2) и нормальный вектор n2=<m2, p2, l2> плоскости α2 перпендикулярна направляющему вектору q2 прямой L2. Тогда уравнение плоскости должна удовлетворять условию:
| A2x2+B2y2+C2z2+D2=0. | (44) |
а условие параллельности прямой L2 и искомой плоскости α2 представляется следующим условием:
| A2m2+B2p2+C2l2=0. | (45) |
Так как плоскость α2 должна быть параллельной прямой L1, то должна выполнятся условие:
| A2m1+B2p1+C2l1=0. | (46) |
| A1·6+B1·(−1)+C1·2+D1=0. | (47) |
| A1·2+B1·(−3)+C1·7=0. | (48) |
| A1·1+B1·3+C1·(−2)=0. | (49) |
Представим эти уравнения в матричном виде:
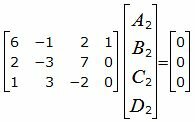 | (50) |
 | (51) |
Искомая плоскость может быть представлена формулой:
| A2x+B2y+C2z+D2=0. | (52) |
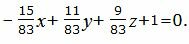 |
Упростим уравнение, умножив на число −83.
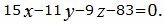 | (53) |
Расстояние между построенными плоскостями (43) и (53) будет расстоянием между прямыми (1) и (2).
Запишем формулы уравнений плоскостей α1 и α2 :
| A1x+B1y+C1z+D1=0. |
| A2x+B2y+C2z+D2=0. |
Поскольку нормальные векторы плоскостей α1 и α2 совпадают, то можно найти расстояние между плоскостями α1 и α2, используя следующую формулу:
 | (54) |
 |
Упростим и решим:
 |
Расстояние между прямыми равно: d=4.839339
Видео:19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Расстояние между двумя параллельными прямыми: определение и примеры нахождения
В материале этой статьи разберем вопрос нахождения расстояния между двумя параллельными прямыми, в частности, при помощи метода координат. Разбор типовых примеров поможет закрепить полученные теоретические знания.
Видео:Геометрия 7 класс (Урок№26 - Расстояние от точки до прямой. Расстояние между параллельными прямыми.)Скачать

Расстояние между двумя параллельными прямыми: определение
Расстояние между двумя параллельными прямыми – это расстояние от некоторой произвольной точки одной из параллельных прямых до другой прямой.
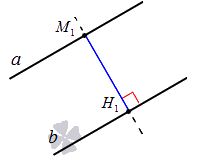
Приведем иллюстрацию для наглядности:
На чертеже изображены две параллельные прямые a и b . Точка М 1 принадлежит прямой a , из нее опущен перпендикуляр на прямую b . Полученный отрезок М 1 Н 1 и есть расстояние между двумя параллельными прямыми a и b .
Указанное определение расстояния между двумя параллельными прямыми справедливо как на плоскости, так и для прямых в трехмерном пространстве. Кроме того, данное определение взаимосвязано со следующей теоремой.
Когда две прямые параллельны, все точки одной из них равноудалены от другой прямой.
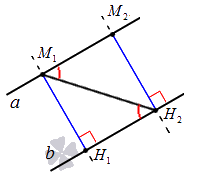
Пусть нам заданы две параллельные прямые a и b . Зададим на прямой а точки М 1 и М 2 , опустим из них перпендикуляры на прямую b , обозначив их основания соответственно как Н 1 и Н 2 . М 1 Н 1 – это расстояние между двумя параллельными прямыми по определению, и нам необходимо доказать, что | М 1 Н 1 | = | М 2 Н 2 | .
Пусть будет также существовать некоторая секущая, которая пересекает две заданные параллельные прямые. Условие параллельности прямых, рассмотренное в соответствующей статье, дает нам право утверждать, что в данном случае внутренние накрест лежащие углы, образованные при пересечении секущей заданных прямых, являются равными: ∠ M 2 M 1 H 2 = ∠ H 1 H 2 M 1 . Прямая М 2 Н 2 перпендикулярна прямой b по построению, и, конечно, перпендикулярна прямой a . Получившиеся треугольники М 1 Н 1 Н 2 и М 2 М 1 Н 2 являются прямоугольными и равными друг другу по гипотенузе и острому углу: М 1 Н 2 – общая гипотенуза, ∠ M 2 M 1 H 2 = ∠ H 1 H 2 M 1 . Опираясь на равенство треугольников, мы можем говорить о равенстве их сторон, т.е.: | М 1 Н 1 | = | М 2 Н 2 | . Теорема доказана.
Отметим, что расстояние между двумя параллельными прямыми – наименьшее из расстояний от точек одной прямой до точек другой.
Видео:38. Расстояние от точки до прямой. Расстояние между параллельными прямымиСкачать

Нахождение расстояния между параллельными прямыми
Мы уже выяснили, что, по сути, чтобы найти расстояние между двумя параллельными прямыми, необходимо определить длину перпендикуляра, опущенного из некой точки одной прямой на другую. Способов, как это сделать, несколько. В каких-то задачах удобно воспользоваться теоремой Пифагора; другие предполагают использование признаков равенства или подобия треугольников и т.п. В случаях, когда прямые заданы в прямоугольной системе координат, возможно вычислить расстояние между двумя параллельными прямыми, используя метод координат. Рассмотрим его подробнее.
Зададим условия. Допустим, зафиксирована прямоугольная система координат, в которой заданы две параллельные прямые a и b . Необходимо определить расстояние между заданными прямыми.
Решение задачи построим на определении расстояния между параллельными прямыми: для нахождения расстояния между двумя заданными параллельными прямыми необходимо:
— найти координаты некоторой точки М 1 , принадлежащей одной из заданных прямых;
— произвести вычисление расстояния от точки М 1 до заданной прямой, которой эта точка не принадлежит.
Опираясь на навыки работы с уравнениями прямой на плоскости или в пространстве, определить координаты точки М 1 просто. При нахождении расстояния от точки М 1 до прямой пригодится материал статьи о нахождении расстояния от точки до прямой.
Вернемся к примеру. Пусть прямая a описывается общим уравнением A x + B y + C 1 = 0 , а прямая b – уравнением A x + B y + C 2 = 0 . Тогда расстояние между двумя заданными параллельными прямыми возможно вычислить, используя формулу:
M 1 H 1 = C 2 — C 1 A 2 + B 2
Выведем эту формулу.
Используем некоторую точку М 1 ( x 1 , y 1 ) , принадлежащую прямой a . В таком случае координаты точки М 1 будут удовлетворять уравнению A x 1 + B y 1 + C 1 = 0 . Таким образом, справедливым является равенство: A x 1 + B y 1 + C 1 = 0 ; из него получим: A x 1 + B y 1 = — C 1 .
Когда С 2 0 , нормальное уравнение прямой b будет иметь вид:
A A 2 + B 2 x + B A 2 + B 2 y + C 2 A 2 + B 2 = 0
При С 2 ≥ 0 нормальное уравнение прямой b будет выглядеть так:
A A 2 + B 2 x + B A 2 + B 2 y — C 2 A 2 + B 2 = 0
И тогда для случаев, когда С 2 0 , применима формула: M 1 H 1 = A A 2 + B 2 x 1 + B A 2 + B 2 y 1 + C 2 A 2 + B 2 .
А для С 2 ≥ 0 искомое расстояние определяется по формуле M 1 H 1 = — A A 2 + B 2 x 1 — B A 2 + B 2 y 1 — C 2 A 2 + B 2 = = A A 2 + B 2 x 1 + B A 2 + B 2 y 1 + C 2 A 2 + B 2
Таким образом, при любом значении числа С 2 длина отрезка | М 1 Н 1 | (от точки М 1 до прямой b ) вычисляется по формуле: M 1 H 1 = A A 2 + B 2 x 1 + B A 2 + B 2 y 1 + C 2 A 2 + B 2
Выше мы получили: A x 1 + B y 1 = — C 1 , тогда можем преобразовать формулу: M 1 H 1 = — C 1 A 2 + B 2 + C 2 A 2 + B 2 = C 2 — C 1 A 2 + B 2 . Так мы, собственно, получили формулу, указанную в алгоритме метода координат.
Разберем теорию на примерах.
Заданы две параллельные прямые y = 2 3 x — 1 и x = 4 + 3 · λ y = — 5 + 2 · λ . Необходимо определить расстояние между ними.
Решение
Исходные параметрические уравнения дают возможность задать координаты точки, через которую проходит прямая, описываемая параметрическими уравнениями. Таким образом, получаем точку М 1 ( 4 , — 5 ) . Требуемое расстояние – это расстояние между точкой М 1 ( 4 , — 5 ) до прямой y = 2 3 x — 1 , произведем его вычисление.
Заданное уравнение прямой с угловым коэффициентом y = 2 3 x — 1 преобразуем в нормальное уравнение прямой. С этой целью сначала осуществим переход к общему уравнению прямой:
y = 2 3 x — 1 ⇔ 2 3 x — y — 1 = 0 ⇔ 2 x — 3 y — 3 = 0
Вычислим нормирующий множитель: 1 2 2 + ( — 3 ) 2 = 1 13 . Умножим на него обе части последнего уравнения и, наконец, получим возможность записать нормальное уравнение прямой: 1 13 · 2 x — 3 y — 3 = 1 13 · 0 ⇔ 2 13 x — 3 13 y — 3 13 = 0 .
При x = 4 , а y = — 5 вычислим искомое расстояние как модуль значения крайнего равенства:
2 13 · 4 — 3 13 · — 5 — 3 13 = 20 13
Ответ: 20 13 .
В фиксированной прямоугольной системе координат O x y заданы две параллельные прямые, определяемые уравнениями x — 3 = 0 и x + 5 0 = y — 1 1 . Необходимо найти расстояние между заданными параллельными прямыми.
Решение
Условиями задачи определено одно общее уравнение, задаваемое одну из исходных прямых: x-3=0. Преобразуем исходное каноническое уравнение в общее: x + 5 0 = y — 1 1 ⇔ x + 5 = 0 . При переменной x коэффициенты в обоих уравнениях равны (также равны и при y – нулю), а потому имеем возможность применить формулу для нахождения расстояния между параллельными прямыми:
M 1 H 1 = C 2 — C 1 A 2 + B 2 = 5 — ( — 3 ) 1 2 + 0 2 = 8
Ответ: 8 .
Напоследок рассмотрим задачу на нахождение расстояния между двумя параллельными прямыми в трехмерном пространстве.
В прямоугольной системе координат O x y z заданы две параллельные прямые, описываемые каноническими уравнениями прямой в пространстве: x — 3 1 = y — 1 = z + 2 4 и x + 5 1 = y — 1 — 1 = z — 2 4 . Необходимо найти расстояние между этими прямыми.
Решение
Из уравнения x — 3 1 = y — 1 = z + 2 4 легко определются координаты точки, через которую проходит прямая, описываемая этим уравнением: М 1 ( 3 , 0 , — 2 ) . Произведем вычисление расстояния | М 1 Н 1 | от точки М 1 до прямой x + 5 1 = y — 1 — 1 = z — 2 4 .
Прямая x + 5 1 = y — 1 — 1 = z — 2 4 проходит через точку М 2 ( — 5 , 1 , 2 ) . Запишем направляющий вектор прямой x + 5 1 = y — 1 — 1 = z — 2 4 как b → с координатами ( 1 , — 1 , 4 ) . Определим координаты вектора M 2 M → :
M 2 M 1 → = 3 — ( — 5 , 0 — 1 , — 2 — 2 ) ⇔ M 2 M 1 → = 8 , — 1 , — 4
Вычислим векторное произведение векторов :
b → × M 2 M 1 → = i → j → k → 1 — 1 4 8 — 1 — 4 = 8 · i → + 36 · j → + 7 · k → ⇒ b → × M 2 M 1 → = ( 8 , 36 , 7 )
Применим формулу расчета расстояния от точки до прямой в пространстве:
M 1 H 1 = b → × M 2 M 1 → b → = 8 2 + 36 2 + 7 2 1 2 + ( — 1 ) 2 + 4 2 = 1409 3 2
📽️ Видео
№277. Расстояние между параллельными прямыми а и b равно 3 см, а между параллельными прямымиСкачать

7 класс, 38 урок, Расстояние от точки до прямой. Расстояние между параллельными прямымиСкачать

Определение расстояние между параллельными прямыми (Способ замены плоскостей проекции).Скачать

Геометрия. 7 класс. Расстояние от точки до прямой. Расстояние между параллельными прямыми.Скачать

Расстояние от точки до прямой. Расстояние между параллельными прямыми.Скачать

Расстояние между параллельными плоскостямиСкачать

Расстояние от точки до прямой. Расстояние между параллельными прямыми, 7 классСкачать

Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать

Урок 23. Расстояние между параллельными прямыми (7 класс)Скачать

Расстояние от точки до прямой. Расстояние между параллельными прямымиСкачать

Угол между прямыми в пространстве. 10 класс.Скачать

Расстояние между параллельными и скрещивающимися прямыми | МатематикаСкачать

Видеоурок "Расстояние между прямыми в пространстве"Скачать

Тема 26. Расстояние между параллельными прямымиСкачать

Расстояние между скрещивающимися прямымиСкачать