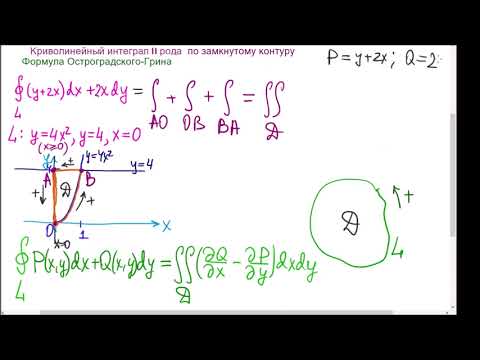
Если дан криволинейный интеграл, а кривая, по которой происходит интегрирование — замкнутая (называется контуром), то такой интеграл называется интегралом по замкнутому контуру и обозначается следующим образом:

Область, ограниченную контуром L обозначим D. Если функции P(x, y) , Q(x, y) и их частные производные 


Таким образом, вычисление криволинейного интеграла по замкнутому контуру сводится к вычислению двойного интеграла по области D.
Формула Грина остаётся справедливой для всякой замкнутой области, которую можно проведением дополнительных линий на конечное число простых замкнутых областей.
Пример 1. Вычислить криволинейный интеграл

если L — контур треугольника OAB , где О(0; 0) , A(1; 2) и B(1; 0) . Направление обхода контура — против часовой стрелки. Задачу решить двумя способами: а) вычислить криволинейные интегралы по каждой стороне треугольника и сложить результаты; б) по формуле Грина.
а) Вычислим криволинейные интегралы по каждой стороне треугольника. Сторона OB находится на оси Ox , поэтому её уравнением будет y = 0 . Поэтому dy = 0 и можем вычислить криволинейный интеграл по стороне OB :
Уравнением стороны BA будет x = 1 . Поэтому dx = 0 . Вычисляем криволинейный интеграл по стороне BA :
Уравнение стороны AO составим, пользуясь формулой уравнения прямой, проходящей через две точки:

Таким образом, dy = 2dx . Вычисляем криволинейный интеграл по стороне AO :
Данный криволинейный интеграл будет равен сумме интегралов по краям треугольника:

б) Применим формулу Грина. Так как 


Как видим, получили один и тот же результат, но по формуле Грина вычисление интеграла по замкнутому контуру происходит значительно быстрее.
Пример 2. Пользуясь формулой Грина, вычислить криволинейный интеграл

где L — контур OAB , OB — дуга параболы y = x² , от точки О(0; 0) до точки A(1; 1) , AB и BO — отрезки прямых, B(0; 1) .
Решение. Так как функции 



Пример 3. Пользуясь формулой Грина, вычислить криволинейный интеграл

Решение. Линия y = 2 − |x| состоит из двух лучей: y = 2 − x , если x ≥ 0 и y = 2 + x , если x .
Имеем функции 



Пример 4. С помощью формулы Грина вычислить криволинейный интеграл

если L — окружность 
Решение. Функции 




Видео:Вычислить интеграл по заданному контуру. Интегрирование по части окружности и по отрезку прямой.Скачать
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Видео:ТФКП. Вычислить интеграл по замкнутому контуру с помощью вычетов. Пример из ДемидовичаСкачать

Глава 4. Интегрирование функций комплексного переменного
Видео:Формула Остроградского - ГринаСкачать
Определение интеграла от функции комплексного переменного
Пусть $[a,b]$ — отрезок на вещественной оси. Образ при непрерывном отображении отрезка $[a,b]$ на комплексную плоскость называется непрерывной кривой: $$ Gamma=. $$ Непрерывная кривая называется кривой Жордана, если указанные отображения взаимно-однозначны, за исключением, может быть, одной точки на кривой, в которую могут отображаться концы отрезка $[a,b]$ (в таком случае кривая — замкнутая). Другими словами, кривая Жордана — непрерывная кривая без самопересечений.
Кривая Жордана называется гладкой, если в каждой ее точке существует касательная (отображение $z(t)$ — непрерывно дифференцируемо, то есть $x,yin C^1[a,b]$, причем $z'(t)neq0$).
Кривая Жордана называется спрямляемой, если она имеет длину. Гладкая кривая имеет длину, но существуют непрерывные кривые, не имеющие длины.
Пусть в области $D$ плоскости $z$ задана непрерывная функция $$ w=f(z)=u(x,y)+ mathbf i v(x,y) $$ и пусть $ell$ — кусочно-гладкая линия с началом в точке $z_0=a$ и концом в точке $z_n=b$, целиком лежащая в области $D$.
Задание начала и конца линии $ell$ ориентирует эту линию, т.е. устанавливает на ней положительное направление.
Линия $ell$ может быть как незамкнутой, так и замкнутой (в последнем случае $z_n=z_0$).
Любым образом разобьем линию $ell$ на $n$ элементарных дуг в направлении от $a$ к $b$ точками $z_1,dots,z_$, где $z_k=x_k+iy_k$. Обозначим $$z_k-z_=Delta z_k=Delta x_k+iDelta y_k,$$ где $$Delta x_k=x_k-x_, ,,Delta y_k=y_k-y_, ,, k=1,dots,n.$$ ($Delta z_k $ — вектор, идущий из точки $z_$ в точку $z_k$, а $|Delta z_k|$ — длина этого вектора, т.е. длина хорды, стягивающей $k$-ую элементарную дугу).
В произвольном месте каждой элементарной дуги $(z_,z_k)$ возьмем соответственно по точке $t_k=xi_k+mathbf i eta_k$.
Составим сумму $$ sumlimits_^n f(t_k)Delta z_k=sumlimits_^n big(u(xi_k,eta_k)Delta x_k-v(xi_k,eta_k)Delta y_kbig)+ $$ $$ +mathbf i sumlimits_^nbig(v(xi_k,eta_k)Delta x_k+u(xi_k,eta_k) Delta y_kbig). $$
Через $max|Delta z_k|$ обозначим наибольшую из величин $|Delta z_k|$. В курсе математического анализа доказывается, что при условии $max|Delta z_k|to0$ (в этом случае $ntoinfty$) обе суммы в правой части формулы для непрерывных функций $u(x,y)$ и $v(x,y)$ $big($непрерывность этих функций следует из непрерывности $f(z)$$big)$ и кусочно-гладкой $ell$ стремятся к конечным пределам, не зависящими ни от способа разбиения $ell$ на элементарные дуги, ни от выбора точек $t_k$.
Эти пределы являются соответственно криволинейными интегралами второго рода $$ lim_(mbox)= intlimits_ u(x,y),dx-v(x,y),dy+mathbf i intlimits_ v(x,y),dx+u(x,y),dy. $$
Следовательно, при $max|Delta z_k|to0$ и сумма в левой части исходной формулы тоже стремится к конечному пределу, не зависящему ни от выбора точек $z_k$, ни от выбора точек $t_k$. Предел этот называется контурным интегралом от функции $f(z)$ вдоль линии $ell$ и обозначается символом $$ intlimits_ f(z),dz=lim_sumlimits_^n f(t_k)Delta z_k=intlimits_ u,dx-v,dy+ mathbf iintlimits_ v,dx+u,dy, $$ т.е. представляется как сумма криволинейных интегралов от вещественной переменной.
Обозначение для интеграла в случае замкнутой кривой: $$ ointlimits_ f(z),dz.$$
При параметрическом задании дуги $ell$: $z(s)=x(s)+iy(s)$, $s_1 0$ такое, что неравенство $|f(z)-f(z_0)| tfkp/chapter4.txt · Последние изменения: 2022/01/14 10:40 — nvr
Видео:ТФКП. Вычисление интегралов с помощью вычетов. Теорема Коши о вычетах. Примеры решенийСкачать

ИНТЕГРИРОВАНИЕ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Видео:ТФКП. Интегральная формула Коши. Примеры решений типовых задач. Решение контурных интегралов.Скачать

Интеграл от функции комплексного переменного
Рассмотрим гладкую кривую Г на комплексной плоскости, заданную параметрическими уравнениями
(определение гладкой кривой дано в начале §8). Как уже отмечалось в § 8, эти уравнения можно записать в компактной форме:
При изменении параметра t от а до /3 соответствующая точка z(t) будет двигаться по кривой Г. Поэтому уравнения (15.1) и (15.2) не только определяют точки кривой Г, но и задают направление обхода этой кривой. Кривая Г с заданным направлением ее обхода называется ориентированной кривой.
Пусть в области D С С задана непрерывная функция /(г) = = и(х, у) + iv(x. у), и пусть кривая Г лежит в D. Чтобы ввести понятие интеграла [ f(z)dz от функции f(z) по кривой Г, определим г
дифференциал dz равенством dz = dx + idy. Подынтегральное выражение преобразуется к виду
Таким образом, интеграл от комплексной функции f(z) по кривой Г естественно определить равенством
в правую часть которого входят два действительных криволинейных интеграла второго рода от действительных функций и и и. Для вычисления этих интегралов следует вместо х и у подставить функции x(t) и t/(/), а вместо dx и dy — дифференциалы этих функций dx = x'(t) dt и dy = y'(t) dt. Тогда интегралы в правой части (15.3) сведутся к двум интегралам от функций действительного переменного t
Теперь мы готовы дать следующее определение.
Интегралом вдоль кривой Г от функции комплексного переменного f(z) называется число, обозначаемое J’ f(z)dz и вычисляемое по
где z(t) = x(t) + iy(t), а ^ t ^ ft, — уравнение кривой Г, a z'(t) = = x'(t) + iy'<t).
Пример 15.1. Вычислить интеграл от функции f(z) = (г — а) п по окружности радиуса г с центром а, направление обхода которой против часовой стрелки.
Р е ш е н и е. Уравнение окружности z — а = г будет z — а = ге а , или
При изменении t. от 0 до 2тг точка z(t.) движется по окружности Г против часовой стрелки. Тогда
Применяя равенство (15.5) и формулу Муавра (2.10), получаем
Мы получили результат, важный для дальнейшего изложения:
Заметим, что значение интеграла не зависит от радиуса г окружности.
П р и мер 15.2. Вычислить интеграл от функции f(z) = 1 но гладкой кривой Г с началом в точке а и концом в точке Ь.
Р е ш е н и е. Пусть кривая Г задается уравнением z(t.) = x(t) + + iy <t), а^ t ^ /3, причем а = -г(а), Ь = z( <3).Используя формулу (15.5), а также формулу Ньютона Лейбница для вычисления интегралов от действительных функций, получим
Мы видим, что интеграл f 1 dz не зависит от вида пути Г, соединяю-
щего точки а и 6, а зависит только от концевых точек.
Изложим вкратце другой подход к определению интеграла от комплексной функции f(z) по кривой, аналогичный определению интеграла от действительной функции по отрезку.
Разобьем кривую Г произвольным образом на п участков точками zq = a, z 1, . zn-ь zn = Ь, занумерованными в направлении движения от начальной точки к конечной (рис. 31). Обозначим z — zo = = Az> . , Zlc — Zk-l = Az/c, zn — Zn— 1 = = Azn. (Число Azk изображается вектором, идущим из точки ziL_i в Zk-) На каждом участке (zk-i,Zk) кривой выберем произвольную точку (д- и составим сумму
Эта сумма называется интегральной суммой. Обозначим через Л длину наибольшего из участков, на которые разбита кривая Г. Рассмотрим последовательность разбиений, для которой Л —? 0 (при этом п -* оо).
П1>едел интегральных сумм, вычисленный при условии, что длина наибольшего из участков разбиения стремится к нулю, называется интегралом от функции /(г) по кривой Г и обозначается Г f(z)dz:
Можно показать, что это определение также приводит нас к формуле (15.3) и, следовательно, эквивалентно определению (15.5), данному выше.
Установим основные свойства интеграла / f(z)dz.
1°. Линейность. Для любых комплексных постоянных а и b
Это свойство следует из равенства (15.5) и соответствующих свойств интеграла по отрезку.
2°. Аддитивность. Если кривая Г разбита на участки Ti м Г2, то
Доказательство. Пусть кривая Г с концами а, Ь разбита точкой с на две части: кривую Гi с концами а, с и кривую Гг с концами с, Ь. Пусть Г задается уравнением z = z(t), а ^ t ^ в. причем а = 2(a), b = z(ft), с = 2(7). Тогда уравнения кривых Г1 и Гг будут z = z(t), где а ^ t ^ 7 для Ti и 7 ^ t ^ /? для Гг. Применяя определение (15.5) и соответствующие свойства интеграла по отрезку, получим
что и требовалось доказать.
Свойство 2° позволяет вычислять интегралы не только по гладким кривым, но также и но кусочно гладким, т.е. кривым, которые можно разбить на конечное число гладких участков.
3°. При изменении направления обхода кривой интеграл меняет знак.
Доказаге л ь с т в о. Пусть кривая Г с концами а и Ь задается уравнением г = г(?), о ^ t ^ $. Кривую, состоящую из тех же точек, что и Г, но отличающуюся от Г направлением обхода (ориентацией), обозначим через Г“. Тогда Г — задается уравнением z = 2i(J)> где z(t) = 2(0 -I— fi — t), Действительно, введем новое переменное г = а + — t. При изменении t от а до (д переменное г изменяется от (5 до а. Следовательно, точка г(т) пробежит кривую Г».
Свойство 3° доказано. (Заметим, что из определения интеграла (15.8) это свойство следует непосредственно: при изменении ориентации кривой все приращения AZk меняют знак.)
4°. Модуль интеграла f f(z)dz не превосходит значения криволи- г
нейного интеграла от модуля функции по длине кривой s (криволинейного интеграла от f(z) первого рода):
Легко видеть, что z[(t) = г’г(т)(а + — t)J = —z’t(t), dt = —dr. Используя определение (15.5) и переходя к переменному г, получим
Доказательство. Воспользуемся тем, что для интеграла по отрезку
(это неравенство сразу следует из определения интеграла по отрезку как предела интегральных сумм). Отсюда и из (15.5) имеем
🎦 Видео
ТФКП. Вычислить интеграл от функции комплексного переменного по данной кривой. Дуга окружности.Скачать

Формула ГринаСкачать

ТФКП. ИНТЕГРАЛ ПО ДУГЕ ОКРУЖНОСТИ от неаналитической функции. Метод замены переменной.Скачать

ТФКП. Вычислить интеграл (сборник задач Чудесенко) Задача 17.Скачать

Попов В. Ю. - ТФКП - Вычисление интегралов от функции комплексной переменной по кривойСкачать
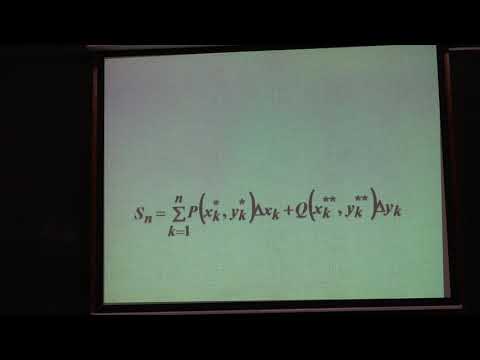
ТФКП. Вычисление контурного интеграла по вычетам.Скачать

Формула ГринаСкачать

Математический анализ, 47 урок, Криволинейные интегралы первого родаСкачать

ТФКП. Интеграл от функции комплексного переменного. Интегралы по различным путям.Скачать

Интеграл по замкнутому контуру.Без формулы ГринаСкачать

Циркуляция векторного поля. Вычисление при при помощи криволинейного интеграла.Скачать

ТФКП. Вычисление интегралов с помощью вычетовСкачать

Математический анализ, 48 урок, Криволинейные интегралы второго родаСкачать

Семинар 8. Криволинейные интегралы.Скачать

Вычисление интегралов с помощью вычетовСкачать