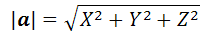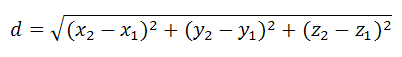Вычисление расстояния между точками вектор (6 видео)

Длина вектора Расстояние между двумя точками в пространстве

Содержание

Длина вектора в пространстве
Расстояние между двумя точками в пространстве
3 комментария
Онлайн калькулятор. Длина отрезка. Расстояние между точками.
Калькулятор для вычисления расстояния между двумя точками
Ввод данных в калькулятор для вычисления расстояния между точками
Дополнительные возможности калькулятора для вычисления расстояния между точками
Теория. Расстояние между точками.
Расчет евклидова расстояния с помощью NumPy
Что такое евклидово расстояние?
Математическая формула
Использование встроенной системы math.dist()
Заключение
💥 Видео

Видео:РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ 10 и 11 классСкачать

Длина вектора в пространстве

Длиной (или модулем) вектора называется расстояние между началом и концом вектора.

Длина вектора a выражается через его координаты следующей формулой:

Пример
Длина вектора $aleft < right>$ равна

Видео:Расстояние между точкамиСкачать

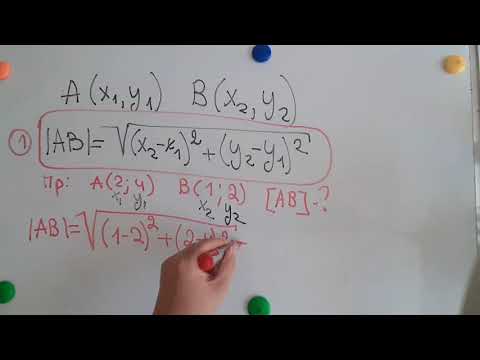
Расстояние между двумя точками в пространстве

Расстояние d между точками в пространстве A₁<x₁;y₁;z₁>, A₂<x₂;y₂;z₂> представляется формулой

Пример
Расстояние между точками A₁ и A₂

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.3 / 5. Количество оценок: 8

Оценок пока нет. Поставьте оценку первым.

Видео:Расстояние между точками. Геометрия 9 класс.Скачать

3 комментария

найти расстояние между точками с(-2;1;-2) д (-1;2;1) м (-1;0;2) н (1;-1;2) найти 3 вектора сд — 2 вектора мн

Видео:Расстояние между двумя точками. Координаты середины отрезка.Скачать

Онлайн калькулятор. Длина отрезка. Расстояние между точками.

Предлагаю вам воспользоваться онлайн калькулятором для вычисления расстояния между точками.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление расстояния между точками и закрепить пройденный материал.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Калькулятор для вычисления расстояния между двумя точками

Выберите необходимую вам размерность:

Введите координаты точек.

Ввод данных в калькулятор для вычисления расстояния между точками

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления расстояния между точками

Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.

Теория. Расстояние между точками.

Расстояние между двумя точками — это длина отрезка, что соединяет эти точки.

В зависимости от размерности задачи расстояние между двумя точками можно найти используя следующие формулы:

Формула вычисления расстояния от точки A( x_a , y_a ) до точки B( x_b , y_b ) на плоскости:

Формула вычисления расстояния от точки A( x_a , y_a , z_a ) до точки B( x_b , y_b , z_b ) в пространстве:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Длина отрезкаСкачать

Расчет евклидова расстояния с помощью NumPy

В этом руководстве мы рассмотрим, как рассчитать евклидово расстояние между двумя точками в Python с помощью Numpy.

Что такое евклидово расстояние?

Евклидово расстояние — это фундаментальная метрика расстояния, относящаяся к системам в евклидовом пространстве.

Евклидово пространство — это классическое геометрическое пространство, с которым вы знакомитесь на уроке математики, обычно связанное с 3 измерениями. Хотя его также можно приписать к любой неотрицательной целочисленной размерности.

Евклидово расстояние — кратчайшая прямая между двумя точками в евклидовом пространстве.

Название происходит от Евклида, который широко известен как «отец геометрии», так как это было единственное пространство, которое люди в то время обычно задумывали. Со временем в физике и математике наблюдались различные типы пространства, такие как пространство Аффин.

В 3-мерном евклидовом пространстве кратчайшая прямая между двумя точками всегда будет прямой линией между ними.

Учитывая этот факт, евклидово расстояние не всегда является наиболее полезной метрикой для отслеживания при работе со многими размерностями, мы сосредоточимся на 2D и 3D евклидовом пространстве для расчета евклидова расстояния.

Вообще говоря, евклидова расстояние широко используется в разработке 3D-миров, а также алгоритмов машинного обучения, которые включают в себя метрики расстояния, такие как K-ближайшие соседи. Как правило, евклидово расстояние будет представлять, насколько похожи две точки данных, предполагая, что некоторая кластеризация на основе других данных уже была выполнена.

Математическая формула

Математическая формула расчета евклидова расстояния между 2 точками в 2D пространстве:

Формула легко адаптируется к 3D-пространство, а также к любому размеру:

Общая формула может быть упрощена до:

Острый глаз может заметить сходство между евклидовым расстоянием и теоремой Пифагора:

На самом деле существует связь между ними — евклидовое расстояние рассчитывается с помощью теоремы Пифагора, учитывая декартовы координаты двух точек.

Из-за этого евклидова расстояние иногда называют расстоянием Пифагора, хотя прежнее название гораздо более известно.

Примечание: Две точки являются векторами, но выход должен быть скалярным.

Мы будем использовать NumPy для расчета этого расстояния для двух точек, и один и тот же подход используется для 2D и 3D пространств:

Расчет евклидова расстояния в Python с помощью NumPy

Во-первых, нам нужно будет установить библиотеку NumPy:

Теперь давайте импортируем его и настроим две наши точки с декартовыми координатами (0, 0, 0) и (3, 3, 3):

Вместо того, чтобы выполнять расчет вручную, мы будем использовать вспомогательные методы NumPy, чтобы сделать его еще проще!

Операции и математические функции, необходимые для расчета евклидова расстояния, довольно просты: сложение, вычитание, а также функция квадратного корня. Несколько слагаемых также можно заменить суммой:

NumPy предоставляет нам функцию np.sqrt(), представляющую функцию квадратного корня, а также функцию np.sum(), которая представляет собой сумму. При этом расчет евклидова расстояния в Python прост и интуитивно понятен:

Данная формула дает нам довольно простой результат:

Что равно 27. Осталось все, что получить квадратный корень из этого числа:

В истинном питоновом духе это можно сократить до одной строки:

И вы даже можете вместо этого использовать встроенные методы pow() и sum() математического модуля Python, хотя они требуют, чтобы вы немного поработали с вводом, который удобно абстрагируется с помощью NumPy, так как функция pow() работает только со скалярами (каждый элемент в массиве индивидуально) и принимает аргумент — в какой степени вы увеличиваете число.

Этот подход, однако, интуитивно больше похож на формулу, которую мы использовали раньше:

Это также приводит к:

np.linalg.norm()

Функция np.linalg.norm() представляет математическую норму. По сути, нормой вектора является его длина. Эта длина не обязательно должна быть евклидовым расстоянием, а может быть и другими расстояниями. Евклидово расстояние-это норма L2 вектора (иногда известная как евклидова норма), и по умолчанию функция norm() использует L2 — параметр ord имеет значение 2.

Если бы вы установили для параметра ord какое-то другое значение p, вы бы рассчитали другие p-нормы. Например, норма L1 вектора-это расстояние Манхэттена!

Имея это в виду, мы можем использовать функцию np.linalg.norm() для легкого и гораздо более чистого вычисления евклидова расстояния, чем использование других функций:

Это приводит к печати расстояния L2/евклида:

Нормализация L2 и нормализация L1 широко используются в машинном обучении для нормализации входных данных.

Мы также можем использовать точечное произведение для расчета евклидова расстояния. В математике точечное произведение является результатом умножения двух векторов равной длины, а результатом является единственное число — скалярное значение. Из-за возвращаемого типа его иногда также называют «скалярным продуктом». Эту операцию часто называют внутренним произведением для двух векторов.

Для расчета точечного произведения между 2 векторами вы можете использовать следующую формулу:

С помощью NumPy мы можем использовать функцию np.dot(), передавая два вектора.

Если мы вычислим точечное произведение разницы между обеими точками с той же разницей — мы получим число, которое находится в зависимости от евклидова расстояния между этими двумя векторами. Извлечение квадратного корня из этого числа дает нам расстояние, которое мы ищем:

Конечно, вы также можете сократить это до однострочного:

Использование встроенной системы math.dist()

В Python есть встроенный метод в математическом модуле, который вычисляет расстояние между 2 точками в трехмерном пространстве. Однако это работает только с Python 3.8 или более поздней версии.

math.dist()принимает два параметра, которые являются двумя точками, и возвращает евклидово расстояние между этими точками.

Примечание: Обратите внимание, что две точки должны иметь одинаковые размеры (т.е. оба в 2d или 3d пространстве).

Теперь, чтобы вычислить Евклидово расстояние между этими двумя точками, мы просто заправляем их в метод thedistdist():

Заключение

Данная метрика используется во многих контекстах в интеллектуальном анализе данных, машинном обучении и ряде других областей и является одной из фундаментальных метрик расстояния.