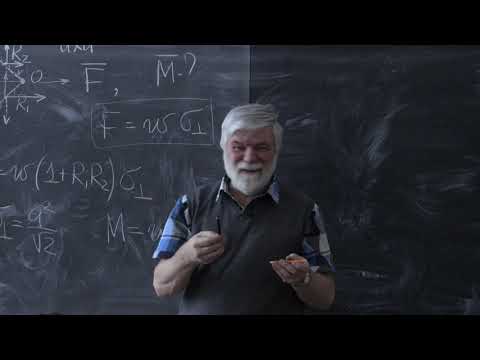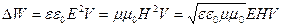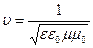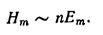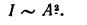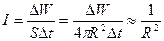Интенсивность и световой вектор (6 видео)

Интенсивность света, связь интенсивности света с амплитудой светового вектора.

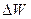
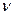
Интенсивностью света называют электромагнитную энергию , проходящую в единицу времени через единицу площади поверхности, перпендикулярной направлению распространения света. Частоты видимых световых волн лежат в пределах

= (,39 4-0,75)-10 15 Гц.

Ни глаз, ни какой-либо иной приемник световой энергии не может уследить за столь частыми изменениями потока энергии, вследствие чего они регистрируют усредненный по времени поток. Поэтому правильнее определить интенсивность как модуль среднего по времени значения плотности потока энергии, переносимой световой волной. Плотность потока электромагнитной энергии определяется выражением

(4.4)

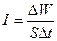
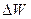
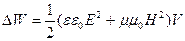
Поскольку световая волна- это электромагнитная волна, то складывается из энергии магнитного и электрического полей

(4.5)

где V- объем, занимаемый волновым полем.

Из уравнений Максвелла следует, что векторы напряженности электрического и магнитного полей в электромагнитной волне связаны соотношением

(4.6)

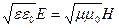
Поэтому выражение (4.5) можно записать следующим образом

Из уравнений Максвелла скорость распространения электромагнитных волн

Выделим некоторый объем волнового поля в форме параллелепипеда (рис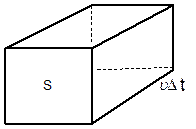.4.5)

Рис.4.5

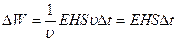
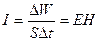
Тогда , по определению интенсивности

, используя выражение (4,6) и полагая, что в прозрачной среде m=1 получим

где n— показатель преломления среды, в которой распространяется волна. Таким образом, напряженность магнитного поля Н пропорционально напряженности электрического поля Е и n:

Тогда интенсивность волны будет определяться выражением

(4.7)

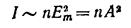
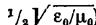
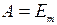
(коэффициент пропорциональности равен )- Следовательно, интенсивность света пропорциональна показателю преломления среды и квадрату амплитуды вектора напряженности электрического поля световой волны. Заметим, что при рассмотрении распространения света в однородной среде можно считать, что интенсивность пропорциональна квадрату амплитуды вектора напряженности электрического поля ( ) световой волны:

Однако в случае прохождения света через границу раздела сред выражение для интенсивности, не учитывающее множитель n, приводит к не сохранению светового потока.

Рассмотрим сферическую световую волну. Площадь сферического фронта волны 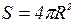, где R- радиус фронта волны. Согласно уравнению (4,4) находим интенсивность

Эти выражения показывают, что амплитуда сферической волны уменьшается пропорционально расстоянию от источника световых волн. Если R достаточно велико, т.е. источник находится очень далеко от области наблюдения, то фронт волны представляется частью сферической поверхности очень большого радиуса. Ее можно считать плоскостью. Волна, фронт волны которой представляется плоскостью, называется плоской, так как энергия волны во всех плоскостях, представляющих фронты волны в различные моменты времени остается постоянной, то амплитуда у такой волны постоянна.

.Понятие интерференции, наложение гармонических волн, условия когерентности.

Свет является электромагнитной волной. Сложение волн, распространяющихся в среде, определяется сложением соответствующих колебаний. Рассмотрим наиболее простой случай сложения электромагнитных волн (колебаний):

1) частоты их одинаковы,

2) направления электрических векторов совпадают.

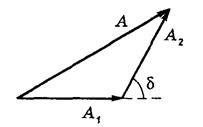
В этом случае для каждой точки среды, в которой происходит сложение волн, амплитуда результирующей волны для напряженности электрического поля определяется векторной диаграммой (рис.4.6)

Из диаграммы следует, что результирующая амплитуда определится следующим образом:

(4.8)

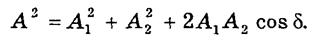
где d— разность фаз слагаемых волн (колебаний).

Результат сложения волн зависит от особенностей источников света и может быть различен.

Дата добавления: 2017-10-04 ; просмотров: 24919 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Содержание

Интенсивность и давление света
Давление света
Примеры
Интенсивность и давление света
Интенсивность света
Готовые работы на аналогичную тему
Давление света
🔍 Видео

Видео:Поляризация света и закон МалюсаСкачать

Интенсивность и давление света

Интенсивность света I в выбранной точке – это модуль средней по времени величины плотности потока энергии, которую световая волна переносит.

Определение плотности потока электромагнитной энергии возможно при помощи вектора Умова-Пойнтинга P → . Отсюда следует, что математический вид определения интенсивности света записывается в виде формулы:

I = » open=» P → = » open=» E → × H → .

По выражению усреднение проводится за период времени t , причем больший по сравнению с периодом колебания волны T t ≫ T . Интенсивность света записывается как:

I t = 1 T ∫ t t + T P → ( t ) d t .

В системе С И единицей измерения является В т м 2 .

Модули амплитуд ( E m и H m ) векторов напряженностей электрического E → и магнитного H → полей в электромагнитной волн записываются в виде отношения:

Имеем, что μ ≈ 1 . Необходимо выразить амплитуду H m :

где n = ε μ = ε при μ ≈ 1 является показателем преломления вещества, в котором распространяется свет.

Модуль среднего значения вектора Умова-Пойнтинга пропорционален произведению амплитуд E m · H m .

Интенсивность света не может быть измерена в связи с тем, что поле изменяется с высокой частотой ν = 10 15 Г ц , соответственно период колебаний составляет T = 10 — 15 с , а приемники колебаний обладают временем инерции существенно больше, чем 10 — 15 c .

Отсюда следует, что среднее значение интенсивности можно регистрировать. Также возможно измерение средней интенсивности, но не фазы поля.

Видео:Урок 374. Энергия, переносимая волной. Интенсивность сферической волныСкачать

Давление света

По закону сохранения при поглощении и отражении света телом ему сообщается импульс, равняющийся разности импульсов пучка света до и после этих процессов. Отсюда следует, что на тело действует сила, свет производит соответствующее давление на тело. Еще Кеплер выдвинул свое предположение о существовании давления света, которое было принято при рассмотрении отклонений хвостов комет от Солнца.

Последователи волновой теории отрицали давление света, отсутствие доказательств опытами о существовании светового давления служило аргументом против корпускулярной. То есть существование светового давления считалось следствием электромагнитной теории.

Если световая волна падает перпендикулярно плоскости поверхности тела и полностью поглощает свет, то определение давления p производится по формуле.

Где G считается плотностью импульса световой волны, P – модулем вектора Умова-Пойнтинга, с – скоростью света в вакууме.

Если происходит полное отражение света при помощи поверхности тела, то импульс, который при помощи него передается, имеет значение в 2 раза больше, также как и значение давления.

При падении световой волны на поверхность под углом относительно нормали, производя расчеты давления, применяют только перпендикулярную составляющую плотности потока энергии. Если имеются обычные условия, то давление крайне малое, то есть в 10 10 раз меньше атмосферного.

П.Н. Лебедев в 1899 году смог измерить световое давление. Для этого он применил крутильные весы, находящиеся в вакууме. Позже его опыты определения существования давления света подтвердили электромагнитную теорию света Максвелла.

Давление электромагнитных волн считается результатом воздействия электрического поля волны частицы вещества, которые обладают электрическим зарядом, движутся упорядоченно, на них действуют силы Лоренца.

Видео:Физика 11 класс (Урок№16 - Интерференция света.)Скачать

Примеры

Определить давление, оказываемое плоской световой волной, падающей перпендикулярно относительно поверхности тела и поглощаемой телом. Значение амплитуды напряженности электрического поля равняется 2 В м .

Будем использовать формулу:

p = » open=» P c ( 1 . 1 ) .

Где » open=» P принимается за среднее значение модуля вектора Умова-Пойнтинга, c = 3 · 10 8 м с – за скорость света в вакууме.

Для нахождения среднего значения модуля вектора Умова-Пойнтинга необходимо использовать:

» open=» P = » open=» E · H ( 1 . 2 ) .

В условии имеем плоскую волну, тогда уравнение ее колебаний зафиксируем как:

E = E m cos ω t — k x , H = H m cos ω t — k x ( 1 . 3 ) .

Для нахождения значения амплитуды напряжения магнитного поля следует применить:

ε ε 0 E m = μ μ 0 H m ( 1 . 4 ) .

Когда для вакуума ε = 1 , μ = 1 , можно выразить из ( 1 . 4 ) H m . Получим:

H m = ε 0 μ 0 E m ( 1 . 5 ) ,

где μ 0 = 4 π · 10 — 7 Г н м , ε 0 = 1 4 π · 9 · 10 9 Ф м . Это говорит о том, что средним значением модуля вектора Умова-Пойнтинга будет:

» open=» P = » open=» E m cos ω t — k x · ε 0 μ 0 E m cos ω t — k x = ε 0 μ 0 E m 2 » open=» cos ω t — k x = = 1 2 ε 0 μ 0 E m 2 ( 1 . 6 ) .

Далее производим подстановку правой части выражения ( 1 . 6 ) в ( 1 . 1 ) вместо » open=» P , тогда искомое давление света:

p = 1 2 ε 0 μ 0 E m 2 c .

Заменим числовые значения и получим:

p = 1 2 · 3 · 10 8 1 4 π · 10 — 7 · 4 π · 9 · 10 9 · 4 = 4 120 π · 6 · 10 8 = 1 , 77 · 10 11 ( П а )

Ответ: 17 , 7 п П а .

Определить интенсивность I плоской световой волны, распространяющейся вдоль О х . Значение напряженности электрического поля волны равняется E m В м .

Из определения выявим интенсивность световой волны:

I = » open=» P ( 2 . 1 ) .

Запись модуля вектора Умова-Пойтинга для плоской световой волны обозначится как:

P = E H = E m H m cos 2 ω t — k x ( 2 . 2 ) .

Среднее значение » open=» P :

» open=» P = 1 2 E m H m 2 . 3 , так как » open=» cos 2 ω t — k x = 1 2 .

Сравнивая с примером 1 , можно произвести выражение амплитуды напряженности магнитного поля:

ε ε 0 E m = μ μ 0 H m → H m = ε ε 0 μ μ 0 E m ( 2 . 4 ) .

Из ( 2 . 1 ) , ( 2 . 3 ) , ( 2 . 4 ) получим:

Видео:Урок 420. Дифракция света. Дифракционная решеткаСкачать

Интенсивность и давление света

Вы будете перенаправлены на Автор24

Видео:Оптические Зазеркалья. Лекция 1_5. Интенсивность и поляризацияСкачать

Интенсивность света

Интенсивностью света ($I$) в избранной точке называют модуль средней по времени величины плотности потока энергии, которую световая волна переносит. В свою очередь плотность потока электромагнитной энергии определяют с помощью вектора Умова — Пойнтинга ($overrightarrow

$). Значит, в математическом виде определение интенсивности света можно записать как:

[I=left|leftlangle overrightarrow

rightrangle right|=left|leftlangle overrightarrowtimes overrightarrowrightrangle right|left(1right),]

где усреднение производят за время ($t$) много большее, чем период ($T$) колебаний волны: ($tgg T$). Определение интенсивности света можно записать в виде:

Единицами измерения интенсивности света в $СИ$, обычно служат $frac.$

Модули амплитуд ($E_m и H_m$) векторов напряжённостей электрического ($overrightarrow$) и магнитного ($overrightarrow$) полей в электромагнитной волне связаны соотношением:

где считаем, что $mu approx 1.$ Выразим из (3) амплитуду $H_m$, получим:

где $n=sqrt=sqrt$ при $mu approx 1$- показатель преломления вещества, в котором распространяется свет. Из выражения (4) следует, что:

Модуль среднего значения вектора Умова — Пойнтинга пропорционален произведению амплитуд $E_m cdot H_m$, значит можно записать, что интенсивность света:

Интенсивность света не может быть измеряна в связи с тем, что поле изменяется с высокой частотой ($nu =^Гц$), соответственно период колебаний составляет $T=^с$, тогда как приемники колебаний имеют время инерции существенно больше, чем $^с$. Следовательно, регистрировать мы можем среднее значение интенсивности. Кроме того, можно измерять среднюю интенсивность, но не фазу поля.

Готовые работы на аналогичную тему

Видео:ФИЗИКА ЗА 5 МИНУТ - ОПТИКАСкачать

Давление света

В соответствии с законом сохранения в случае, когда тело поглощает или отражает свет, ему сообщается импульс, который равен разности импульсов пучка света до и после поглощения или отражения. Значит, на тело действует сила, свет производит на тело соответствующее давление. Предположение о существовании давления света была выдвинута Кеплером, который рассматривал отклонение хвостов комет от Солнца.

Сторонниками волновой теории давление света отрицалось, отсутствие эмпирических доказательств существования светового давления считалось аргументом против корпускулярной теории света. Существование светового давления является следствием электромагнитной теории.

При перпендикулярном падении световой волны на плоскую поверхность тела, и полном поглощении света, его давление ($p$) определяют как:

где $G$ — плотность импульса световой волны, $P$ — модуль вектора Умова — Пойнтинга (надо отметить, что на практике часто используют его среднее значение), $c$ — скорость света в вакууме.

В случае полного отражения света поверхностью тела импульс, передаваемый светом в два раза больше, соответственно больше во столько же давление.

Если энергия световой волны поглощается телом частично, при этом плотность потока поглощаемой энергии ($P_$) вычисляется как:

при этом плотность потока отражаемой энергии ($P_$) выразим как:

Принимая во внимание выражения (8) и (9) давление определим:

Если световая волна падает на поверхность тела под углом к нормали, то при расчете давления используют только перпендикулярную составляющую плотности потока энергии. Давление света при обычных условиях кране мало, примерно в $^ $меньше атмосферного.

Первым световое давление измерил П.Н. Лебедев в 1899 г. Он использовал для этого крутильные весы, которые находились в вакууме. Значение опытов Лебедева в том, что существование давления света подтверждало электромагнитную теорию света Максвелла.

Итак, давление электромагнитных волн — результат того, что при воздействии электрического поля волны частицы вещества, обладающие электрическим зарядом, упорядочено движутся, на них действуют силы Лоренца.

Задание: Каким будет давление, которое оказывает плоская световая волна, которая падает перпендикулярно на поверхность тела и полностью телом поглощается? Амплитуда напряженности электрического поля при этом равна $2frac$.

Решение:

За основу решения задачи примем выражение:

где $leftlangle Prightrangle $ — среднее значение модуля вектора Умова — Пойнтинга, $c=3cdot ^8frac$ — скорость света в вакууме.

При этом среднее значение модуля вектора Умова — Пойнтинга найдем как:

[leftlangle Prightrangle =leftlangle Ecdot Hrightrangle left(1.2right).]

Так как по условию задачи мы имеем плоскую волну, то уравнение колебаний ее составляющих запишем как:

Для того чтобы найти значение амплитуды напряжения магнитного поля воспользуемся соотношением:

Используем то, что для вакуума $varepsilon $=1, $mu =1$, выразим из (1.4) $H_m$, имеем:

где $mu_0=4pi cdot ^frac, varepsilon_0=frac<4pi cdot ^9>frac$. В таком случае среднее значение модуля вектора Умова — Пойнтинга равно:

Подставим правую часть выражения (1.6) в формулу (1.1) вместо величины $leftlangle Prightrangle $, получим искомое давление света:

Ответ: $p=17,7пПа.$

Задание: Какой будет интенсивность ($I$), плоской световой волны, которая распространяется вдоль $оси X$? Амплитуда напряженности электрического поля волны при этом равна $E_m(frac)$.

Решение:

По определению интенсивность световой волны можно найти как:

[I=leftlangle Prightrangle left(2.1right).]

Для плоской световой волны модуль вектора Умова — Пойнтинга запишем как (см. Пример 1):

Тогда среднее значение $leftlangle Prightrangle $ можно выразить как:

[leftlangle Prightrangle =fracE_mH_mleft(2.3right),]

так как $leftlangle c^2left(omega t-kxright)rightrangle =frac.$

При этом так же, как в примере 1, выразим амплитуду напряженности магнитного поля:

Используя выражения (2.1), (2.3) и (2.4), запишем:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 26 02 2022