Как начертить окружность пунктиром (2 видео)

Окружность. Круг. Приемы работы циркулем, использование трафаретов

Цели и задачи:

Дать определение окружность, круг.
Научить делить окружность на равные части.
Научить выполнять геометрические построения при помощи циркуля и трафаретов.
Ознакомить с применением данных геометрических построений в различных областях деятельности человека.
Воспитывать терпение, аккуратность при выполнении заданий.

Тип урока: комбинированный.

Формы работы: индивидуальная, групповая.

Содержание

Ход занятия:
Организационный момент:
Повторение:
Новый материал:
Физкультурная пауза.
Закрепление:
Запомни:В центре должны обязательно пересекаться штрихи, проведенных центровых (осевых) линий, а не точки.В окружностях меньших размеров допускается проводить вместо штрихпунктирных линий тонкие линии построения.
Круг. Окружность (центр, радиус, диаметр)
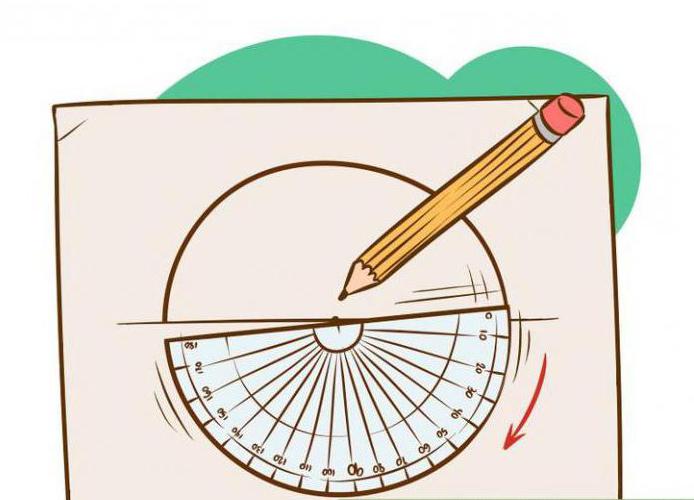
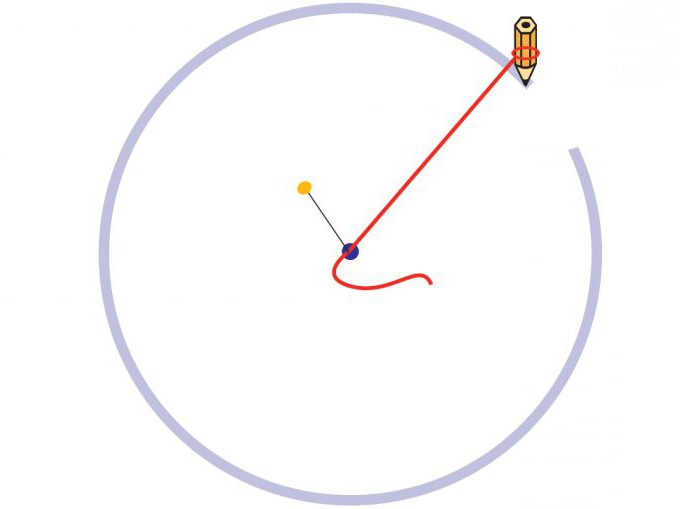
Как правильно чертить циркулем
Очень простой способ получения круглого элемента – вместо циркуля используем скрепку
Как нарисовать ровный круг без помощи циркуля
Рисуем круги разного размера без вспомогательных предметов
Как нарисовать идеальную окружность при помощи линейки
Popular
Основы черчения
Строительное
Машиностроительное
📸 Видео

Видео:Школа для родителей. Циркуль, окружность, радиус, диаметр.Скачать

Ход занятия:

Организационный момент:

Проверка готовности к уроку.

Повторение:

Анализ графического упражнения.

Новый материал:

Рубрика «Это интересно!»

С незапамятных времен человек использовал в своей жизни простейшие геометрические построения. Одним из таких построений является деление окружности на равные части. Примеров можно привести много. Превращение колеса из сплошного диска в обод со спицами поставило человека перед необходимостью распределить спицы в колесе равномерно.

С делением окружности неразрывно связано построение правильных многоугольников. Правильные многоугольники встречаются в древнейших орнаментах у всех народов.

В декоративно- прикладном искусстве дизайнеры, ювелиры и представители многих других профессий с успехом применяли деление окружности, создавая прекрасные произведения. Это ордена, медали, монеты и ювелирные украшения.

Орден Красной Звезды
Орден Отечественной войны

Самым распространенным примером применение деления окружности на равные части является создание логотипов, эмблем, товарных знаков различных фирм. Иногда достаточно увидеть эмблему на капоте или крыле автомобиля и безошибочно назвать марку.

Показ наглядных пособий использования геометрических построений в строительстве, архитектуре, машиностроении, а также природные явления.

Построение круга, окружности.

Круг – это часть плоскости, ограниченная окружностью.

Окружность – замкнутая плоская кривая, все точки которой равноудалены от центра.

Чтобы изобразить круг, достаточно взять блюдце или тарелку и обвести.

Для построения окружности необходимо найти центр. Из центра циркулем провести окружность.

Этапы построения:

Начертить квадрат.
Разделить стороны квадрата на две равные части, отметить буквами или цифрами.
Через полученные точки провести центровую линию (штрихпунктирную) Сначала горизонтальную, затем вертикальную.
Пересечение линий отметить точкой О – центр окружности.
В точку О поставить ножку циркуля и начертить окружность. Центр окружности является также и центром круга.

Запомнить: в центре должны обязательно пересекаться штрихи, проведенных центровых (осевых) линий, а не точки. В окружностях меньших размеров допускается проводить вместо штрихпунктирных линий тонкие линии построения.

Для построения окружностей и кругов используют трафареты.

Демонстрация, показ.

Деление окружности на равные части.

Любая прямая, проведенная через центр окружности, делит эту окружность на две равные части. Две взаимно перпендикулярные прямые, проведенные через центр окружности, делят эту окружность на 4 равные части.

Окружность можно разделить на 8 равных частей, используя линейку или угольники.

Демонстрация, показ.

Если соединить, полученные при делении точки окружности, то мы получим правильные многоугольники.

При делении окружности на 3, 6, 12 равных частей используют не только угольники, но и циркуль. В результате построения можно увидеть правильный равносторонний треугольник, правильный шестиугольник (рисунок 5)

Демонстрация, показ.

Физкультурная пауза.

Закрепление:

Фрагмент из рабочей тетради.

Приготовь для работы циркуль, карандаш с маркировкой Т и ТМ, линейку, трафарет. Все построения выполняй аккуратно.

Используя трафарет с окружностями, изобрази круг.

Для построения окружности необходимо провести штрихпунктирные линии. Эти линии состоят из штриха и точки. При пересечении они образуют центр окружности и являются центровыми или осевыми линиями.

Установи ножку циркуля в центре пересечения осевых (центровых) линий и проведи окружность.

Этапы построения окружности:

Начертить квадрат.
Разделить все стороны квадрата на две равные части, отметить полученные точки.
Через точки провести центровую линию (штрихпунктирную) карандашом с маркировкой Т. Сначала горизонтальную, затем вертикальную.
Пересечение линий отметить точкой О – центр окружности.
В точку О поставить ножку циркуля и начертить окружность.

Центр окружности является также и центром круга.

Запомни:
В центре должны обязательно пересекаться штрихи, проведенных центровых (осевых) линий, а не точки.
В окружностях меньших размеров допускается проводить вместо штрихпунктирных линий тонкие линии построения.

Рубрика «ЗАПОМНИ»: круг, окружность, осевая линия, центровая линия, штрихпкнктирная линия.

Видео:Типы линий. Урок1.(Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Круг. Окружность (центр, радиус, диаметр)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Данный урок посвящён изучению окружности и круга. Также учитель научит отличать замкнутые и незамкнутые линии. Вы познакомитесь с основными свойствами окружности: центром, радиусом и диаметром. Выучите их определения. Научитесь определять радиус, если известен диаметр, и наоборот.

Видео:ПРИЕМЫ РАБОТЫ С ЧЕРТЕЖНЫМ ИНСТРУМЕНТОМ. Линии чертежа. Видео для начинающихСкачать

Как правильно чертить циркулем

Очень простой способ получения круглого элемента – вместо циркуля используем скрепку

Одна, две или три скрепки, соединенные между собой, помогут нам нарисовать три круга с разными радиусами. Проект полезен для детей, если они хотят быстро начертить круг с диаметрами около 4, 9 и 15 см (диаметр зависит от типа и размеров скрепок). Высокой точности вы не добьетесь, но форма будет соблюдена. Хороший опыт для любителей нестандартного подхода. Работа с одновременным взаимодействием нескольких фломастеров (карандашей) и скрепок развивает ловкость детских рук.

Материалы:

Ход работы:

Проще, конечно, нарисовать круг, обведя круглый предмет – чашку, тарелку, монету и т. п. Но есть еще и такой нестандартный способ, о котором стоит узнать школьникам.

Итак, положите в центр листа скрепку. Возьмите фломастер и поставьте его вертикально на бумагу. Стержень должен прикасаться к краю скрепки, а другой фломастер вставляется с другой стороны скрепки. Один фломастер вы будете держать неподвижно, а другой проворачивать вместе со скрепкой, не меняя радиус круга. Вы можете двигаться по кругу в ту сторону, куда вам удобно.

Теперь сделаем круг немного шире. Для этого вам надо соъединить две или три скрепки, удобно уложить на плоскость, а затем повторить движение по часовой стрелке или против.

Если вы хотите, чтобы центр круга был незаметным, используйте заточенный простой карандаш или инструмент для квиллинга, как в проекте.

Рисование окружностей различного диаметра – далеко не самый нужный навык в жизни. Однако рано или поздно необходимость нарисовать круг без циркуля и других вспомогательных предметов круглой формы застает всех врасплох. Поэтому лучше заранее узнать о том, как нарисовать круг без циркуля вне зависимости от его диаметра.

Видео:Как нарисовать идеально ровный круг без циркуля Круг для наждакаСкачать

Как нарисовать ровный круг без помощи циркуля

Вы можете быть школьником, который пришел на урок геометрии, забыв инструменты для черчения, студентом, взрослым человеком, вынужденным начертить идеально ровную окружность, – ситуации случаются разные.

Каждому человеку полезно будет знать, как нарисовать ровный круг без циркуля. Мы предлагаем вам несколько способов решения данной задачи.

Заменить циркуль легко может другой инструмент, находящийся в пенале у каждого школьника, а именно – транспортир. Положите его на бумагу, отметив центральную точку на прямой части, это будет центр будущего круга. Обведите внутреннюю часть полукруга, затем поверните линейку примерно на девяносто градусов и дорисуйте треть круга. Поверните транспортир еще раз и завершите круг.

Если вы находитесь на совещании или на рабочем месте, но под рукой не оказалось нужного инструмента, просто воспользуйтесь компакт-диском. Обведите его с внешней стороны или с внутренней для получения фигуры меньшего размера.

В офисной обстановке можно также воспользоваться стаканом. Для этого возьмите стакан с водой, сделайте глоток и поставьте на лист бумаги, легким движением обведите дно. Попейте еще и отставьте его в сторону.

Все вышеперечисленные предметы можно найти в любом офисе, транспортир будет доступен и ученикам. С помощью них вы сможете ровно нарисовать круг без циркуля.

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Рисуем круги разного размера без вспомогательных предметов

Что же делать, если требуется нарисовать окружности разного диаметра?

Совсем не сложно справиться с этой проблемой, имея под рукой лишь бумагу и простой карандаш.

Возьмите карандаш в одну руку, вторую положите на лист бумаги. Мизинец первой руки расположите на листе так, чтобы он был центром будущего круга. Хорошо зафиксируйте это положение. Второй рукой начинайте поворачивать бумагу вокруг мизинца. Вы увидите, как получается ровная окружность, как при использовании циркуля.

Круг большего размера рисуется так же, но в этом случае мизинец согните, как если бы сжали все пальцы в кулак. Левой рукой начинайте поворачивать лист, пока не увидите получившийся круг. Желательно использовать карандаш с мягким грифелем.

Круг с еще большим диаметром можно нарисовать, повторив все вышеуказанные советы, но теперь правая рука должна касаться листа выступающей косточкой на запястье.

Это самые простые методы того, как нарисовать круг без циркуля. Самое главное в этих способах – научиться держать правую руку неподвижной (левую, если вы левша).

Видео:Радиус и диаметрСкачать

Как нарисовать идеальную окружность при помощи линейки

Если под рукой у вас найдется обычная линейка, то вы можете воспользоваться еще одним советом, как нарисовать круг без циркуля. Возьмите линейку и приложите ее к бумаге, отметка ”0” будет центром круга, поэтому поставьте ее в нужном месте. Вторую точку нарисуйте возле цифрового значения, соответствующего радиусу круга. Немного сместите второй край линейки так, чтобы середина оставалась на нуле, а третья точка располагалась чуть выше второй.

Проделайте эту процедуру несколько раз. В результате у вас должна получиться окружность, нарисованная пунктирной линией. Чем чаще пунктир, тем легче будет соединить все в сплошную линию.

Это, пожалуй, самый легкий, но вместе с тем и самый долгий способ того, как нарисовать круг без циркуля.

Основы черчения

Строительное

Машиностроительное

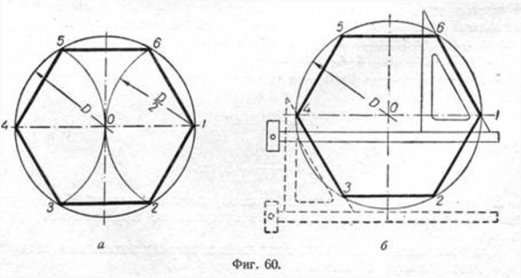
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.

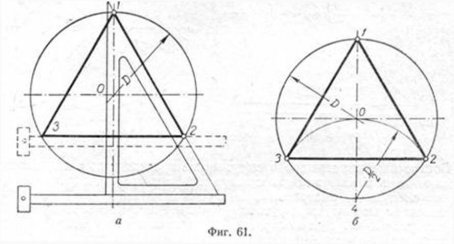
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.

Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны

1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.

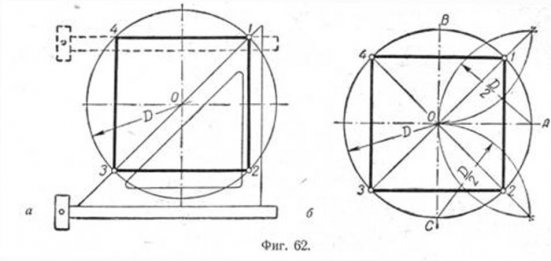
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

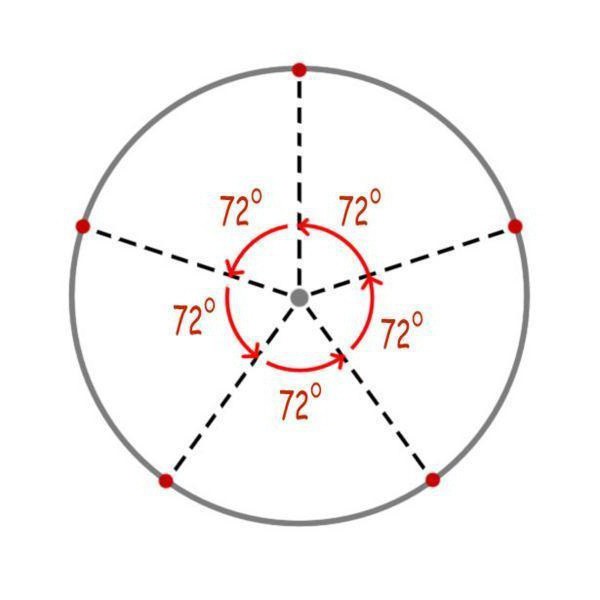
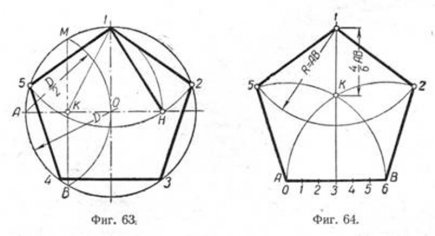
Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.

Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.

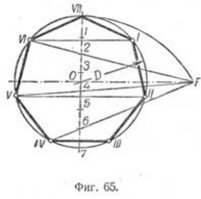
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.

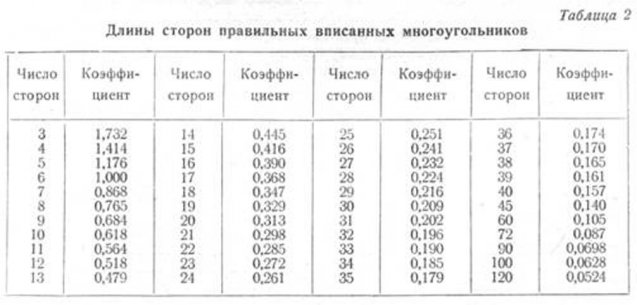
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.

Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.