Выберите верные утверждения прямая не лежащая в данной плоскости и параллельная какой

Геометрия. 10 класс. Глава I. Тест 1.

Вариант 1.

1. Выбрать верное утверждение.

1) Две прямые в пространстве называются параллельными, если они не пересекаются.

2) Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо тоже параллельна данной плоскости, либо лежит в этой плоскости.

3) Если прямая параллельна какой-нибудь прямой, лежащей в плоскости, то она параллельна этой плоскости.

4) Через любую точку пространства проходит прямая, параллельная данной прямой, и притом только одна.

A) 1; B) 4; C) 3; D) 2.

2. Какой из чертежей на рисунке 1 может служить иллюстрацией следующего утверждения: если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость?

A) б); B) а); C) в); D) г).

3. На рисунке 2 точки E, F, P и K –середины отрезков АС, АМ, ВМ и ВС. Найти периметр четырёхугольника EFPK,

если МС=21 см, АВ=13 см.

A) 8 см; B) 34 см; C) 17 см; D) 68 см.

4. Сторона АС треугольника АВС лежит в плоскости α. МϵАВ, NϵBC, MN||α, причём BM:AM=2:7, MN=6 см. Сделать чертёж. Найти АС.

A) 18 см; B) 30 см; C) 27 см; D) 36 см.

Вариант 2.

1. Выбрать верное утверждение.

1) Если плоскость проходит через прямую, параллельную другой плоскости, то эти плоскости будут параллельны.

2) Если две прямые параллельны третьей прямой, то они перпендикулярны.

3) Если прямая параллельна какой-нибудь прямой, лежащей в плоскости, то она параллельна данной плоскости.

4) Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

A) 1; B) 4; C) 3; D) 2.

2. Какой из чертежей на рисунке 1 может служить иллюстрацией следующего утверждения: через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна?

A) б); B) а); C) в); D) г).

3. На рисунке 2 точки F, P, Q и N –середины отрезков АB, АМ, CМ и ВС. Найти периметр четырёхугольника FPQN, если AС=17 см, ВM=25 см.

A) 32 см; B) 21 см; C) 42 см; D) 84 см.

4. Плоскость α параллельна стороне АС треугольника АВС и пересекает стороны АВ и ВС в точках К и F соответственно, BF:FC=5:6, АС=22 см. Сделать чертёж. Найти KF.

A) 15 см; B) 9 см; C) 10 см; D) 12 см.

Вариант 3.

1. Выбрать верные утверждения.

1) Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

2) Если параллельные прямые а и b лежат в плоскости α, то и прямая с, пересекающая прямые а и b, лежит в плоскости α.

3) Если средняя линия трапеции лежит в плоскости α, то прямые, содержащие её основания пересекут плоскость α.

A) 1); 2); 3); B) 1); 3); C) 1); 2); D) 2); 3).

2. Каким чертежом (какими чертежами) на рисунке 1 можно проиллюстрировать следующее утверждение.

Возможны три случая взаимного расположения прямой и плоскости: а) прямая и плоскость имеют только одну общую точку; б) прямая лежит в плоскости; в) прямая и плоскость не имеют ни одной общей точки.

А) б); в); B) а); б); г); C) б); в); г); D) а).

3. На рисунке 2 точки E, F, P и K – середины отрезков АС, АМ, ВМ и ВС. Периметр четырёхугольника EFPK равен 32 см, причём разность длин любых его смежных сторон составляет 2 см. Найти МС и АВ (МС

A) MC=14 см; AB=18 см; B) MC=15 см; AB=17 см;

C) MC=12 см; AB=20 см; D) MC=10 см; AB=22 см.

4. Отрезок АВ пересекает плоскость α в точке О. Точка С – середина отрезка ОВ. Параллельные прямые, проведённые из точек А, В и С к плоскости α, пересекают её в точках А₁, В₁ и С₁ соответственно. АА₁=6 см, А₁О:ОС₁=1:3. Сделать чертёж. Найти ВВ₁.

A) 18 см; B) 30 см; C) 32 см; D) 36 см.

Вариант 4.

1. Выбрать верные утверждения.

1) Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

2) Возможны три случая взаимного расположения прямой и плоскости: а) прямая лежит в плоскости; б) прямая и плоскость пересекаются; в) прямая и плоскость параллельны.

3) Если стороны MN и NP параллелограмма MNPQ пересекают плоскость α, то и прямые MQ и PQ пересекут эту плоскость.

A) 1); 2); 3); B) 1); 3); C) 1); 2); D) 2); 3).

2. Каким чертежом (какими чертежами) на рисунке 1 можно проиллюстрировать следующее утверждение.

Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

А) б); в); B) а); C) а); б); D) а); г).

3. На рисунке 2 точки F, P, Q и N – середины отрезков АB, АМ, CМ и ВС. Периметр четырёхугольника FPQN равен 38 см, причём разность длин любых его смежных сторон составляет 3 см. Найти AС и BM (AС

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Выберите верные утверждения прямая не лежащая в данной плоскости и параллельная какой

Тесты по геометрии 10 класс. Тема: «Параллельность прямых и плоскостей»

Правильный вариант ответа отмечен знаком +

1. Какими называют плоскость и прямую, не имеющих ни одной общей точки?

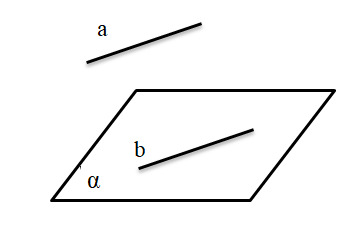
2. Посмотрите на рисунок и выберите правильное утверждение:

— Прямая а и плоскость α являются перпендикулярными.

— В плоскости α находится прямая а.

— Плоскость α и прямая b являются перпендикулярными.

+ Плоскость α и прямая а являются параллельными друг другу.

3. Сколько случаев взаимного расположения прямой и плоскости в пространстве имеется?

4. В каком варианте ответа указано правильное суждение?

— Не находящаяся в данной плоскости прямая считается параллельной этой плоскости, если она пересекается с какой-либо прямой, находящейся на этой плоскости.

+ Если прямая не принадлежит данной плоскости и является параллельной какой-либо прямой на этой плоскости, то она считается параллельной данной плоскости.

— Не находящаяся в данной плоскости прямая, которая является параллельной лежащей на этой плоскости прямой, считается перпендикулярной данной плоскости.

— Если прямая не принадлежит данной плоскости и является перпендикулярной какой-либо лежащей на этой плоскости прямой, то она считается параллельной данной плоскости.

5. Через сколько точек можно провести лишь одну плоскость?

— невозможно провести только одну плоскость

6.Если прямая K и плоскость α обладают одной общей точкой, то это значит, что:

— плоскость α и прямая K характеризуются параллельностью между собой.

+ плоскость α и прямая K пересекаются.

— прямая K находится в плоскости α.

— прямая K параллельна другой прямой, лежащей в плоскости α.

7. Плоскости S и T пересекаются третьей плоскостью U. Из этого следует, что:

— плоскости S и T перпендикулярны плоскости U.

— плоскости S и U являются параллельными.

— плоскости T и U являются параллельными.

+ линии пересечения плоскостей являются параллельными.

8. Выберите правильное утверждение:

+ При условии, что плоскость проходит через данную прямую, являющуюся параллельной другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей всегда параллельна данной прямой.

— Чтобы линия пересечения плоскостей была параллельна прямой, плоскость должна проходить через прямую, являющуюся перпендикулярной другой плоскости, и пересекать эту плоскость.

— Если линия пересечения плоскостей параллельна данной прямой, то плоскость проходит через эту прямую, являющуюся параллельной другой плоскости, и не пересекает эту плоскость.

— Чтобы линия пересечения плоскостей была перпендикулярна прямой, плоскость должна проходит через прямую, являющуюся параллельной другой плоскости, и пересекать эту плоскость.

9. Каких плоскостей называют параллельными?

тест 10. Даны две параллельные между собой прямые Y и Z. Одна из них, а именно прямая Z, параллельна данной плоскости. Значит, прямая Y:

— не принадлежит данной плоскости или является ей перпендикулярной.

— и данная плоскость являются скрещивающимися или она лежит в этой плоскости.

+ находится в данной плоскости или параллельна этой плоскости.

— параллельна данной плоскости или не лежит этой плоскости.

11. У плоскости α и прямой D множество общих точек. Это обозначает, что:

— плоскость α и прямая D являются перпендикулярными.

— плоскость α и прямая D пересекаются в одной точке.

— прямая D и плоскость α параллельны между собой.

+ прямая D находится в плоскости α.

12. В плоскости α лежит основа BC треугольника ABC. Точка P является серединой основы BC. Выберите правильное суждение:

— Прямые AP и BC являются параллельными.

— Прямая AP и плоскость α являются параллельными.

+ Прямая CP находится в плоскости α.

— Прямые AP и BC не пересекаются.

13. В каких случаях плоскостей можно считать параллельными?

+ При условии, что две находящиеся в одной плоскости пересекающиеся прямые параллельны двум лежащим в другой плоскости пересекающимся прямым.

— При условии, что две лежащие в разных плоскостях параллельные прямые перпендикулярны двум находящимся в другой плоскости параллельным прямым.

— При условии, что две пересекающиеся и находящиеся в одной плоскости прямые перпендикулярны двум лежащим в другой плоскости пересекающимся прямым.

— При условии, что одна находящаяся в одной плоскости прямая пересекается с другим лежащим в другой плоскости прямым.

14. Есть три плоскости F, L, O. Плоскость F является параллельной плоскости O, плоскость L – параллельной плоскости O. Исходя из этого выберите правильное утверждение:

— Плоскость F и плоскость L перпендикулярны.

— Плоскость F и плоскость L являются скрещивающимися.

+ Плоскость F и плоскость L параллельны.

— У плоскости F и плоскости L есть одна точка пересечения.

15. При условии, что прямые P и R параллельны третьей прямой Q,:

— прямая P будет перпендикулярна прямой R.

— прямая P и прямая R будут иметь одну точку пересечения.

— прямые P и R будут скрещивающимися.

+ прямые P и R будут параллельны между собой.

16. Есть две параллельные прямые и две параллельные плоскости. Между двумя данными плоскостями находятся отрезок XX1 и отрезок ZZ1 параллельных прямых. Выберите правильное утверждение:

— XX1 и ZZ1 имеют точку пересечения

17. Сколько параллельных прямых можно провести через точку, находящуюся вне данной прямой?

18. В каком варианте представлен ответ с ошибочным суждением?

— Две плоскости считаются параллельными, если каждая из них параллельна третьей плоскости.

— Две параллельные линии могут образоваться в результате пересечения двух параллельных плоскостей третьей плоскостью.

+ Две пересекающиеся прямые, находящиеся в одной плоскости, называются параллельными.

— Отрезки двух параллельных прямых, заключенные между двумя параллельными плоскостями, всегда равны друг другу.

19. Дана трапеция ABCD, основа CD которой лежит в плоскости α. KN – средняя линия трапеции. Выберите вариант ответа, в котором указано правильное суждение:

— KN находится в плоскости α.

+ KN параллельна плоскости α.

— KN перпендикулярна плоскости α.

-KN параллельна AD.

тест-20. Точка N находится вне данной плоскости. Можно ли через нее провести плоскость, параллельную данной? Если да, то сколько?

21. Выберите вариант ответа, в котором представлено правильное продолжение следующего утверждения: «Если S – это середина стороны AB треугольника ABC, сторона AC которого находится в плоскости α, то . »:

— через точку S можно провести две прямые, которые будут параллельны плоскости α.

— прямая SC и плоскость α перпендикулярны.

+ через точку S можно провести лишь одну параллельную плоскости α плоскость.

— через точку S нельзя провести прямую, которая будет перпендикулярна плоскости α.

22. Прямая H лежит вне плоскости a и является параллельной с прямой J, которая находится в данной плоскости. Выберите ошибочное суждение:

— Прямая H и прямая J не пересекаются.

+ Прямая H и прямая J перпендикулярны.

— Прямая J и плоскость a параллельны.

— Прямая H параллельна плоскости a.

23. Выберите ошибочное утверждение:

+ У прямой и плоскости может быть лишь одна общая точка.

— Две параллельные плоскости никогда не будут пересекаться.

— В одной плоскости могут лежать любые пять точек.

— В одной плоскости могут находиться две параллельные прямые.

24. Прямая M и плоскость α не имеют ни одну общую точку. Это значит, что:

— прямая M пересекается с другой прямой, лежащей в плоскости α.

— прямая M и плоскость α пересекаются.

— в плоскости α лежит прямая M.

+ плоскость α и прямая M параллельны.

25. Что является пересечением двух плоскостей в пространстве?

26. Выберите вариант ответа, в котором неправильно указано продолжение следующей фразы: «Плоскость α и β являются параллельными между собой. Прямая K не лежит в плоскости α»:

+ Прямая K и плоскость β имеют одну общую точку пересечения.

— Прямая K лежит в плоскости β.

— Прямая K и плоскость β являются параллельными.

— Прямая K и плоскость α являются параллельными.

27. Какими могут быть две плоскости в пространстве?

— пересекающимися или скрещивающимися

+ параллельными или пересекающимися

28. Плоскость β пересекается с плоскостью α. Выберите правильное утверждение:

— Плоскость β перпендикулярна линии пересечения плоскостей α и β.

— Плоскость α является перпендикулярной линии пересечения плоскостей α и β.

— Плоскость β и плоскость α являются параллельными.

+ Одна из этих плоскостей параллельна линию пересечения плоскостей α и β.

29. Выберите вариант ответа, в котором указано неправильное продолжение следующей фразы: «Боковые стороны треугольника ABC параллельны плоскости β. Значит, . »:

+ основание треугольника и плоскость β пересекаются.

— плоскость треугольника и плоскость β параллельны.

— основание треугольника и плоскость β являются параллельными.

— основание треугольника и плоскость β не пересекаются.

тест_30. Посмотрите на рисунок и скажите, сколько параллельных плоскостей можно провести через две прямые?

Видео:10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Выберете верное утверждение : а)если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая лежит в данной плоскости ; б)если плоскость альфа проходит через прямую, параллельн?

Геометрия | 10 — 11 классы

Выберете верное утверждение : а)если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая лежит в данной плоскости ; б)если плоскость альфа проходит через прямую, параллельную плоскости бета, то и плоскость альфа параллельна плоскости бета ; в)если две прямые пересекают плоскость, то они параллельны ; г)прямая и плоскость называется параллельными, если они не имеют общих точек.

Г)прямая и плоскость называется параллельными, если они не имеют общих точек.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Прямая а лежит в плоскости альфа и параллельна плоскости бета?

Прямая а лежит в плоскости альфа и параллельна плоскости бета.

Прямая б параллельна плоскостям альфа и бета.

При каком взаимном расположении данных прямых можно утверждать, что альфа параллельна бета?

Видео:10 класс, 2 урок, Аксиомы стереометрииСкачать

Плоскости альфа и бета параллельны?

Плоскости альфа и бета параллельны.

А — точка плоскости альфа.

Докажите, что любая прямая, проходящая через точку А и параллельная плоскости бета, лежит в плоскости альфа.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Плоскости Альфа и Бета пересекаются по прямой С?

Плоскости Альфа и Бета пересекаются по прямой С.

Плоскость Омега, параллельная прямой С, пересекает плоскости Альфа и Бета по прямым а и b соответственно.

Докажите, что a параллельна Бета и b параллельна Альфа.

Видео:10 класс, 10 урок, Параллельные плоскостиСкачать

Прямая а параллельна плоскости альфа?

Прямая а параллельна плоскости альфа.

Через прямую а проведена плоскость бэта, пересекающая плоскость альфа по прямой b.

В плоскости альфа существует прямая с , которая параллельна а.

Докажите, что b параллельна c.

Видео:Параллельность прямых. 10 класс.Скачать

Прямые a и b параллельны?

Прямые a и b параллельны.

Прямая a параллельна плоскости альфа, прямая b параллельна плоскости бета.

Как могут расположены плоскости?

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Выберите верные утверждения?

Выберите верные утверждения.

А) Прямая, не лежащая в данной плоскости и параллельная какой либо прямой на плоскости, параллельна самой плоскости.

Б) Плоскость, проходящая через одну из двух параллельных прямых, параллельна другой прямой.

В) Через точку, не принадлежащую плоскости, можно провести бесконечное число прямых, параллельных данной плоскости.

Г) Через одну из двух параллельных прямых можно провести плоскость, параллельную другой прямой, и только одну.

Д) Если две прямые параллельны одной плоскости, то они параллельны друг другу.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Плоскости альфа и бета параллельны?

Плоскости альфа и бета параллельны.

В плоскости альфа проведена прямая А, в плоскости бета — прямая В.

Верно ли что эти прямые не имеют общих точек?

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Плоскости альфа и бета параллельны, причем альфа пересекает некоторую прямую а?

Плоскости альфа и бета параллельны, причем альфа пересекает некоторую прямую а.

Докажите, что и плоскость бета пересекает прямую а.

Видео:10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Плоскость бета пересекает прямую а , параллельную плоскости альфа?

Плоскость бета пересекает прямую а , параллельную плоскости альфа.

Докажите, что плоскости бета и альфа пересекаются.

Видео:10 класс, 17 урок, Признак перпендикулярности прямой и плоскостиСкачать

(Помогите) Плоскости альфа и бета параллельны, причем плоскость альфа пересекает некоторую прямую а?

(Помогите) Плоскости альфа и бета параллельны, причем плоскость альфа пересекает некоторую прямую а.

Докажите, что и плоскость бета пересекает прямую а.

На этой странице сайта вы найдете ответы на вопрос Выберете верное утверждение : а)если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая лежит в данной плоскости ; б)если плоскость альфа проходит через прямую, параллельн?, относящийся к категории Геометрия. Сложность вопроса соответствует базовым знаниям учеников 10 — 11 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

Противоположные стороны параллелограмма равны. Периметр — сумма четырех сторон, значит сумма двух разных сторон равна 32 : 2 = 16см. Из соотношения можно написать, что одна сторона равна Х, а вторая 3Х. Тогда 4Х = 16см, Х = 4см, а большая сторона ..

1. Нулевой вектор коллинеарен любому вектору : Если = (или = ), то||(или||). 2. Нулевой вектор одинаково направлен с любым вектором, . 3. Любые два коллинеарных вектора можно отложить на одной прямой. Достаточно отложить векторы от одной точки. 4..

Угол N = M = 35 Угол О = 180 — (35 + 35) = 110.

15″ = 10″ + х» х» = 15″ — 10″ х = 5 S = 1 / 2 высоты * на сторону, к которой она проведена S = 1 / 2 * 5 * 10 S = 25 см2 » — квадрат ( 15″ — 15 в квадрате).

Дано : АВС , АВ = ВС = 15 см АС = 10Найти : S — ? Решение : Высота, опущенная из вершины равнобедренного треугольника на его основание является одновременно и высотой, и медианой. ВН — высотаАН = НС = 5 смТреугольник АВН — прямоугольный, катет АН =..

Только если в общем виде , если будет. Дан угол прорстро получать и посчитай.

Ииосноваа Х сотая ле врмпо флтсяаходции аходции адь трапплощадей.

DOA по двум углам (накрест лежащим) , BO : OD = OC : AO = BC : AD = 2 : 3 2AO = 3OC AO + OC = 20 2AO + 2OC = 40 5OC = 40 OC = 8 AO = 12.

OB = OA, OC = CO(общая сторона), AC = BC.

1)тр. АОС = тр. ОСВ (по двум катетам) = > АС = ВС(соотв. Элементы).

📸 Видео

6. Параллельность прямой и плоскостиСкачать

10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать

19 задание огэ математика 2023 ВСЕ ТИПЫ геометрияСкачать

Параллельность прямых, плоскостей, прямой и плоскости | Математика ЕГЭ для 10 класса | УмскулСкачать

№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

Параллельность прямой к плоскостиСкачать

ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ 10 класс стереометрияСкачать

Аксиомы стереометрии и их следствия. 10 класс.Скачать