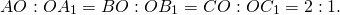Как построить циркулем медиану треугольника (6 видео)

Медиана треугольника

Что называется медианой треугольника?

Определение.

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Как построить медиану треугольника?

Чтобы построить медиану треугольника , надо:

1) С помощью линейки найти и отметить середину стороны треугольника.

2) Соединить полученную точку с вершиной, лежащей напротив этой стороны.

Рисунок медианы треугольника:

Как построить медиану треугольника с помощью циркуля и линейки без шкалы, мы рассмотрим позже, в теме «Построить треугольник».

Сколько медиан имеет треугольник?

Так как у треугольника три вершины и три стороны, то и отрезков, соединяющих вершину и середину противолежащей стороны, тоже три. Значит, треугольник имеет три медианы.

Все три медианы треугольника пересекаются в одной точке:

Точка пересечения медиан называется центром тяжести треугольника.

В точке пересечения медианы треугольника делятся в отношении два к одному, считая от вершины:

Об этом свойстве медиан треугольника, а также о том, как найти длину медианы через длины сторон треугольника, более подробно мы поговорим позже и рассмотрим, как свойства медианы использовать при решении задач.

Кроме того, отдельно будут рассмотрены медиана прямоугольного треугольника, проведенная к гипотенузе и медиана равнобедренного треугольника, проведенная к его основанию, поскольку каждая из них обладает своими свойствами, которые надо знать и уметь применять.

Видео:№154. Дан треугольник ABC. Постройте: а) биссектрису АК; б) медиану ВМ; в) высоту СН треугольника.Скачать

Построения циркулем и линейкой

С помощью линейки можно провести произвольную прямую, а также построить прямую, проходящую через две данные точки (в данном случае мы говорим о линейке без масштабных делений). С помощью циркуля можно провести окружность произвольного радиуса, а также окружность с центром в данной точке и радиусом, равному данному отрезку. Эти операции помогают решать задачи на построение:

построить отрезок, равный данному;
построить угол, равный данному;
построить биссектрису угла,
через данную точку провести прямую, перпендикулярную к данной прямой;
разделить данный отрезок пополам, т.е. найти середину данного отрезка и т.д.

Пример:

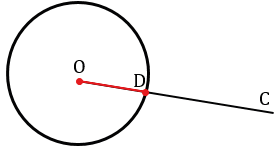
На данном луче от его начала отложить отрезок, равный данному.

Дано: луч ОС, отрезок АВ.

Построить: отрезок ОD = ОА.

Решение:

Строим с помощью линейки произвольные отрезок АВ и луч ОС.

Далее прикладываем циркуль к отрезку АВ так, чтобы его игла стояла на одном конце отрезка, а грифель карандаша на другом, тем самым получаем раствор циркуля, равный отрезку АВ. Затем, не меняя раствор циркуля, прикладываем его иглой к точке О луча ОС и строим окружность (всю окружность строить необязательно, достаточно той ее части, которая пересекает луч АС), получаем окружность радиуса АВ с центром в точке О.

Точу пересечения данной окружности с лучом ОС обозначим D. Получаем отрезок ОD — искомый отрезок, т.е. ОD = ОА.

Поделись с друзьями в социальных сетях:

Видео:Построение медианы в треугольникеСкачать

Пошаговое построение медианы, биссектрисы медианы в треугольнике с помощью циркуля

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Поэтому, для построения медианы необходимо выполнить следующие действия:

1) найти середину стороны;

2) соединить точку, являющуюся серединой стороны треугольника, с противолежащей вершиной отрезком — это и будет медиана.

Биссектриса треугольника — это отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне. Поэтому, для построения биссектрисы необходимо выполнить следующие действия:

1) построить биссектрису какого-либо угла треугольника (а биссектриса угла — это луч, выходящий из вершины угла и делящий его на две равные части);

2) найти точку пересечения биссектрисы угла треугольника с противоположной стороной;

3) соединить вершину треугольника с точкой пересечения на противоположной стороне отрезком — это и будет биссектриса.

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противоположную сторону. Поэтому, для построения высоты необходимо выполнить следующие действия:

1) провести прямую, содержащую одну из сторон треугольника (в случае, если проводится высота из вершины острого угла в тупоугольном треугольнике);

2) из вершины, лежащей напротив проведенной прямой, опустить перпендикуляр к ней ( а перпендикуляр — это отрезок, проведенный из точки к прямой, составляющей с ней угол 90 градусов) — это и будет высота.

Задание для самостоятельной проверки.

1 вариант: Построить медиану остроугольного треугольника.

2 вариант: Построить медиану тупоугольного треугольника.

3 вариант: Построить медиану прямоугольного треугольника.

4 вариант: Построить биссектрису остроугольного треугольника.

5 вариант: Построить биссектрису тупоугольного треугольника.

6 вариант: Построить биссектрису прямоугольного треугольника.