Софизм — доказательство ложного утверждения, причем ошибка в доказательстве искусно замаскирована. Софистами называли группу древнегреческих философов IV-V вв. до н.э., достигших большого искусства в логике. Приведем пример софизма. Если равны половины, то равны и целые. Полуполное есть то же, что и полупустое, значит, полное-то же самое, что пустое. К софизмам можно отнести доказательство того, что Ахиллес, бегущий в 10 раз быстрее черепахи, не сможет ее догнать.
Пусть черепаха на 100 м впереди Ахиллеса. Когда Ахиллес пробежит эти 100 м, черепаха будет впереди него на 10 м. Пробежит Ахиллес эти 10 м, а черепаха окажется впереди на 1 м и т.д. Расстояние между ними все время сокращается, но никогда не обращается в нуль. Значит, Ахиллес никогда не догонит черепаху. А вот два математических софизма.
«Доказательство», что все числа равны между собой.
Пусть а и b — произвольные числа и пусть а > b, тогда существует такое положительное число с, что а = b + с. Умножим это равенство на а — b и преобразуем полученное равенство:
а 2 — аb = аb + ас — b 2 — bс,
а 2 — аb — ас = аb — b 2 — bс,
а(а — b — с) = b(а — b — с).
Разделив обе части полученного равенства на (а — b — с), получим, что а = b. Ошибка здесь находится в самом конце, когда мы делили на число (а — b — с), которое равно нулю.
«Доказательство», что все треугольники — равнобедренные.
Рассмотрим произвольный треугольник АВС (рис. 1). Проведем в нем биссектрису угла В и серединный перпендикуляр к стороне АС. Точку их пересечения обозначим через O. Из точки О опустим перпендикуляр ОD на сторону АВ и перпендикуляр ОЕ на сторону ВС. Очевидно, что ОА = ОС и OD = ОЕ. Но тогда прямоугольные треугольники АОD и СОЕ равны по катету и гипотенузе. Поэтому ∠DАО = ∠ЕСО. В то же время ∠ОАС = ∠ОСА, так как треугольник АОС — равнобедренный. Получаем: ∠ВАС = ∠ОАО + ∠ОАС = ∠ЕСО + ∠ОСА = ∠ВСА.
Итак, угол ВАС равен углу ВС А, поэтому треугольник AВС-равнобедренный: АВ = ВС.
Здесь ошибка в чертеже. Серединный перпендикуляр к стороне и биссектриса противоположного ей угла для неравнобедренного пересекаются вне этого треугольника.
И еще один пример софизма.
Посмотрите на рис.2. Прямоугольники явно равносоставлены, но площадь одного равна 64 клеткам, а площадь другого – 65. И здесь ошибка в чертеже! Точки В, Е, F, D не лежат на одной прямой, а являются вершинами очень узкого параллелограмма, площадь которого равна площади одной клетки – той самой лишней клетки.
Видео:Все треугольники – равнобедренные (софизм)Скачать
Все треугольники равнобедренные софизм
Пусть ABC — произвольный треугольник (рис.1 или 2 или 3); проведем биссектрису угла C, затем ось симметрии стороны AB (т.е. прямую, перпендикулярную к AB в середине M отрезка AB) и рассмотрим различные случаи взаимного расположения этих прямых; так как в рассуждениях участвуют только одна биссектриса и одна ось симметрии, то разрешим себе их называть просто «биссектриса» и «ось».
Случай 1: биссектриса и ось не пересекаются ,
т.е. либо параллельны, либо сливаются. Так как ось перпендикулярна к AB, т.е. совпадает с высотой, а в таком случае треугольник ABC — равнобедренный (CA=CB).
Случай 2: биссектриса и ось не пересекаются внутри
треугольника ABC
(рис.1), пусть в точке N. Так как эта точка равноудалена от сторон угла ACB, то, опустив из нее перпендикуляры NP и NQ соответственно на CB и CA, имеем NP=NQ.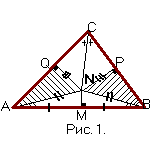 
Но точка N в тоже время равноудалена от концов отрезка AB, т.е. NB=NA. Прямоугольные треугольники NPB и NQA равны по катету и гипотенузе, следовательно, угол NAQ равен углу NBP. Прибавляя к этим равным углам равные между собой (как углы при основании равнобедренного треугольника ANB) углы NAB и NBA, получим угол CAB, равный углу CBA, значит, треугольник ABC — равнобедренный (именно CA=CB).
Случай 3: биссектриса и ось пересекаются на стороне AB ,
т.е. в середине M этой стороны. Это означает, что в треугольнике ABC медиана и биссектриса, проведенные из вершины C, совпадают, а отсюда следует, что этот треугольник- равнобедренный.
Замечание.
Предостерегаем читателя от возможной ошибки. Хорошо известно, что в равнобедренном треугольнике медиана и биссектриса совпадают. Но мы ссылаемся здесь не не это, а на обратное утверждение: «если в треугольнике медиана и биссектриса , проведенные из одной вершины, совпадают, то треугольник — равнобедренный». В такой формулировке обратная теорема также верна, но доказательство ее может затруднить читателя, поэтому приводим одно из возможных. Пусть в треугольнике ABC отрезок CM — одновременно медиана и биссектриса. Опустив из точки M перпендикуляры MP и MQ на стороны CB и CA (можно воспользоваться рис. 1, считая там точки M и N совпадающими; при этом прямая MN становится лишней), получаем равные прямоугольные треугольники MPB и MQA, а затем из равенства углов MBP и MAQ заключаем, что треугольник ABC — равнобедренный. Это рассуждение будет неполным, если не показать, что точки P и Q попадут именно на стороны CB и CA, а не на их продолжения. Одна из точек могла бы попасть на продолжение соответсвующей стороны, если бы один из углов A и B был тупым. Пусть, например, угол B — тупой, так что точка P лежит на продолжении стороны CB; по-прежнему получается угол MAQ равен углу MBP, но теперь это приводит к противоречию, так как первый из этих углов — внутренний для треугольника ABC, а второй — внешний, с первым не смежный.
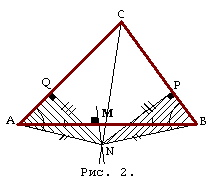
Случай 4а: биссектриса и ось пересекаются вне треугольника ABC; перпендикуляры, опущенные из точки N пересечения на стороны CB и CA, падают на эти стороны (рис. 2), а не на их продолжения.
Как и раньше, получаем равные треугольники NPB и NQA, равнобедренный треугольникANB. Углы при основании AB треугольника ABC равны теперь как разности (а не как суммы в случае 2) соответственно равных углов.
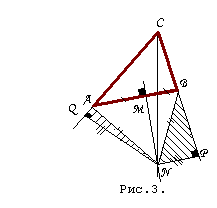
Случай 4б: биссектриса и ось пересекаются вне треугольника ABC; перпендикуляры, опущенные из точки N переечения на стороны CB и CA , падают на продолжение этих сторон (рис. 3).
Те же построения и рассуждения приводят к выводу о равенстве внешних углов при вершинах A и B треугольника ABC. Отсюда сейчас же вытекает равенство внутренних углов A и B, следовательно, CA=CB.
Анализ примера.
Рассмотрены не все возможные случаи (Здесь и дальше, говоря о возможных допущениях или о возможных случаях, мы вовсе не утверждаем, что все они действительно возможны в условиях данного примера. Наоборот, не раз случается, что допущенный нами сначала в качестве возможного случай потом окажется фиктивным, т.е. противоречащим условию или тому, что считается установленным, как это часто бывает в доказательствах «от противного». Таким образом, речь идет всегда о так называемых «априорных возможностях » (от a priori- заранее), т.е. о возможностях, которые представляются заранее, до учета остальных условий вопроса. ), именно не учтена возможность того, что из двух перпендикуляров NP и NQ один упадет на сторону треугольника ABC, а другой — на продолжение стороны (рис. 4, где пока не надо принимать во внимание окружность). Если это произойдет, то один из углов при основании AB треугольника ABC окажется разностью двух углов, а другой будет смежным для суммы тех же углов — отсюда, разумеется, никаких выводов, относящихся к углам при основании, а значит, и к равенству боковых сторон, сделать нельзя. Достаточно установить этот пробел в доказательстве, для того чтобы оно было опорочено. Более того, если данный треугольник — неравнобедренный, то можно утверждать (рассуждая от противного), что все рассмотренные случаи (рис. 1, 2 и 3) невозможны, а единственно возможный случай (рис. 4) упущен.
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать
Все треугольники — равнобедренные ! | Логические задачи
И вот доказательство:
В произвольном треугольники проведём серпер (серединный перпендикуляр — примечание) к стороне AC и биссектрису угла В. Точку их пересечения обозначим О
Далее соединим точку О с точками А и В, а так же проведём из неё перпендикуляры на стороны треугольника.
Прямоугольные треугольники АОН и СОН равны по двум катетам. Из их равенства следует, что ОА=ОС
Прямоугольные треугольники ВОN и ВОМ равны по гипотенузе и острому углу. Из их равенства следует, что ON=OM и BN=BM
Прямоугольные треугольники АОN и COM равны по катету и гипотенузе (OA=OC и ON=OM). Из их равенства следует, что АN=CM
Т.к. AN=CM и BN=BM, то AN+NB=BM+MC или AB=BC. Итак, любой треугольник — равнобедренный!
Но вы спросите меня, а что если биссектриса и серпер пересекутся за пределами треугольника? Вот ответ:
Ну так вот. Проводим все те же построения, что и в предыдущем случае. Только теперь перпендикуляры упадут на продолжения сторон.
Прямоугольные треугольники ВОN и BOM равны по гипотенузе и острому углу => BN=BM и ON=OM
Прямоугольные треугольники AОH и COH равны по двум катетам => OА=OС
Прямоугольные треугольники АОN и COM равны по катету и гипотенузе (OA=OC и ON=OM). Из их равенства следует, что АN=CM
Т.к. AN=CM и BN=BM, то NB-АN=BM-CM или AB=BC. Итак, любой треугольник — равнобедренный!
И снова находчивый читатель недоволен. А что если серпер и биссектриса пересекаются за пределом треугольника, но перпендикуляры падают на стороны треугольника, а не их продолжения? Вот что:
Опять построения те же.
Прямоугольные треугольники ВОN и BOM равны по гипотенузе и острому углу => BN=BM и ON=OM
Прямоугольные треугольники AОH и COH равны по двум катетам => OА=OС
Прямоугольные треугольники АОN и COM равны по катету и гипотенузе (OA=OC и ON=OM). Из их равенства следует, что АN=CM
Т.к. AN=CM и BN=BM, то BN+NA=BM+MC или AB=BC. Итак, любой треугольник — равнобедренный!
на сей раз окончательно и безповоротно 🙂
Видео:Все треугольники равнобедренные. Вообще все.Скачать
Все треугольники — равнобедренные ! | Логические задачи: 5 комментариев
Мой самый люимый софизм 🙂
Собственно первый софизм, с которым я столкнулся
📺 Видео
Софизмы в геометрииСкачать
Виды треугольниковСкачать
7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать
✓ Свойства и признаки равнобедренного треугольника | Ботай со мной #008 | Борис ТрушинСкачать
Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать
Свойства равнобедренного треугольника. 7 класс.Скачать
На ЕГЭ 2021 по математике все ТРЕУГОЛЬНИКИ будут РАВНОБЕДРЕННЫЕСкачать
Равнобедренный треугольник. 7 класс.Скачать
Все треугольники равнобедренные. ДоказательствоСкачать
СОФИЗМЫ / Пустое и полное / Ахиллес и черепаха / Все числа равныСкачать
Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать
ГЕОМЕТРИЧЕСКИЙ СОФИЗМСкачать
Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать
Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать
Признаки равенства треугольников. 7 класс.Скачать
Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать
7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать
