Расстояние от центра вписанной в равнобедренную трапецию окружности

Геометрия | 5 — 9 классы

Расстояние от центра вписанной в равнобедренную трапецию окружности до концов боковой стороны равны 9 и 12см.

Найдите площадь трапеции.

АД и ВС — основания

О центр вписанной окр.

Треугольник СОД прямоугольный ОС = 9, ОД = 12, СД = 15(т.

r = ОР — высота на СД

r = ОР = ОС * ОД / СД = 9 * 12 / 15 = 7, 2

4 — высота пирамиды

S = (ВС + АД) * h / 2 = (АВ + СД) * h / 2 = (15 + 15) * 14, 4 / 2 = 216.

Видео:Задача про трапецию, описанную около окружностиСкачать

В равнобедренную трапецию площадью 28 вписана окружность радиуса 2?

В равнобедренную трапецию площадью 28 вписана окружность радиуса 2.

Найдите боковую сторону трапеции.

Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

Дана равнобедренная трапеция, её площадь равна 125?

Дана равнобедренная трапеция, её площадь равна 125.

В трапецию вписана окружность так, что расстояние между точками касания её боковых сторон равно 8.

Найдите радиус окружности, вписанной в трапецию.

Видео:Задание 26 Равнобедренная трапеция Окружность, вписанная в треугольникСкачать

Центр окружности, вписанной в прямоугольную трапецию, удалён от концов её боковой стороны на расстояния 15 и 20?

Центр окружности, вписанной в прямоугольную трапецию, удалён от концов её боковой стороны на расстояния 15 и 20.

Найдите стороны трапеции.

Видео:Трапеция и вписанная окружностьСкачать

Радиус окружности, вписанной в равнобочную трапецию, равен 3, а площадь трапеции равна 108?

Радиус окружности, вписанной в равнобочную трапецию, равен 3, а площадь трапеции равна 108.

Найдите расстояние между точками касания окружности боковых сторон трапеции.

Видео:Планиметрия 19 | mathus.ru| расстояние от центра окружности до точки пересечения диагоналей трапецииСкачать

Окружность вписана в равнобедренную трапецию, площадь которой равна 64 см2?

Окружность вписана в равнобедренную трапецию, площадь которой равна 64 см2.

Найдите боковую сторону трапеции (а), если острый угол при основании трапеции равен 30 градусов.

Видео:Окружность, вписанная в трапециюСкачать

В трапеции расстояние от центра вписанной в нее окружности до концов боковой стороны равны 75 и 100 см а до концов меньшего основания 65 и 75 см ?

В трапеции расстояние от центра вписанной в нее окружности до концов боковой стороны равны 75 и 100 см а до концов меньшего основания 65 и 75 см .

Найдите площадь трапеции.

Видео:Задание 26 Равнобедренная трапеция Окружности, вписанные в треугольникиСкачать

ЗАДАЧА №1?

В равнобедренную трапецию вписана окружность.

Найдите периметр трапеции, если одна из её боковых сторон равна 14.

Видео:Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать

В равнобедренную трапецию вписана окружность радиуса 2?

В равнобедренную трапецию вписана окружность радиуса 2.

Найдите площадь трапеции если длинна боковой стороны равна 10.

Видео:Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать

В равнобедренную трапецию с боковой стороной, равной 10 м, вписана окружность радиуса 3 м?

В равнобедренную трапецию с боковой стороной, равной 10 м, вписана окружность радиуса 3 м.

Найдите площадь трапеции.

Видео:Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

Решите задачу : В равеобедренную трапецию вписана окружность Площадь трапеции 125 Хорда, проходящая над центром, и соединяющая боковые стороны трапеции равна 8 Найдите площадь круга?

Решите задачу : В равеобедренную трапецию вписана окружность Площадь трапеции 125 Хорда, проходящая над центром, и соединяющая боковые стороны трапеции равна 8 Найдите площадь круга.

На этой странице находится вопрос Расстояние от центра вписанной в равнобедренную трапецию окружности до концов боковой стороны равны 9 и 12см?. Здесь же – ответы на него, и похожие вопросы в категории Геометрия, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 5 — 9 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.

10 задание : Угол САО = 40градусов Угол АСО = 40градусов В треугольнике 180 градусов УГЛЫ САО + АСО = 80 градусов 40 + 40 = 80 градусов Решение : 180 — 80 = 100 градусов УГОЛ СОА = 100 градусов Ответ : 100 градусов.

Точка пересечения диагоналей прямоугольника является центром описанной вокруг него окружности. Диагональ (d) в данном случае складывается из двух радиусов описанной окружности. D = 2R = 50 Сумма квадратов диагоналей прямоугольника равна сумме квадр..

Видео:Задание 16 ОГЭ по математике. Окружность вписана в трапецию.Скачать

Расстояние от центра вписанной в равнобедренную трапецию окружности

Ответ оставил Гость

Вся «хитрость» в том, что эти отрезки 9 и 12 — перпендикулярны, как биссектрисы внутренних односторонних углов. Сумма внутренних односторонних углов 180 градусов, значит сумма половин — 90, поэтому треугольник, образованный боковой стороной и этими отрезками — прямоугольный.

Ясно, что это «египетский» треугольник со сторонами 9,12,15, и высота его равна 9*12/15 = 36/5; (это — радиус окружности, вписанной в трапецию).

Трапеция равнобедренная и в неё вписана окружность, следовательно, ПОЛУпериметр равен р = 15*2 = 30; радиус окружности равен вычисленной высоте треугольника r = 36/5, и площадь S = p*r = 30*36/5 = 36*6 = 216;

Видео:Математика ОГЭ. Задание №25. Окружность, вписанная в равнобедренную трапецию.Скачать

В равнобедренную трапецию вписана окружность. Расстояние от центра окружности до точки пересечения диагоналей трапеции относится к радиусу, как 3 : 5. Найдите отношение периметра трапеции к длине вписанной окружности.

Пусть O — центр окружности, P — точка касания с боковой стороной AB, F и T — точки касания окружности с основаниями AD и BC, M — середина AB, K — точка пересечения диагоналей AC и BD трапеции. Обозначим OK = 3x, OP = 5x.

Поскольку AP : PB = AF : BT = AK : KC, то KP || BC || OM. Из прямоугольного треугольника OKP находим, что KP = 4x. Из подобия треугольников OKP и MPO находим, что

OM = = .

Тогда периметр трапеции равен 8OM = 50x. Следовательно, искомое отношение равно

= .

Ответ

.

🎬 Видео

Геометрия Под каким углом видна боковая сторона трапеции из центра вписанной окружностиСкачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Планиметрия 27 | mathus.ru | окружность, касающаяся основания трапеции и вписанной в нее окружностиСкачать

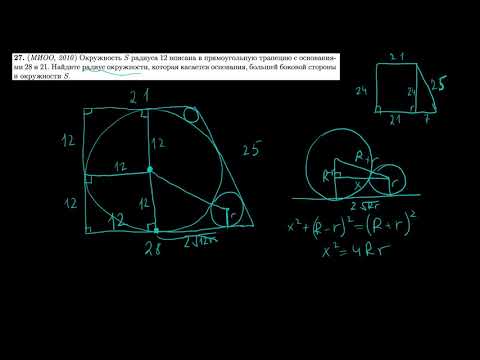
Окружность и трапеция | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис Трушин +Скачать

Радиус описанной окружности трапецииСкачать

Центр вписанной окружности равнобедренного ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Всегда ли трапеция вписанная в окружность РАВНОБЕДРЕННАЯ? Задача. ЕГЭ, ОГЭ.Скачать

ТЕСТ НА ЭРУДИЦИЮ и кругозор: МНОГО УМНЫХ ВОПРОСОВ, ответы знает не каждый. #насколькотыумный #тестСкачать