Два острых угла прямоугольного треугольника относятся как 4:5. Найдите больший острый угол. Ответ дайте в градусах.
Сумма острых углов прямоугольного треугольника равна 90°. Острые углы прямоугольного треугольника относятся как 4 части к 5 частям, сумма этих углов 4 + 5 = 9 частей. Поэтому одна часть равна 10°. Так как больший угол содержит в себе 5 частей, он равен 5·10° = 50°.
В треугольнике ABC угол C равен 90°, Найдите AB.
Так как треугольник ABC — прямоугольный, то . Имеем:
В треугольнике ABC угол C равен 90°, . Найдите AB.
Так как треугольник ABC — прямоугольный, то . Имеем:
Аналоги к заданию № 311387: 311399 311498 311500 Все
Катеты прямоугольного треугольника равны 35 и 120. Найдите высоту, проведенную к гипотенузе.
Пусть катеты имеют длины a и b, а гипотенуза — длину Пусть длина высоты, проведённой к гипотенузе равна
Найдём длину гипотенузы по теореме Пифагора:
Площадь прямоугольного треугольника может быть найдена как половина произведения катетов или как половина произведения высоты, проведённой к гипотенузе на гипотенузу:
- Необходимый теоретический материал для успешной сдачи ОГЭ-9 по математике для учеников разной подготовленности
- 1. Углы
- 2. Медиана, биссектриса, высота
- 3. Треугольник
- 3. Четырехугольники
- 4. Окружность
- Прямоугольные треугольники
- Некоторые свойства прямоугольного треугольника:
- Соотношение между сторонами и углами в прямоугольном треугольнике:
- Значения тригонометрических функций некоторых углов:
- 🔥 Видео
Видео:Все типы 15 задания ОГЭ 2022 математика | Геометрия на ОГЭСкачать

Необходимый теоретический материал для успешной сдачи ОГЭ-9 по математике для учеников разной подготовленности
Класс: 9
Ключевые слова: математика , ОГЭ
1. Углы
Вертикальные углы равны (на рис. 1 и 3; 6 и 8 и др.).
Внутренние накрест лежащие углы при параллельных прямых и секущей равны. (на рис. 4 и 6; 1 и 7).
Сумма внутренних односторонних углов при параллельных прямых и секущей равна 180˚ (на рис. 4 и 7; 1 и 6).
Соответственные углы при параллельных прямых и секущей равны. (на рис. 3 и 7; 1 и 5 и др.).
Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая перпендикулярна третьей прямой.
2. Медиана, биссектриса, высота
Биссектриса треугольника — отрезок, соединяющий вершину треугольника с точкой на противоположной стороне и делящий угол треугольника пополам.
Высота треугольника – перпендикуляр опущенный из вершины угла на противоположную сторону.
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
В любом треугольники все биссектрисы пересекаются в одной точке, все медианы пересекаются в одной точке, все медианы пересекаются в одной точке.
3. Треугольник
Сумма углов в любом треугольнике 180˚.
Средняя линия треугольника – прямая проходящая через середины двух сторон. Средняя линия параллельна одной из сторон и равна половине этой стороны.
Виды треугольников: тупоугольный (один угол тупой), прямоугольный (один угол прямой 90˚), остроугольный (все углы острые, меньше 90˚).
Равнобедренный треугольник — треугольник, у которого равны две стороны.
Свойства равнобедренного треугольника:
- в равнобедренном треугольнике углы при основании равны;
- в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;
Равносторонний треугольник — треугольник, у которого все стороны равны. (все углы по 60 градусов)
Всякий равносторонний треугольник является равнобедренным, но не всякий равнобедренный — равносторонним.
Три признака равенства треугольников
I признак по двум сторонам и углу между ними
II признак (по стороне и прилежащим углам)
III признак (по трем сторонам)
Признаки подобия треугольников
I признак по двум равным углам
II признак по двум пропорциональным сторонам и углу между ними
III признак по трем пропорциональным сторонам
Площади подобных фигур относятся как коэффициент подобия в квадрате.
Объемы подобных фигур относятся как коэффициент подобия в кубе.
Треугольник называется прямоугольным, если один из его углов прямой.
Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой. (самая большая сторона это гипотенуза, две др катеты).
Свойства прямоугольного треугольника
Сумма острых углов прямоугольного треугольника равна 90 градусов.
Катет, лежащий против угла в 30˚, равен половине гипотенузы.
Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.
Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности.
Теорема Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: a² + b² = c².
Пифагоровы тройки:
Признаки равенства прямоугольных треугольников
- По двум катетам.
- По гипотенузе и катету.
- По катету и прилежащему острому углу.
- По катету и противолежащему острому углу.
- По гипотенузе и острому углу.
Признаки подобия прямоугольных треугольников:
- По острому углу.
- По пропорциональности двух катетов.
- По пропорциональности катета и гипотенузы.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
Высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. Каждый из этих треугольников подобен исходному.
Высота прямоугольного треугольника: h=ab/c или h =
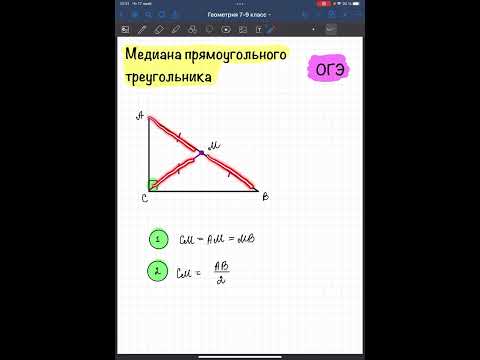
В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы: m=c/2 (R=с/2=mc).
3. Четырехугольники
Сумма углов в любом четырехугольнике 360˚.
Параллелограмм
Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны.
У параллелограмма противолежащие стороны равны и противолежащие углы равны.
Сумма любых двух соседних углов параллелограмма равна 180°.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Каждая диагональ делит параллелограмм на два равных треугольника.
Две диагонали параллелограмма делят его на четыре равновеликих треугольника.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Ромбом называется параллелограмм, у которого все стороны равны.
Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы прямые.
Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка.
Квадрат.
Квадрат – это прямоугольник, у которого все стороны равны.
Диагонали квадрата равны и перпендикулярны.
Сторона и диагональ квадрата связаны соотношениями: 
Трапеция
Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны.
Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
Средняя линия трапеции параллельна её основаниям и равна их полусумме.
Равнобокой называется трапеция, у которой боковые стороны равны.
У равнобокой трапеции: диагонали равны; углы при основании равны; сумма противолежащих углов равна 180.
Стороны и диагональ равнобокой трапеции связаны соотношением: d² = ab+c².
Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.
4. Окружность
Отрезок, соединяющий центр окружности с любой точкой окружности называется радиусом (r) окружности.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром окружности.
Прямая, имеющая с окружностью одну общую точку, называется касательной. Касательная и радиус проведенный в точку касания пересекаются под прямым углом.
Прямая, имеющая с окружностью две общие точки, называется секущей.
Центральный угол окружности – это угол, вершина которого лежит в центре окружности. Центральный угол равен дуге на которую он опирается.
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают ее. Вписанный угол равен половине дуги на которую опирается.
Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
Вписанный угол, опирающийся на диаметр равен 90˚.
Все вписанные углы, опирающиеся на одну и туже дугу равны.
Теорема косинусов:
Теорема синусов:
5. Формулы площадей
Видео:КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

Прямоугольные треугольники
Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | $/$ | $/$ | $/$ |
| $cosα$ | $/$ | $/$ | $/$ |
| $tgα$ | $/$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | $/$ |
Площадь прямоугольного треугольника равна половине произведения его катетов
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√$. Найдите косинус внешнего угла при вершине $В$.
Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то
Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:
Катет $ВС$ мы можем найти по теореме Пифагора:
Подставим найденное значение в формулу косинуса
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sinA=/, AC=9$. Найдите $АВ$.
Распишем синус угла $А$ по определению:
Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.
Применим теорему Пифагора, чтобы отыскать $«х»$
Так как длина $АВ$ составляет пять частей, то $3∙5=15$
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
🔥 Видео
Все о прямоугольных треугольниках | Математика ОГЭ – Дядя АртемСкачать

Всё про прямоугольный треугольник за 15 минут | Осторожно, спойлер! | Борис Трушин !Скачать

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК ОГЭ ЕГЭСкачать

Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

ОГЭ 2023 по математике. Все, что надо знать про прямоугольные треугольники. Решаем №15, 18, 23.Скачать

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Важное свойство прямоугольного треугольника #огэ #математика #огэматематика #данирСкачать

Медиана в прямоугольном треугольнике на ЕГЭ и ОГЭ по профильной математикеСкачать

Медиана прямоугольного треугольника— Геометрия ОГЭСкачать
ВЫСОТА ТРЕУГОЛЬНИКА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

ОГЭ как найти тангенс угла, если нет треугольника #математика #огэ #огэматематика #геометрияСкачать

Задание 15 #огэ #математика #shortsСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Что с углами. Прямоугольный треугольник #shortsСкачать

Свойство прямоугольного треугольника | Молодой репетиторСкачать

Свойства прямоугольного треугольника. 7 класс.Скачать







