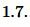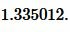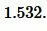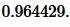С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
- 1. Радиус вписанной в треугольник окружности, если известна площадь и полупериметр треуольника
- 2. Радиус вписанной в треугольник окружности, если известны все три стороны треугольника
- 3. Радиус вписанной в треугольник окружности, если известны две стороны и угол между ними
- 4. Радиус вписанной в треугольник окружности, если известны сторона и прилежащие два угла
- Сторона равностороннего треугольника равна 10 3 найдите радиус окружности вписанной
- Как написать хороший ответ?
- Нахождение радиуса вписанной в треугольник окружности
- Формулы вычисления радиуса вписанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
- Примеры задач
- 🎥 Видео
Видео:Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

1. Радиус вписанной в треугольник окружности, если известна площадь и полупериметр треуольника
Пусть известна площадь S треугольника и полупериметр
| ( small p=frac ) | (1) |
где a, b, c стороны треугольника (Рис.1).
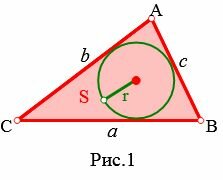 |
Найдем радиус вписанной в треугольник окружности r.
Из центра O вписанной в треугольник окружности проведем перпендикуляры к сторонам треугольника. Все эти перпендикуляры равны радиусу r вписанной в треугольник окружности (Рис.2).
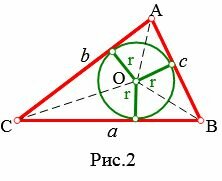 |
Прямыми OA, OB, OC разделим треугольник ABC на три треугольника: AOC, COB, AOB. Найдем площадь треугольников AOC, COB, AOB:
| ( small S_=frac cdot r cdot b ,) ( small S_=frac cdot r cdot c, ) ( small S_=frac cdot r cdot a ) | (2) |
| ( small S=S_+S_+S_)( small =frac cdot r cdot b ) ( small +frac cdot r cdot c ) ( small +frac cdot r cdot a ) ( small =frac cdot r cdot ( a+b+c) ) | (3) |
| ( small S=r cdot p. ) | (4) |
Найдем радиус r вписанной в треугольник окружности из равенства (4):
| ( small r=frac. ) | (5) |
Пример 1. Известны площадь ( small S=17 ) и полупериметр ( small p=10 ) треугольника. Найти радиус вписанной в треугольник окружности.
Решение. Для нахождения радиуса вписанной в треугольник окружности воспользуемся формулой (5).
Подставим значения ( small S=17 ) и ( small p=10 ) в (5):
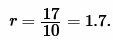 |
Ответ:
Видео:Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

2. Радиус вписанной в треугольник окружности, если известны все три стороны треугольника
Пусть известны три стороны треугольника: a, b, c. Найдем радиус вписанной в треугольник окружности (Рис.3).
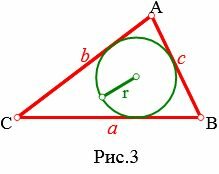 |
Площадь треугольника по трем сторонам вычисляется из формулы:
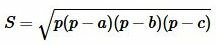 | (6) |
где полупериметр p вычисляется из формулы (1).
Подставляя (6) в (5), получим формулу радиуса вписанной в треугольник окружности:
| ( small r=sqrt<frac>, ) | (7) |
Пример 2. Известны стороны треугольника: ( small a=15 ,; b=7, ; c=9.) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник найдем сначала полупериметр треугольника из формулы (1):
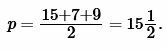 |
Подставим значения ( small a,; b, ; c, ; p ) в (7):
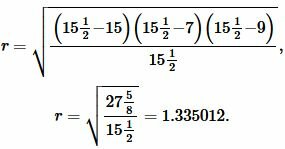 |
Ответ:
Видео:ОГЭ 2020 задание 17Скачать

3. Радиус вписанной в треугольник окружности, если известны две стороны и угол между ними
Пусть известны стороны b и c треугольника и угол A между ними (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.
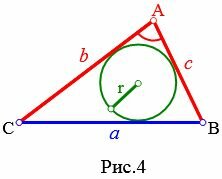 |
Из теоремы косинусов найдем сторону a треугольника:
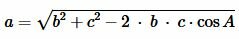 | (8) |
Далее, для вычисления радиуса вписанной в треугольник окружности, воспользуемся формулой (7), где полупериметр p вычисляется из (1).
Пример 3. Известны стороны треугольника: ( small b=9 ,; c=7, ; ) и угол меджу ними A=30°. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник найдем сначала сторону a треугольника из формулы (8):
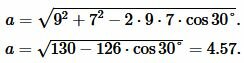 |
Далее найдем p из формулы (1):
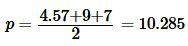 |
Подставим значения ( small a,; b, ; c, ; p ) в (7):
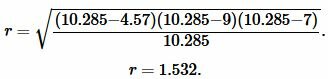 |
Ответ:
Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

4. Радиус вписанной в треугольник окружности, если известны сторона и прилежащие два угла
Пусть известны сторона a треугольника и прилежащие два угла B и C (Рис.5). Найдем радиус вписанной в треугольник окружности.
 |
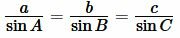 |
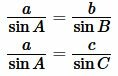 |
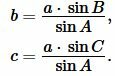 | (9) |
Поскольку сумма углов треугольника равна 180°, то имеем ( small angle A=180°-(angle B+angle C). ) Из формул приведения тригонометрических функций имеем: ( small sin A=sin (180°-( B+ C)) ) ( small =sin (B+C). ) Тогда формулы (9) можно переписать так:
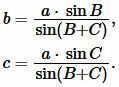 | (10) |
Получая значения сторон b, c из (10) и значение p из (1), можно найди радиус вписанной в треугольник окружности из формулы (7). Таким образом, для нахождения радиуса вписанной в треугольник окружности через сторону и прилежащим двум углам применяется формула
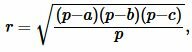 | (11) |
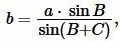 | (12) |
 , , | (13) |
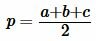 . . | (14) |
Пример 4. Сторона треугольника равена: ( small a=7 ,) а прилежащие два угла равны соответственно ( small angle B=25°, ) ( small angle C=40°, ) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11). Найдем, сначала, стороны b и c из формул (12),(13). Подставим значения ( small a=7 ,) ( small angle B=25°, ) ( small angle C=40°, ) в (12) и (13):
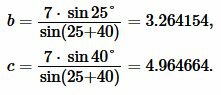 . . |
Далее найдем полупериметр p из формулы (14):
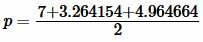 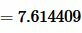 . . |
Подставляя значения a, b, c, p в (11), получим:
 |
Ответ:
Видео:Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту треугольникаСкачать
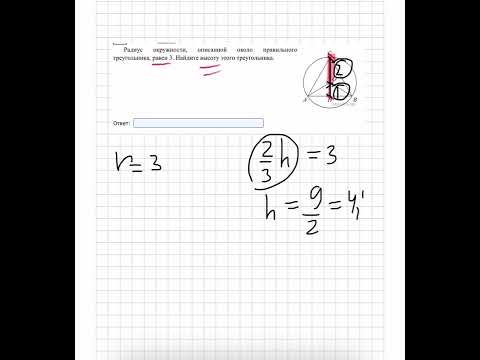
Сторона равностороннего треугольника равна 10 3 найдите радиус окружности вписанной
Вопрос по геометрии:
2. Около равностороннего треугольника описана окружность радиусом 10 корней из 3 см. Найдите радиус окружности, вписанной в этот треугольник
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Сторона равностороннего треугольника А3= R√3(через радиус описанной окружности). Значит, А3= 10√3*√3= 30.Сторона равностороннего треугольника А3 = 2r√3 (через радиус вписанной окружности).
Выражаем радиус вписанной окружности: r = А3 / 2√3r = 30 / 2√3 = 15/√3= 15√3/ 3 = 5√3
Ответ: радиус вписанной окружности равен 5√3.
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Видео:Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать

Нахождение радиуса вписанной в треугольник окружности
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в произвольный (любой), прямоугольный, равнобедренный или равносторонний треугольник. Также разберем примеры решения задач для закрепления представленного теоретического материала.
Видео:15 задание треугольники огэ по математике / маттаймСкачать

Формулы вычисления радиуса вписанной окружности
Произвольный треугольник
Радиус окружности, вписанной в любой треугольник, равняется удвоенной площади треугольника, деленной на его периметр.
где a, b, c – стороны треугольника, S – его площадь.
Прямоугольный треугольник
Радиус окружности, вписанной в прямоугольный треугольник, равняется дроби, в числителе которого сумма катетов минус гипотенуза, в знаменателе – число 2.
где a и b – катеты, c – гипотенуза треугольника.
Равнобедренный треугольник
Радиус вписанной в равнобедренный треугольник окружности вычисляется по формуле ниже:
где a – боковые стороны, b – основание треугольника.
Равносторонний треугольник
Радиус вписанной в правильный (равносторонний) треугольник окружности рассчитывается следующим образом:
где a – сторона треугольника.
Видео:Высота равностороннего треугольника равна 13√3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Примеры задач
Задание 1
Дан треугольник со сторонами 5, 7 и 10 см. Вычислите радиус вписанной в него окружности.
Решение
Сперва вычислим площадь треугольника. Для этого применим формулу Герона:
Остается только применить соответствующую формулу для вычисления радиуса круга:
Задание 2
Боковые стороны равнобедренного треугольника равны 16 см, а основание 7 см. Найдите радиус вписанной в фигуру окружности.
Решение
Воспользуемся подходящей формулой, подставив в нее известные значения:
🎥 Видео
ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Задача 6 №27624 ЕГЭ по математике. Урок 71Скачать

Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать

Задача 6 №27921 ЕГЭ по математике. Урок 138Скачать

Задача 6 №27892 ЕГЭ по математике. Урок 126Скачать

2047 радиус окружности описанной около правильного треугольника равна 36 корней из 3Скачать

Формулы равностороннего треугольника #shortsСкачать

Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

Задание 16 ОГЭ по математике. Окружность описана около равностороннего треугольника. Задача 2Скачать

ОГЭ 16🔴Скачать

Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать