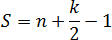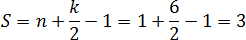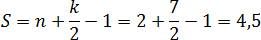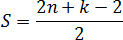Узлы сетки в окружности

Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок. Это даже не формула, а настоящая теорема. На первый взгляд, она может показаться сложной. Но достаточно решить пару задач — и вы поймете, насколько это крутая фишка. Так что вперед!

Для начала введем новое определение:

— это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки.

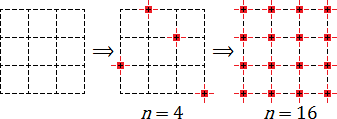
На первой картинке узлы вообще не обозначены. На второй обозначены 4 узла. Наконец, на третьей картинке обозначены все 16 узлов.

Какое отношение это имеет к задаче B5? Дело в том, что вершины многоугольника в таких задачах всегда лежат в узлах сетки. Как следствие, для них работает следующая теорема:

Теорема. Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки. Тогда площадь многоугольника равна:

где n — число узлов внутри данного многоугольника, число узлов, которые лежат на его границе (граничных узлов).

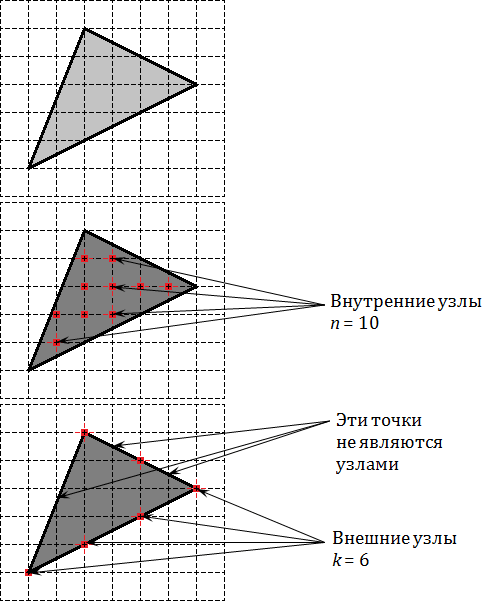
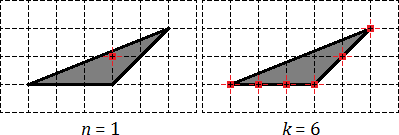
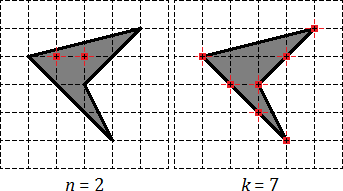
В качестве примера рассмотрим обычный треугольник на координатной сетке и попробуем отметить внутренние и граничные узлы.

На первой картинке дан обычный треугольник. На второй отмечены его внутренние узлы, число которых равно На третей картинке отмечены узлы лежащие на границе, их всего

Возможно, многим читателям непонятно, как считать числа Начните с внутренних узлов. Тут все очевидно: закрашиваем треугольник карандашом и смотрим, сколько узлов попало под закраску.

С граничными узлами чуть сложнее. Граница многоугольника — замкнутая ломаная, которая пересекает координатную сетку во многих точках. Проще всего отметить какую-нибудь «стартовую» точку, а затем обойти остальные.

Граничными узлами будут только те точки на ломаной, в которых одновременно пересекаются

1. Собственно, ломаная;
2. Горизонтальная линия координатной сетки;
3. Вертикальная линия.

Посмотрим, как все это работает в настоящих задачах.

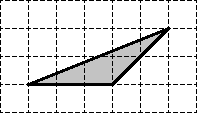
Задача. Найдите площадь треугольника, если размер клетки равен 1 x 1 см:

Для начала отметим узлы, которые лежат внутри треугольника, а также на его границе:

Получается, что внутренний узел всего один: Граничных узлов — целых шесть: три совпадают с вершинами треугольника, а еще три лежат на сторонах.

Теперь считаем площадь по формуле:

Вот и все! Задача решена.

Задача. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см. Ответ дайте в квадратных сантиметрах.

Снова отмечаем внутренние и граничные узлы. Внутренних узлов всего Граничных узлов: из которых 4 являются вершинами четырехугольника, а еще 3 лежат на сторонах.

Остается подставить числа в формулу площади:

Обратите внимание на последний пример. Эту задачу реально предлагали на диагностической работе в 2012 году. Если работать по стандартной схеме, придется делать много дополнительных построений. А методом узлов все решается практически устно.

Видео:Краткая видеоинструкция: как завязывать узлы на гладиаторской сетке.Скачать

Важное замечание по площадям

Но формула — это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю. Получим:

Числа n и k — это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт:

Площадь всегда выражается целым числом или дробью. Причем в конце дроби всегда стоит «пять десятых»: 10,5; 17,5 и т.д.

Таким образом, площадь в задаче B5 всегда выражается целым числом или дробью Если ответ получается другим, значит, где-то допущена ошибка. Помните об этом, когда будете сдавать настоящий ЕГЭ по математике!

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Задачи на координатной сетке

Видео:Радиус описанной окружностиСкачать

Задачи на координатной сетке

Площадь фигур на координатной сетке или плоскости можно решить несколькими способами:

1. Достроить фигуру до прямоугольника или квадрата.

2. Найти площадь прямоугольника.

3. Найти площади всех дополнительных фигур (чаще всего это прямоугольные треугольники или трапеции).

4. Из площади прямоугольника вычесть все площади дополнительных фигур.

Найдите площадь четырёхугольника, вершины которого имеют координаты $(0;5), (4;7), (7;0), (11;2)$.

1. Достроим параллелограмм до прямоугольника

2. Найдем длину и ширину прямоугольника:

Чтобы найти длину стороны, параллельную какой либо оси, надо из большей координаты отнять меньшую координату.

Длина стороны $EF= 11$, стороны $FK= 7$. Подставим в формулу площади данные и сделаем вычисления: $S_= 11·7=77$.

3. Найдем площади дополнительных (ненужных) фигур:

4. Из площади прямоугольника вычтем все площади дополнительных фигур и таким образом получим площадь искомого параллелограмма.

• Второй способ

1. Если линии фигуры идут ровно по клеточкам и можно посчитать длины сторон, высот и т.д., то считаем клеточки и определяем величины.

2. Подставляем известные значения в формулу площади.

• Третий способ.

Площадь искомой фигуры можно найти по формуле Пика:

$S=/+В-1$, где $Г$ — количество узлов на границе фигуры (на сторонах и вершинах);

$В$ — количество узлов внутри фигуры.

Узел – это уголок клетки или пересечение линий

Найдите площадь четырёхугольника, изображённого на клетчатой бумаге с размером клетки $1 см × 1$ см. Ответ дайте в квадратных сантиметрах.

Отметим красными точками узлы на границе фигуры (Г), а желтыми – узлы внутри фигуры (В).

Подставим данные в формулу Пика: $S=/+6-1=3.5+6-1=8.5$

Площади некоторых фигур

Площадь треугольника:

1. $S=/$, где $h_a$ — высота, проведенная к стороне $а$
2. Для прямоугольного треугольника $S=/$, где $а$ и $b$ — катеты прямоугольного треугольника.
3. Для равностороннего треугольника $S=<a^√3>/$, где $а$ — длина стороны.

Площади четырехугольников:

1. Прямоугольник $S=a·b$, где $а$ и $b$ — смежные стороны.
2. Ромб $S=/$, где $d_1$ и $d_2$ — диагонали ромба
3. Трапеция $S=/$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
4. Квадрат $S=a^2$, где $а$ — сторона квадрата.
5. Параллелограмм $S=a·h_a$, где $h_a$ — высота, проведенная к стороне $а$.

Площадь круга:

$S=π·R^2$, где $π=3.14, R$ — радиус окружности.

Площадь сектора:

$S=<S_n°>/=/$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Площадь кольца:

В прямоугольнике и квадрате центр описанной окружности лежит в точке пересечения диагоналей, а радиус описанной окружности равен половине диагонали.

В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы и радиус равен половине гипотенузы.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

В прямоугольном треугольнике $АВС$ для острого угла $В$:

Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

$cos BOA= — cos BOC$;

$ctg BOA= — ctg BOC$.

Углы в окружности.

1. Угол, образованный двумя радиусами, называется центральным. Центральный угол равен градусной мере дуги, на которую он опирается.

2. Угол, вершина которого лежит на окружности, а стороны являются хордами, называется вписанным. Вписанный угол равен половине градусной меры дуги, на которую он опирается

Найдите величину угла MPK. Ответ дайте в градусах.

Угол $МРК$ равен половине градусной меры дуги $МК$, так как он вписанный. Чтобы отыскать градусную меру дуги, посмотрим, на сколько таких дуг мы можем разделить всю окружность, потом $360°$ разделим на полученное количество.

Дуга $МК$ отсекается хордой, занимающей две клетки. Разделим такими хордами всю окружность, получилось $8$ дуг.

$360:8=45°$, составляет градусная мера дуги $МК$.

Прямые на координатной плоскости

Координаты середины отрезка равны среднему арифметическому координат его концов.

Найдите абсциссу середины отрезка, соединяющего точки $В(2;8)$ и $A(6;4)$.

Пусть точка $М$ – середина отрезка $ВА$. Чтобы найти абсциссу данной точки, надо найти среднее арифметическое абсцисс концов отрезка:

Уравнение прямой, проходящей через две заданные точки на плоскости имеет вид $y=kx+b$, где $k$ и $b$ – это коэффициенты.

Уравнение можно задать с помощью формулы:

Точки пересечения прямой с осями координат:

Если прямая пересекает ось Ох, то в уравнении прямой координата $у = 0$, а если прямая пересекает ось Оу, то уравнении прямой координата $х = 0$.

Две прямые на координатной плоскости будут параллельны, если в уравнениях прямых будут равны коэффициенты k.

Если уравнение первой прямой: $y=k_x+b_1$;

Уравнение второй прямой: $y= k_x+b_2$, то при параллельности прямых, $k_1=k_2$.

Видео:ТОП 10 УЗЛОВ для ПОВСЕДНЕВНОЙ ЖИЗНИСкачать

Окружности на клетчатой бумаге

Видео:Все об окружностях на ЕГЭ | Профильная математика 2023 | УмскулСкачать

Задача

а) Постройте окружность, проходящую ровно через 12 узлов клетчатой бумаги.
б) Постройте окружность, проходящую ровно через 6 узлов клетчатой бумаги.
в) Постройте окружность, проходящую ровно через 5 узлов клетчатой бумаги.

Видео:Узлы для вязания сетей.Скачать

Подсказка 1

Обратите внимание, что если центр окружности сам является узлом клетчатой бумаги, то количество лежащих на этой окружности узлов кратно четырём. Если же центр окружности находится в середине стороны какой-либо клеточки, то на такой окружности будет расположено чётное число узлов. Это относится и к тем случаям, когда окружность вообще не проходит через узлы клетчатой бумаги, потому что ноль делится как на 2, так и на 4 (и вообще на любое натуральное число).

Видео:Окружности №1 в ЕГЭ | Профильная математика ЕГЭ 2024 | УмскулСкачать

Подсказка 2

Будем считать, что расстояние между соседними узлами клетчатой бумаги равно единице. Тогда на ней можно задать систему координат таким образом, чтобы множество всех узлов в точности совпадало со множеством всех точек, обе координаты которых целочисленны.

а) Воспользуйтесь тем фактом, что если центр окружности радиуса r является началом координат, то количество лежащих на ней узлов клетчатой бумаги есть число целочисленных решений уравнения

б) Если r 2 — нечётное целое число, то в каждой паре вида (x, y), являющейся решением уравнения (1), одно из чисел чётное, а другое — нечётное, причём количество пар, в которых первое число нечётное, равно количеству пар, в которых второе число нечётное.

в) В качестве центра такой окружности можно выбрать точку (1/3, 0).

Видео:ТОП-3 конструкции с окружностями для №16 из ЕГЭ 2023 по математикеСкачать

Подсказка 3

Попробуйте изучить окружности, квадраты радиусов которых имеют вид 5 k , 5 k /4 и 5 k /9 соответственно.

Видео:Вязание верёвочной лестницыСкачать

Решение

а) Рассмотрим уравнение

Его решениями являются двенадцать пар чисел вида (±5, 0), (0, ±5), (±3, ±4) и (±4, ±3). Нетрудно убедиться простым перебором, что других целочисленных решений данное уравнение не имеет. Следовательно, на окружности радиуса 5 с центром в начале координат лежит ровно 12 узлов клетчатой бумаги (рис. 1).

б) Пусть центр окружности радиуса 5/2 расположен в точке (1/2, 0). Тогда эта окружность задаётся уравнением

Домножая обе части равенства на 4, можно перейти к такому соотношению:

Если же сделать переобозначения вида a = (2x – 1) и b = 2y, то мы придём к уравнению вида a 2 + b 2 = 25. Оно, как мы знаем из пункта а), имеет в точности 12 целочисленных решений (потому что это решения уравнения (2)), причём ровно в половине из них число a нечётное, а число b — чётное. Значит, уравнение (3) обладает в точности шестью целочисленными решениями. А именно, ему удовлетворяют следующие пары чисел: (3, 0), (–2, 0), (2, ±2) и (–1, ±2). Таким образом, на окружности радиуса 5/2 с центром в точке (1/2, 0) лежит ровно 6 узлов клетчатой бумаги (рис. 2).

в) Внимательный читатель наверняка заметил, что решение пункта б), по существу, вытекало из пункта а). Более того, можно было рассмотреть задачу в более общем виде и доказать такое утверждение: если на окружности радиуса r, центр которой находится в начале координат, лежит 4n узлов клетчатой бумаги и число r 2 — нечётное, то на окружности радиуса r/2 с центром в точке (1/2, 0) расположено 2n узлов. Ниже на примере нашей задачи мы покажем, как подобным методом получить окружность, на которой лежит ровно n узлов.

Для начала рассмотрим окружность с центром в начале координат, радиус которой равен 25. Эта окружность задаётся уравнением

которому, как нетрудно проверить, удовлетворяют двадцать пар целочисленных решений: (±25, 0), (0, ±25), (±7, ±24), (±24, ±7), (±15, ±20) и (±20, ±15). То есть на этой окружности находится ровно 20 узлов клетчатой бумаги.

Теперь рассмотрим окружность радиуса 25/3, центром которой является точка (1/3, 0). Задающее её уравнение имеет вид

что после соответствующих преобразований превращается в соотношение

Как и в пункте б), сделав замену a = (3x – 1), b = 3y, мы получим уравнение a 2 + b 2 = 625, решения которого нам известны. Осталось понять, какие из них нам подходят, а какие — нет. Но это оказывается довольно просто: если c делится на 3, то из каждой четвёрки решений вида (c, d), (c, –d), (d, c), (–d, c) подходит ровно одно. В нашем случае, это (–8, 0), (–2, ±8), (7, ±5). И таким образом, на окружности, которая задана уравнением (5), лежит ровно 5 узлов клетчатой бумаги (рис. 3).

Замечание. Глядя на пять красных точек, изображённых на рис. 3, читатель может подумать, что если последовательно соединить их друг с другом, получится правильный пятиугольник. Однако это не так: у этого пятиугольника между собой равны только три стороны, а две другие немножко меньше. В действительности на клетчатой бумаге расположить правильный пятиугольник нельзя. Как и любой другой правильный многоугольник, за исключением квадрата.

Видео:#13. Задача с параметром: уравнение окружности!Скачать

Послесловие

Придумав решение самостоятельно или ознакомившись с изложенным выше, читатель, наверное, задастся таким вопросом: правда ли, что какое натуральное число n мы ни возьмём, найдётся такая окружность, на которой лежит ровно n узлов клетчатой бумаги? Оказывается, это действительно так, причём методы построения этих окружностей не слишком отличаются от тех, которые мы уже видели. Вкратце изложим суть дела.

Ключевым моментом решения проблемы является следующая лемма.

Лемма. Уравнение x 2 + y 2 = 5 k имеет ровно 4(k + 1) целочисленных решений для любого целого неотрицательного k.

(На самом деле представленная лемма является частным случаем более общего факта. Именно, пусть r(n) обозначает число всевозможных способов представления натурального n в виде суммы квадратов пары целых чисел. Тогда можно доказать, что r(n) = d₁(n) – d₃(n), где d₁(n) и d₃(n) — числа, отвечающие количеству делителей n вида (4k + 1) и (4k + 3) соответственно.)

Для доказательства мы проверяем сначала, что утверждение леммы справедливо при k = 0 и k = 1. В самом деле, уравнение x 2 + y 2 = 1 имеет четыре целочисленных решения: (0, ±1) и (±1, 0). А уравнение x 2 + y 2 = 5 обладает ровно восемью корнями: (±2, ±1) и (±1, ±2).

Потом в дело вступает принцип математической индукции. С его помощью можно доказать, что при всех целых k > 1 уравнение x 2 + y 2 = 5 k имеет ровно восемь таких решений (x, y), что x и y не делятся на 5. Точно так же, как и корни уравнения x 2 + y 2 = 5, эти восемь пар чисел получаются друг из друга перестановкой x и y и изменениями знаков. А вместе с 4(k – 1) парами вида (5a, 5b), где (a, b) — решения уравнения a 2 + b 2 = 5 k –2 , они дают нам в точности 4(k + 1) решений исходного уравнения.

Теперь, вооружившись леммой, мы легко сможем дать ответ на поставленный вопрос. Из соображений симметрии ясно, что если расположить центр окружности в узле клетчатой бумаги (например, в начале координат), то количество лежащих на ней узлов будет делиться на четыре. А из леммы сразу вытекает, что если квадрат радиуса такой окружности равен 5 k , то на этой окружности лежит ровно 4(k + 1) узлов. В частности, на окружности x 2 + y 2 = 25 расположено ровно 12 узлов клетчатой бумаги.

В качестве примера окружности, на которой лежит произвольное наперёд заданное чётное число узлов клетчатой бумаги, мы можем взять окружность, заданную уравнением:

(6)

Чтобы убедиться в том, что она годится (то есть что на ней лежит 2(k + 1) узлов), достаточно повторить рассуждения из решения пункта б) и применить лемму. Если же хочется провести окружность через нечётное число узлов, то можно взять такую:

(7)

Используя лемму и свойства делимости на 3, можно доказать, что на ней лежит ровно (2k + 1) узлов, а выбирая подходящее k, это количество можно сделать любым наперёд заданным нечётным числом.

Окружности, которые задаются уравнениями (6) и (7), называются окружностями Шинцеля, по имени польского математика Анджея Шинцеля (Andrzej Schinzel). Отметим, что для данного натурального числа n эти уравнения задают, вообще говоря, не самую маленькую окружность с n узлами клетчатой бумаги на ней. Например, так происходит с n = 1 (очевидно, можно предъявить окружность сколь угодно маленького радиуса) или с n = 4 (здесь ясно, что существует окружность радиуса 1/√2. Менее тривиальный пример: n = 9. Соответствующая окружность Шинцеля имеет радиус 625/3, однако на окружности с центром (1/3, 0) и радиусом 65/3 также лежит ровно 9 узлов клетчатой бумаги.

Существуют также и менее тривиальные комбинации точек. Так, на рис. 4 изображена окружность с центром в точке (1/5, 2/5) и радиусом — на ней лежат четыре узла клетчатой бумаги: (–6, –2), (1, 7), (5, 5) и (2, –6). А на окружности с центром в точке (1/7, 2/7) и радиусом находятся пять узлов: , , , и (рис. 5).

Описание множества окружностей, которые проходят ровно через n узлов клетчатой бумаги для заданного натурального числа n, — пока нерешённая задача. Предполагается, что окружность, проходящая более чем через три узла, — достаточно редкое явление, то есть если провести окружность через три случайно выбранных узла клетчатой бумаги, то через четвёртый она пройдёт с малой вероятностью.

С этой задачей также связан вопрос об изображении круга на экране монитора. Будем считать, что экран представляет собой прямоугольный лист клетчатой бумаги, а круг на экране — объединение тех клеточек (пикселей), которые пересекаются со внутренностью круга. Тогда вопрос заключается в том, сколько различных изображений на экране имеет круг данного радиуса. Например, на рис. 6 представлено три различных изображения круга радиуса 4/5 (сторона клеточки, соответственно, равна единице). Полного ответа на этот вопрос пока тоже нет.

При подготовке данной публикации использовалась статья В. Вавилова и А. Устинова Окружности на решетках («Квант» №6, 2006), в которой обсуждаются некоторые свойства целочисленных решеток и расположение окружностей на них.

📽️ Видео

Как вязать узлы на гладиаторской сеткеСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Гимнастические кольца к ДСК «Пионер»: как завязать узелСкачать

ЕГЭ по математике: задание 18 (C5) про две окружности и модульСкачать

Задача B3: площадь закрашенного сектораСкачать

#17. Плавающий центр окружности — красивая задача с параметром!Скачать

СЕТКА, ЛИНЕЙКИ, НАПРАВЛЯЮЩИЕ. СЕКРЕТЫ ИСПОЛЬЗОВАНИЯ. Corel DRAW. КОРЕЛ. Уроки для начинающихСкачать

Взаимное расположение окружности и прямой. 7 класс.Скачать

ИЗИ Егэ. Планиметрия задания 3 и 6 из профильного ЕГЭ по математике: решаем прототипыСкачать

Как правильно плести сеть для раколовки (подсака, садка) по кругуСкачать