Все формулы по геометрии за 8 класс окружность

Определения

Центральный угол – это угол, вершина которого лежит в центре окружности.

Вписанный угол – это угол, вершина которого лежит на окружности.

Градусная мера дуги окружности – это градусная мера центрального угла, который на неё опирается.

Теорема

Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.

Доказательство

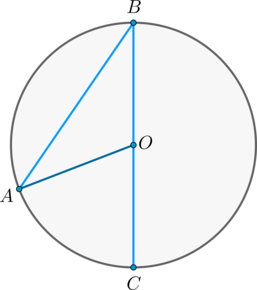
Доказательство проведём в два этапа: сначала докажем справедливость утверждения для случая, когда одна из сторон вписанного угла содержит диаметр. Пусть точка (B) – вершина вписанного угла (ABC) и (BC) – диаметр окружности:

Треугольник (AOB) – равнобедренный, (AO = OB) , (angle AOC) – внешний, тогда (angle AOC = angle OAB + angle ABO = 2angle ABC) , откуда (angle ABC = 0,5cdotangle AOC = 0,5cdotbuildrelsmileover) .

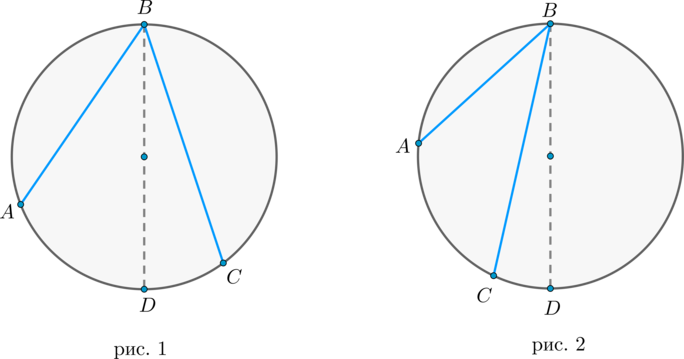
Теперь рассмотрим произвольный вписанный угол (ABC) . Проведём диаметр окружности (BD) из вершины вписанного угла. Возможны два случая:

1) диаметр разрезал угол на два угла (angle ABD, angle CBD) (для каждого из которых теорема верна по доказанному выше, следовательно верна и для исходного угла, который является суммой этих двух и значит равен полусумме дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 1.

2) диаметр не разрезал угол на два угла, тогда у нас появляется ещё два новых вписанных угла (angle ABD, angle CBD) , у которых сторона содержит диаметр, следовательно, для них теорема верна, тогда верна и для исходного угла (который равен разности этих двух углов, значит, равен полуразности дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 2.

Следствия

1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.

2. Вписанный угол, опирающийся на полуокружность, прямой.

3. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.

Определения

Существует три типа взаимного расположения прямой и окружности:

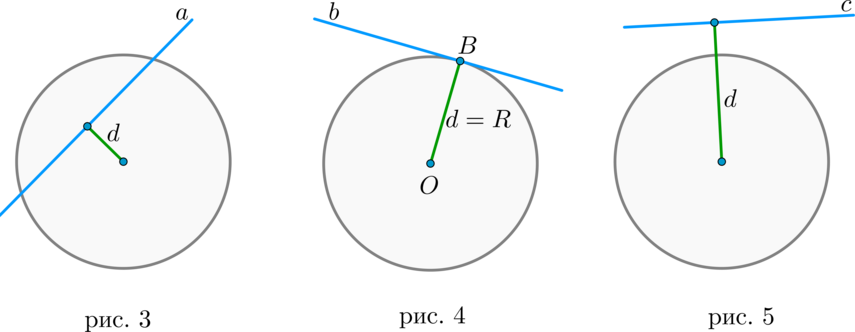
1) прямая (a) пересекает окружность в двух точках. Такая прямая называется секущей. В этом случае расстояние (d) от центра окружности до прямой меньше радиуса (R) окружности (рис. 3).

2) прямая (b) пересекает окружность в одной точке. Такая прямая называется касательной, а их общая точка (B) – точкой касания. В этом случае (d=R) (рис. 4).

3) прямая (c) не имеет общих точек с окружностью (рис. 5).

Теорема

1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

2. Если прямая проходит через конец радиуса окружности и перпендикулярна этому радиусу, то она является касательной к окружности.

Следствие

Отрезки касательных, проведенных из одной точки к окружности, равны.

Доказательство

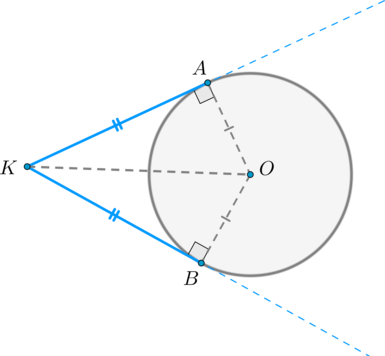
Проведем к окружности из точки (K) две касательные (KA) и (KB) :

Значит, (OAperp KA, OBperp KB) как радиусы. Прямоугольные треугольники (triangle KAO) и (triangle KBO) равны по катету и гипотенузе, следовательно, (KA=KB) .

Следствие

Центр окружности (O) лежит на биссектрисе угла (AKB) , образованного двумя касательными, проведенными из одной точки (K) .

Теорема об угле между секущими

Угол между двумя секущими, проведенными из одной точки, равен полуразности градусных мер большей и меньшей высекаемых ими дуг.

Доказательство

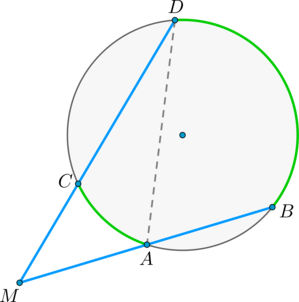
Пусть (M) – точка, из которой проведены две секущие как показано на рисунке:

Покажем, что (angle DMB = dfrac(buildrelsmileover — buildrelsmileover)) .

(angle DAB) – внешний угол треугольника (MAD) , тогда (angle DAB = angle DMB + angle MDA) , откуда (angle DMB = angle DAB — angle MDA) , но углы (angle DAB) и (angle MDA) – вписанные, тогда (angle DMB = angle DAB — angle MDA = fracbuildrelsmileover — fracbuildrelsmileover = frac(buildrelsmileover — buildrelsmileover)) , что и требовалось доказать.

Теорема об угле между пересекающимися хордами

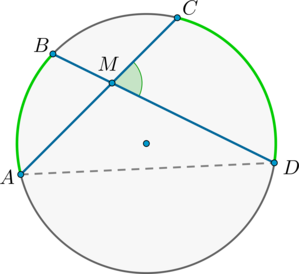
Угол между двумя пересекающимися хордами равен полусумме градусных мер высекаемых ими дуг: [angle CMD=dfrac12left(buildrelsmileover+buildrelsmileoverright)]

Доказательство

(angle BMA = angle CMD) как вертикальные.

Из треугольника (AMD) : (angle AMD = 180^circ — angle BDA — angle CAD = 180^circ — frac12buildrelsmileover — frac12buildrelsmileover) .

Но (angle AMD = 180^circ — angle CMD) , откуда заключаем, что [angle CMD = frac12cdotbuildrelsmileover + frac12cdotbuildrelsmileover = frac12(buildrelsmileover + buildrelsmileover).]

Теорема об угле между хордой и касательной

Угол между касательной и хордой, проходящей через точку касания, равен половине градусной меры дуги, стягиваемой хордой.

Доказательство

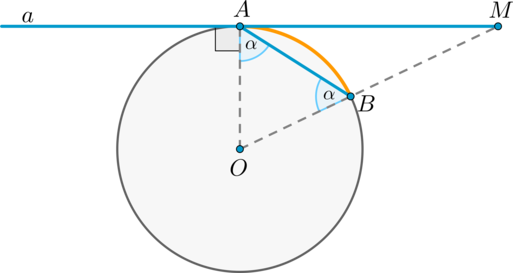
Пусть прямая (a) касается окружности в точке (A) , (AB) – хорда этой окружности, (O) – её центр. Пусть прямая, содержащая (OB) , пересекает (a) в точке (M) . Докажем, что (angle BAM = frac12cdot buildrelsmileover) .

Обозначим (angle OAB = alpha) . Так как (OA) и (OB) – радиусы, то (OA = OB) и (angle OBA = angle OAB = alpha) . Таким образом, (buildrelsmileover = angle AOB = 180^circ — 2alpha = 2(90^circ — alpha)) .

Так как (OA) – радиус, проведённый в точку касания, то (OAperp a) , то есть (angle OAM = 90^circ) , следовательно, (angle BAM = 90^circ — angle OAB = 90^circ — alpha = frac12cdotbuildrelsmileover) .

Теорема о дугах, стягиваемых равными хордами

Равные хорды стягивают равные дуги, меньшие полуокружности.

И наоборот: равные дуги стягиваются равными хордами.

Доказательство

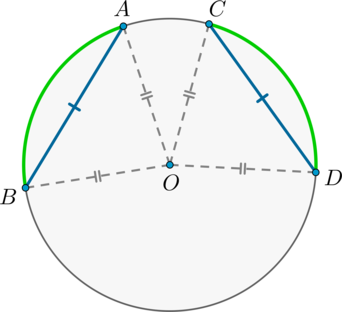
1) Пусть (AB=CD) . Докажем, что меньшие полуокружности дуги (buildrelsmileover=buildrelsmileover) .

(triangle AOB=triangle COD) по трем сторонам, следовательно, (angle AOB=angle COD) . Но т.к. (angle AOB, angle COD) — центральные углы, опирающиеся на дуги (buildrelsmileover, buildrelsmileover) соответственно, то (buildrelsmileover=buildrelsmileover) .

2) Если (buildrelsmileover=buildrelsmileover) , то (triangle AOB=triangle COD) по двум сторонам (AO=BO=CO=DO) и углу между ними (angle AOB=angle COD) . Следовательно, и (AB=CD) .

Теорема

Если радиус делит хорду пополам, то он ей перпендикулярен.

Верно и обратное: если радиус перпендикулярен хорде, то точкой пересечения он делит ее пополам.

Доказательство

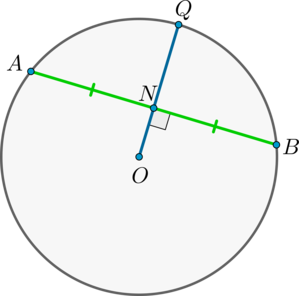
1) Пусть (AN=NB) . Докажем, что (OQperp AB) .

Рассмотрим (triangle AOB) : он равнобедренный, т.к. (OA=OB) – радиусы окружности. Т.к. (ON) – медиана, проведенная к основанию, то она также является и высотой, следовательно, (ONperp AB) .

2) Пусть (OQperp AB) . Докажем, что (AN=NB) .

Аналогично (triangle AOB) – равнобедренный, (ON) – высота, следовательно, (ON) – медиана. Следовательно, (AN=NB) .

Теорема о произведении отрезков хорд

Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

Доказательство

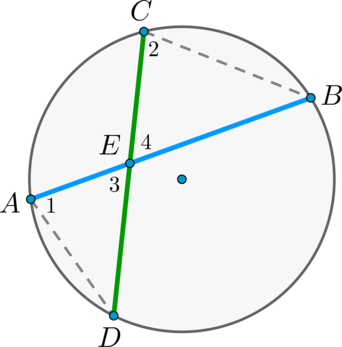
Пусть хорды (AB) и (CD) пересекаются в точке (E) .

Рассмотрим треугольники (ADE) и (CBE) . В этих треугольниках углы (1) и (2) равны, так как они вписанные и опираются на одну и ту же дугу (BD) , а углы (3) и (4) равны как вертикальные. Треугольники (ADE) и (CBE) подобны (по первому признаку подобия треугольников).

Тогда (dfrac = dfrac) , откуда (AEcdot BE = CEcdot DE) .

Теорема о касательной и секущей

Квадрат отрезка касательной равен произведению секущей на ее внешнюю часть.

Доказательство

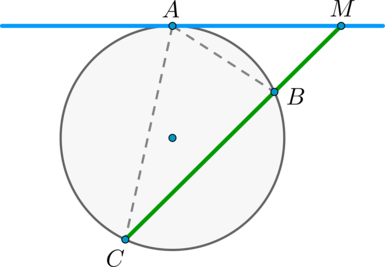
Пусть касательная проходит через точку (M) и касается окружности в точке (A) . Пусть секущая проходит через точку (M) и пересекает окружность в точках (B) и (C) так что (MB . Покажем, что (MBcdot MC = MA^2) .

Рассмотрим треугольники (MBA) и (MCA) : (angle M) – общий, (angle BCA = 0,5cdotbuildrelsmileover) . По теореме об угле между касательной и секущей, (angle BAM = 0,5cdotbuildrelsmileover = angle BCA) . Таким образом, треугольники (MBA) и (MCA) подобны по двум углам.

Из подобия треугольников (MBA) и (MCA) имеем: (dfrac = dfrac) , что равносильно (MBcdot MC = MA^2) .

Следствие

Произведение секущей, проведённой из точки (O) , на её внешнюю часть не зависит от выбора секущей, проведённой из точки (O) :

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Плоские геометрические фигуры: свойства и основные формулы

В статье описываются геометрические фигуры: определение, основные свойства и формулы.

Плоские геометрические фигуры:

Четырехугольник (общее для всех четырехугольников)

Квадрат

Прямоугольник

Параллелограмм

Трапеция

Треугольник

Окружность

Геометрические фигуры — это любое сочетание точек, линий и поверхностей. Геометрические фигуры разделяются на плоские и объемные.

Плоские геометрические фигуры — это фигуры, все точки которых лежат на одной плоскости. Объемные геометрические фигуры — это фигуры, не все точки которых лежат на одной плоскости.

Видео:ВСЯ ГЕОМЕТРИЯ 8 КЛАСС ЗА 15 МИНУТ / АТАНАСЯН / К ОГЭСкачать

Четырёхугольник

Четырёхугольник – это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Основные свойства:

• Сумма углов четырёхугольника равна 360°
• Не существует четырёхугольников, у которых все углы острые или все углы тупые.
• Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
• Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.

В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Видео:Вся геометрия 8 класса с нуля для ОГЭ по математике 2024Скачать

Квадрат

Квадрат – правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Основные формулы:

Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a 2 или S=d 2 /2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
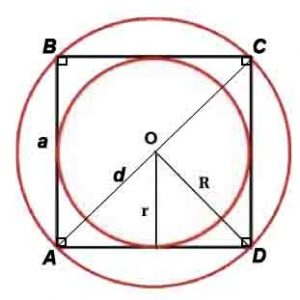
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2

где a-сторона, d-диагональ, P-периметр, S-площадь
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.

Свойства:

• Все стороны равны, все углы равны и составляют 90°;
• Диагонали квадрата равны и перпендикулярны;
• У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
• Квадрат является одновременно частным случаем ромба и прямоугольника.

Видео:ВСЯ ГЕОМЕТРИЯ ИЗ ОГЭ ПО МАТЕМАТИКЕ 2023 ЗА 40 МИНУТСкачать

Прямоугольник

Прямоугольник – четырехугольник, у которого все углы прямые.

Основные формулы:

Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S = d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a 2 +b 2 )/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a 2 +b 2 )/2 (теорема Пифагора)

где a, b – длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
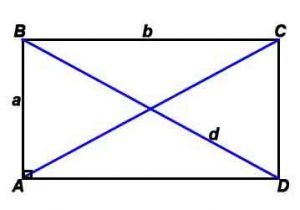
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a 2 +b 2 ) – корень квадратный из (a 2 +b 2 ).

Свойства:

• Диагонали прямоугольника равны и делятся точкой пересечения пополам.
• Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.

Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Параллелограмм

Параллелограмм – четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Определения:

Высота параллелограмма – это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.

Основные формулы:

Стороны и диагональ связаны соотношением: (d₁) 2 +(d₂) 2 =(a 2 +b 2 )*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте: S = a*h
S (Площадь) по двум сторонам и углу между ними: S=a*b*sin α
S (Площадь) по двум диагоналям и углу между ними: S=(d₁*d₂)/2*sin γ

где a, b – длины сторон, d₁, d₂ –диагонали, P-периметр, S-площадь,
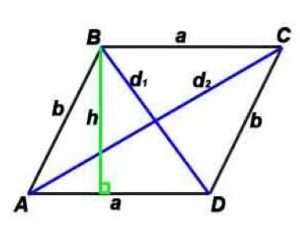
h-высота, проведенная к противоположной стороне
α – угол между сторонами параллелограмма,
γ – угол между диагоналями параллелограмма (острый).

Свойства:

• У параллелограмма противоположные стороны равны и противоположные углы равны.
• Сумма любых двух соседних углов параллелограмма равна 180°.
• Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
• Каждая диагональ делит параллелограмм на два равных треугольника.
• Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
• Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
• Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Видео:Вся геометрия 7–9 класс с нуля | ОГЭ МАТЕМАТИКА 2023Скачать

Ромб

Ромб – это параллелограмм, у которого все стороны равны.

Основные формулы:

Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d₁*d₂)/2
Радиус окружности, вписанной в ромб: r=h/2 или r =(d₁*d₂)/4a
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a 2 · sin α

где a – длина стороны, d₁, d₂ –диагонали, P-периметр, S-площадь,
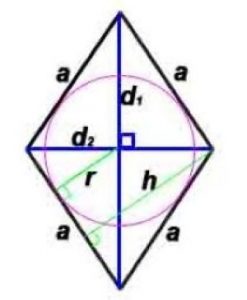
h -высота, проведенная к противоположной стороне
α – угол между сторонами ромба

Свойства:

• Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
• В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d₁*d₂/4a.

Видео:Геометрия 8 класс за 1 час | Математика | УмскулСкачать

Трапеция

Трапеция – четырёхугольник, у которого только две противолежащие стороны параллельны.

Определения:

• Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
• Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
• Средняя линия (первая средняя линия) трапеции – отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
• Средняя линия (вторая средняя линия) – отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
• Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
• Прямоугольная трапеция – трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.

Основные формулы:

Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2

где a,b – основания, c,d – боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d₁, d₂ –диагонали,
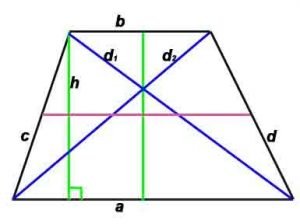
P-периметр, S-площадь, h -высота, проведенная к противоположной стороне

Свойства:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.

Видео:ВСЯ ТЕОРИЯ по ГЕОМЕТРИИ ЗА 8 КЛАСС с примерамиСкачать

Треугольник

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Определения:

• Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
• Высота треугольника – перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
• Медиана треугольника– отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
• Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
• Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
• Равнобедренный треугольник– треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
• Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
• Прямоугольный треугольник – треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.

Основные формулы:

Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь: по сторонам и углу между ними: S=(a*b)/2* sin γ
по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c 2 =a 2 +b 2 (Теорема Пифагора)

где a,b, c – стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
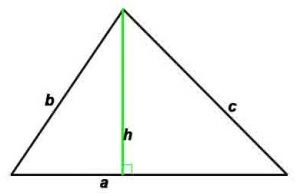
d₁, d₂ –диагонали, h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ – угол между сторонами a и b
r – радиус вписанной окружности, R – радиус описанной окружности

Свойства:

• В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
• Сумма углов треугольника равна 180°:
• Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b| 2 =a 2 +b 2 (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.

Видео:КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

Окружность

Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Определения:

• Радиус – отрезок, который соединяет центр окружности с любой её точкой.
• Хорда – отрезок, который соединяет какие-либо две точки окружности (AB).
• Диаметр – хорда, проходящая через центр окружности(d). Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует.
• Касательная – прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
• Секущая – прямая, которая пересекает окружность в двух различных точках.

Основные формулы:

Длина окружности: L = 2πR
Площадь круга: S = π*r 2 или S = π*d 2 /4

где π = 3,14 (3,1415926535) – величина постоянная,
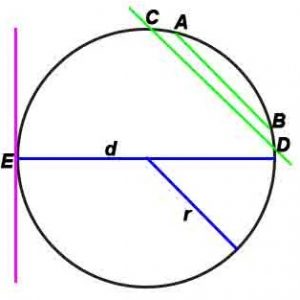
где r-радиус, d –диаметр, L – длина окружности, S-площадь.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Геометрия. Урок 5. Окружность

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Определение окружности

• Отрезки в окружности

Видео:Хитрости в решении геометрических задач в ОГЭ по математике | Математика TutorOnlineСкачать

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Эта точка называется центром окружности .

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Отрезки в окружности

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Видео:ВСЯ ГЕОМЕТРИЯ ЗА 30 МИНУТСкачать

Дуга в окружности

Часть окружности, заключенная между двумя точками, называется дугой окружности .

Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .

Теорема 4:
Равные хорды стягивают равные дуги.

Если A B = C D , то ∪ A B = ∪ C D

Видео:Площади фигур. Сохраняй и запоминай!#shortsСкачать

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Градусная мара всей окружности равна 360 ° .

Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ A C B – вписанный.

Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α

Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Видео:ВСЯ ГЕОМЕТРИЯ 9 класса в одной задаче | Математика | TutorOnlineСкачать

Длина окружности, длина дуги

Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .

Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

Длина дуги окружности , на которую опирается центральный угол α равна:

l α = π R 180 ∘ ⋅ α

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Видео:Всё об окружностях для ОГЭ🔥🔥🔥Скачать

Теорема синусов

Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.

🔥 Видео

Основы геометрии #геометрия #окружность #радиус #8классСкачать

Математика| Геометрия 8 класса в одной задачеСкачать