Коэффициент подобия треугольников cos (3 видео)

Коэффициент подобия треугольников cos

Признака подобия треугольников

Две фигуры `F` и `F’` называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры `F` и `F’` подобны, то пишется `F

F’`. Напомним, что запись подобия треугольников `Delta ABC

Delta A_1 B_1 C_1` означает, что вершины, совмещаемые преобразованием подобия, стоят на соответствующих местах, т. е. `A` переходит в `A_1`, `B` — в `B_1`, `C` — в `C_1`.

Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если `Delta ABC

Delta A_1B_1C_1`, то `/_ A = /_ A_1`, `/_ B = /_ B_1`, `/_ C = /_ C_1`,

`A_1B_1 : AB = B_1C_1 : BC = C_1A_1 : CA`.

Два треугольника подобны, если:

1. два угла одного соответственно равны двум углам другого;

2. две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;

3. три стороны одного треугольника пропорциональны трём сторонам другого.

В решении задач и доказательстве теорем часто используется утверждение, которое, чтобы не повторять каждый раз, докажем сейчас отдельно.

Если две стороны треугольника пересекает прямая, параллельная третьей стороне (рис. 9), то она отсекает треугольник, подобный данному.

Действительно, из параллельности `MN` и `AC` следует, что углы `1` и `2` равны. Треугольники `ABC` и `MBN` имеют два равных угла: общий угол при вершине `B` и равные углы `1` и `2`. По первому признаку эти треугольники подобны.

И сразу применим это утверждение в следующем примере, в котором устанавливается важное свойство трапеции.

Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках `M` и `N`. Найти длину отрезка `MN`, если основания трапеции равны `a` и `b`.

1. Пусть `O` — точка пересечения диагоналей, `AD = a`, `BC = b`. Прямая `MN` параллельна основанию `AD` (рис. 10а), следовательно, $$ MOparallel AD$$, треугольники `BMO` и `BAD` подобны, поэтому

2. $$ ADparallel BC$$, `Delta AOD

Delta COB` по двум углам (рис. 10б):

`(OD)/(OB) = (AD)/(BC)`, то есть `(OD)/(OB) = a/b`.

3. Учитывая, что `BD = BO + OD` находим отношение

`(BO)/(BD) = (BO)/(BO + OD) = 1/(1 + OD//BO) = b/(a + b)`.

Подставляя это в (1), получаем `MO = (ab)/(a + b)`; аналогично устанавливаем, что `ON = (ab)/(a + b)`, таким образом `MN = (2ab)/(a + b)`.

Точки `M` и `N` лежат на боковых сторонах `AB` и `CD` трапеции `ABCD` и $$ MNparallel AD$$ (рис. 11а). Найти длину `MN`, если `BC = a`, `AD = 5a`, `AM : MB = 1:3`.

1. Пусть $$ BFVert CD$$ и $$ MEVert CD$$ (рис. 11б), тогда `/_ 1 = /_ 2`, `/_ 3 = /_ 4` (как соответствующие углы при пересечении двух параллельных прямых третьей) и `Delta AME

Delta MBF`. Из подобия следует `(AE)/(MF) = (AM)/(MB) = 1/3`.

2. Обозначим `MN = x`. По построению `BCNF` и `MNDE` — параллелограммы, `FN = a`, `ED = x` и, значит, `MF = x — a`; `AE = 5a — x`. Итак, имеем `(5a — x)/(x — a) = 1/3`, откуда находим `x = 4a`.

Напомним, что отношение периметров подобных треугольников равно отношению их сходственных сторон. Верно также следующее утверждение: отношение медиан, биссектрис и высот, проведённых к сходственным сторонам в подобных треугольниках, равно отношению сходственных сторон.

Отношение радиусов вписанных окружностей, как и отношение радиусов описанных окружностей, в подобных треугольниках также равно отношению сходственных сторон.

Попытайтесь доказать это самостоятельно.

Прямоугольные треугольники подобны, если:

1. они имеют по равному острому углу;

2. катеты одного треугольника пропорциональны катетам другого;

3. гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого.

Два первых признака следуют из первого и второго признаков подобия треугольников, поскольку прямые углы равны. Третий признак следует, например, из второго признака подобия и теоремы Пифагора.

Заметим, что высота прямоугольного треугольника, опущенная на гипотенузу, разбивает его на два прямоугольных треугольника, подобных между собой и подобных данному. Доказанные в § 1 метрические соотношения Свойств 1, 2, 3 можно доказать, используя подобие указанных треугольников.

СВОЙСТВА ВЫСОТ И БИССЕКТРИС

Если в треугольнике `ABC` нет прямого угла, `A A_1` и `BB_1` — его высоты, то `Delta A_1B_1C

Delta ABC` (этот факт можно сформулировать так: если соединить основания двух высот, то образуется треугольник, подобный данному).

Как всегда, полагаем `AB = c`, `BC = a`, `AC = b`.
а) Треугольник `ABC` остроугольный (рис. 12а).

В треугольнике `A A_1C` угол `A_1` — прямой, `A_1C = AC cos C = ul (b cos C)`.

В треугольнике `B B_1C` угол `B_1` — прямой, `B_1C = BC cos C = ul (a cos C)`.

В треугольниках `A_1 B_1C` и `ABC` угол `C` общий, прилежащие стороны пропорциональны: `(A_1C)/(AC) = (B_1C)/(BC) = cos C`.

Таким образом, `Delta A_1 B_1 C

Delta ABC` с коэффициентом подобия `ul (cos C)`. (Заметим, что `/_ A_1 B_1 C = /_B`).
б) Треугольник `ABC` — тупоугольный (рис. 12б), угол `C` — острый, высота `A A_1` проведена из вершины тупого угла.

$$left.begin
Delta AA_1C, angle A_1 =90^circ Rightarrow A_1C=ACcdot cos C =b cos C;\
Delta BB_1C, angle B_1 =90^circ Rightarrow B_1C=BCcdot cos C =a cos C,
end
right>Rightarrow Delta A_1B_1Csim Delta ABC,$$

коэффициент подобия `ul (cos C)`, `/_ A_1 B_1 C = /_B`.

Случай, когда угол `B` тупой, рассматривается аналогично.
в) Треугольник `ABC` — тупоугольный (рис. 12в), угол `C` — тупой, высоты `A A_1` и `B B_1` проведены из вершин острых углов.

`varphi = /_ BCB_1 = /_ ACA_1 = 180^@ — /_ C`, `cos varphi = — cos C = |cos C|`.

$$left.begin
Delta AA_1C, angle A_1 =90^circ Rightarrow A_1C=ACcdot cosvarphi =b |cos C|;\
Delta BB_1C, angle B_1 =90^circ Rightarrow B_1C=BCcdot cosvarphi =b |cos C|,
end
right>Rightarrow Delta A_1B_1Csim Delta ABC$$

с коэффициентом подобия `ul (k = |cos C|`, `(/_A_1B_1C=/_B)`.

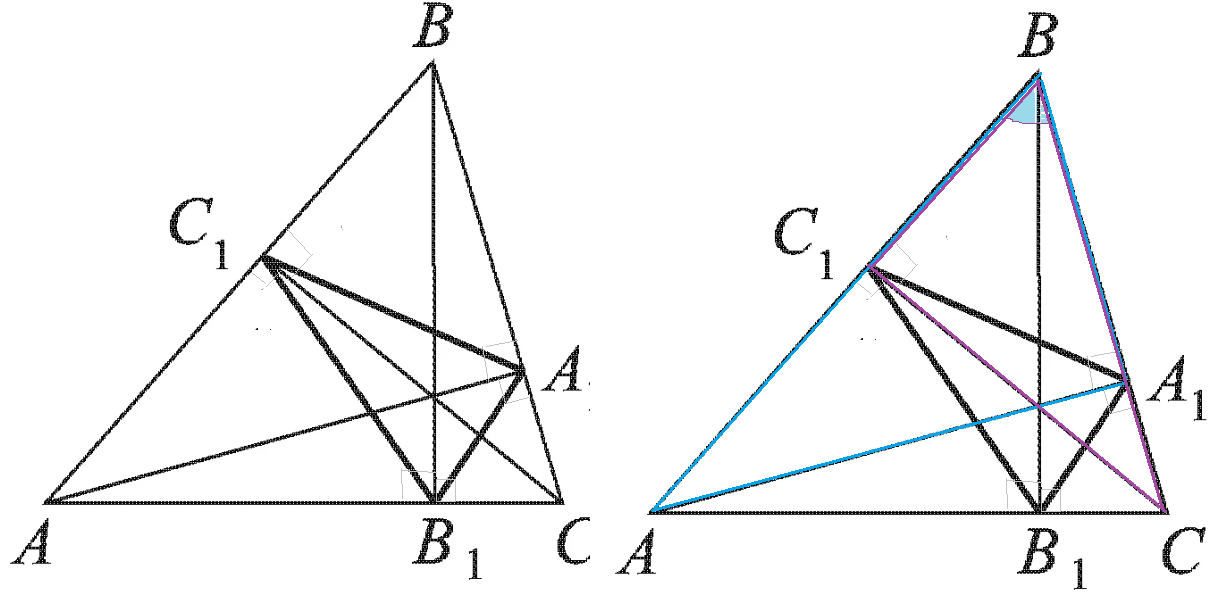
В остроугольном треугольнике `ABC` проведены высоты `A A_1`, `B B_1`, `C C_1` (рис. 13).

Треугольник, вершинами которого служат основания высот, называется «высотным» треугольником (или ортотреугольником).

Доказать, что лучи `A_1 A`, `B_1 B` и `C_1 C` являются биссектрисами углов высотного треугольника `A_1 B_1 C_1` (т. е. высоты остроугольного треугольника являются биссектрисами ортотреугольника).

По первой лемме о высотах `Delta A_1 B_1 C

Delta ABC`, `/_ A_1 B_1 C = /_ B`.

Аналогично `Delta AB_1C_1

Delta ABC`, `/_ AB_1 C_1 = /_ B`, т. е. `/_A_1 B_1C = /_ AB_1 C_1`.

Так как `BB_1` — высота, то `/_AB_1B = /_CB_1B = 90^@`.

Поэтому `/_C_1B_1B = /_A_1B_1B = 90^@ — /_B`, т. е. луч `B_1B` — биссектриса угла `A_1B_1C_1`.

Аналогично доказывается, что `A A_1` — биссектриса угла `B_1 A_1 C_1` и `C_1C` — биссектриса угла `B_1 C_1 A_1`.

Высоты `A A_1`, `B B_1` треугольника `ABC` пересекаются в точке `H` (рис. 14). Доказать, что имеет место равенство `AH * H A_1 = BH * HB_1`, т. е. произведение отрезков одной высоты равно произведению отрезков другой высоты.

Delta BHA_1`, имеют по равному острому углу при вершине `H` (заметим, что этот угол равен углу `C`). Из подобия следует `(AH)/(BH) = (HB_1)/(HA_1)`, откуда `AH * HA_1 = BH * HB_1`. Для тупоугольного треугольника утверждение также верно. Попробуйте доказать самостоятельно.

Высоты `A A_1` и `B B_1` треугольника `ABC` пересекаются в точке `H`, при этом `BH = HB_1` и `AH = 2 HA_1` (рис. 15). Найти величину угла `C`.

1. По условию пересекаются высоты, поэтому треугольник остроугольный. Положим `BH = HB_1 = x` и `HA_1 = y`, тогда `AH = 2y`. По второй лемме о высотах `AH * HA_1 = BH * HB_1`, т. е. `x^2 = 2y^2`, `x = y sqrt 2`.
2. В треугольнике `AHB_1` угол `AHB_1` равен углу `C` (т. к. угол `A_1 AC` равен `90^@ — C`), поэтому `cos C = cos (/_ AHB_1) = x/(2y) = sqrt 2/ 2`. Угол `C` — острый, `/_ C = 45^@`.

Установим ещё одно свойство биссектрисы угла треугольника.

Биссектриса внутреннего угла треугольника делит противолежащую этому углу сторону на отрезки, пропорциональные прилежащим сторонам, т. е. если `AD` — биссектриса треугольника `ABC`, то `(BD)/(DC) = (AB)/(AC)`.

Проведём через точку `B` прямую параллельно биссектрисе `DA`, пусть `K` — её точка пересечения с прямой `AC` (рис. 16).

Параллельные прямые `AD` и `KB` пересечены прямой `KC`, образуются равные углы `1` и `3`. Те же прямые пересечены и прямой `AB`, здесь равные накрест лежащие углы `2` и `4`. Но `AD` — биссектриса, `/_1 = /_2`, следовательно `/_3 = /_4`. Отсюда следует, что треугольник `KAB` равнобедренный, `KA = AB`.
По теореме о пересечении сторон угла параллельными прямыми из $$ ADVert KB$$ следует `(BD)/(DC) = (KA)/(AC)`. Подставляя сюда вместо `KA` равный ему отрезок `AB`, получим `(BD)/(DC) = (AB)/(AC)`. Теорема доказана.

Биссектриса треугольника делит одну из сторон треугольника на отрезки длиной `3` и `5`. Найти в каких пределах может изменяться периметр треугольника.

Пусть `AD` — биссектриса и `BD = 3`, `DC = 5` (рис. 17).

По свойству биссектрисы `AB : AC = 3:5`. Положим `AB = 3x`, тогда `AC = 5x`. Каждая сторона треугольника должна быть меньше суммы двух других сторон, т. е. `ul (5x 1`.

Периметр треугольника `P = 8 + 8x = 8(1 + x)`, поэтому `ul (16

Содержание

Подобные треугольники
Определение
Признаки подобия треугольников
Свойства подобных треугольников
Примеры наиболее часто встречающихся подобных треугольников
Задача 41353 Докажите пожалуйста Отрезок, соединяющий.
Условие
Решение
🎦 Видео

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Подобные треугольники

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Определение

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Видео:ПОДОБНЫЕ ТРЕУГОЛЬНИКИ коэффициент подобия 8 классСкачать

Признаки подобия треугольников

I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Видео:ПОДОБНЫЕ ТРЕУГОЛЬНИКИ 8 класс ЗАДАЧИ коэффициент подобияСкачать

Свойства подобных треугольников

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров подобных треугольников равно коэффициенту подобия.
Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

Видео:Средняя линия и коэффициент подобияСкачать

Примеры наиболее часто встречающихся подобных треугольников

1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Здесь вы найдете подборку задач по теме «Подобные треугольники» .

Видео:Коэффициент подобия отрезков/ площадей/ объемовСкачать

Задача 41353 Докажите пожалуйста Отрезок, соединяющий.

Условие

Докажите пожалуйста
Отрезок, соединяющий основания высот остроугольного треугольника, отсекает от данного
треугольника подобный ему с коэффициентом подобия, равным косинусу общего угла этих треугольников