Нормаль к плоскости заданной параллельными прямыми (7 видео)

Нормальный вектор плоскости, координаты нормального вектора плоскости

Существует ряд заданий, которым для решения необходимо нормальный вектор на плоскости, чем саму плоскость. Поэтому в этой статье получим ответ на вопрос определения нормального вектора с примерами и наглядными рисунками. Определим векторы трехмерного пространства и плоскости по уравнениям.

Содержание

Нормальный вектор плоскости – определение, примеры, иллюстрации
Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости
Векторы в пространстве и метод координат
Система координат в пространстве
Плоскость в пространстве задается уравнением:
Метод координат в пространстве: формулы и комментарии репетитора
Угол между прямыми а и b
Нормаль к плоскости
Угол между прямой и плоскостью
Угол между плоскостями
Уравнение плоскости в пространстве
Расстояние от точки до плоскости
Комментарий репетитора по математике :
💡 Видео

Видео:Построение следов плоскостиСкачать

Нормальный вектор плоскости – определение, примеры, иллюстрации

Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.

Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.

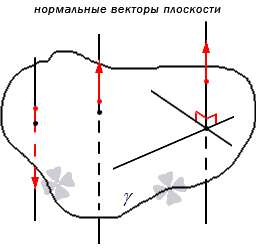
Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.

Нормальные векторы располагаются на параллельных прямых, поэтому они все коллинеарны. То есть, при нормальном векторе n → , расположенном в плоскости γ , вектор t · n → , имея ненулевое значение параметра t , также нормальный вектор плоскости γ . Любой вектор может быть рассмотрен как направляющий вектор прямой, которая перпендикулярна этой плоскости.

Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.

Рассмотрим на примере нормального вектора на плоскости.

Задана прямоугольная система координат О х у z в трехмерном пространстве. Координатные векторы i → , j → , k → считаются нормальными векторами плоскостей O y z , O x z и O x y . Это суждение верно, так как i → , j → , k → ненулевые и расположены на координатных прямых O x , O y и O z . Эти прямые перпендикулярны координатным плоскостям O y z , O x z и O x y .

Видео:Параллельность прямой к плоскостиСкачать

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости

Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат О х у z . Для определения нормального вектора n → = ( A , B , C ) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид A x + B y + C z + D = 0 . То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.

Найти координаты нормального вектора, принадлежащего плоскости 2 x — 3 y + 7 z — 11 = 0 .

По условию имеем уравнение плоскости. Необходимо обратить внимание на коэффициенты, так как они и являются координатами нормального вектора заданной плоскости. Отсюда получаем, что n → = ( 2 , — 3 , 7 ) — это нормальный вектор плоскости. Все векторы плоскости задаются при помощи формулы t · n → = 2 · t , — 3 · t , 7 · t , t является любым действительным числом не равным нулю.

Ответ: n → = ( 2 , — 3 , 7 ) .

Определить координаты направляющих векторов заданной плоскости x + 2 z — 7 = 0 .

По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение x + 2 z — 7 = 0 к виду 1 · x + 0 · y + 2 z — 7 = 0 . Отсюда получим, что координаты нормального вектора данной плоскости равны ( 1 , 0 , 2 ) . Тогда множество векторов будет иметь такую форму записи ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

Ответ: ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

При помощи уравнения плоскости в отрезках, имеющего вид x a + y b + z c = 1 , и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны 1 a , 1 b , 1 c .

Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.

Видео:Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Видео:19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Видео:Касательная плоскость и нормаль к поверхности в заданной точкеСкачать

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

То есть A + C + D = 0.

Аналогично для точки K:

Получили систему из трех уравнений:

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

Выразим C и B через A и подставим в третье уравнение:

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Метод координат в пространстве: формулы и комментарии репетитора

Метод координат — весьма эффективный и универсальный способ нахождения любых углов или расстояний между стереометрическими объектами в пространстве. Если Ваш репетитор по математике имеет высокую квалификацию, то он должен это знать. В противном случае я бы советовал для «С» части сменить репетитора. Моя подготовка к ЕГЭ по математике С1-С6 обычно включает разбор основных алгоритмов и формул, описанных ниже.

Угол между прямыми а и b

Углом между прямыми в пространстве называется угол между любыми параллельными им пересекающимися прямыми. Этот угол равен углу между направляющими векторами данных прямых (или дополняет его до 180 град).

Какой алгоритм использует репетитор по математике для поиска угла?

1) Выбираем любые вектора и , имеющие направления прямых а и b (параллельные им).
2) Определяем координаты векторов и по соответствующим координатам их начал и концов (от координат конца вектора нужно отнять координаты начала).
3) Подставляем найденный координаты в формулу:
. Для нахождения самого угла, нужно найти арккосинус полученного результата.

Нормаль к плоскости

Нормалью к плоскости называется любой вектор, перпендикулярный к этой плоскости.
Как найти нормаль? Для поиска координат нормали достаточно узнать координаты любых трех точек M, N и K, лежащих в данной плоскости. По этим координатам находим координаты векторов и и требуем выполнения условий и . Приравнивая скалярные произведение векторов к нулю, составляем систему уравнений с тремя переменными, из которой можно найти координаты нормали.

Замечание репетитора по математике : Совсем не обязательно решать систему полностью, ибо достаточно подобрать хотя бы одну нормаль. Для этого можно подставить вместо какой-нибудь из ее неизвестных координат любое число (например единицу) и решить систему двух уравнений с оставшимися двумя неизвестными. Если она решений не имеет, то это значит, что в семействе нормалей нет той, у которой по выбранной переменной стоит единица. Тогда подставьте единицу вместо другой переменной (другой координаты) и решите новую систему. Если опять промахнетесь, то Ваша нормаль будет иметь единицу по последней координате, а сама она окажется параллельной какой-нибудь координатной плоскости (в таком случае ее легко найти и без системы).

Угол между прямой и плоскостью

Допустим, что нам заданы прямая и плоскость координатами направляющего вектора и нормали
Угол между прямой и плоскость вычисляется по следующей формуле:

Угол между плоскостями

Пусть и — две любые нормали к данным плоскостям. Тогда косинус угла между плоскостями равен модулю косинуса угла между нормалями:

Уравнение плоскости в пространстве

Точки, удовлетворяющие равенству образуют плоскость с нормалью . Коэффициент отвечает за величину отклонения (параллельного сдвига) между двумя плоскостями с одной и той же заданной нормалью . Для того, чтобы написать уравнение плоскости нужно сначала найти ее нормаль (как это описано выше), а затем подставить координаты любой точки плоскости вместе с координатами найденной нормали в уравнение и найти коэффициент .

Расстояние от точки до плоскости

Для вычисления расстояния от точки до плоскости , заданной уравнением можно использовать следующую формулу:

В знаменателе стоит длина нормали, а числителе — значение выражения из левой части уравнения плоскости в точке

Комментарий репетитора по математике :

Методом координат можно находить не только углы и расстояния в пространстве, но и
1) площади многоугольников (треугольника, параллелограмма), расположенных в заданной плоскости.
2) объемы простейших многогранников (параллелепипедов и пирамид).

Для понимания таких формул нужно изучить понятия векторного и смешанного произведения векторов, а также определителя матрицы. В скором времени я сделаю для вычисления объемов соответствующую справочную страничку.

Средства аналитической геометрии репетитор по математике практически не использует в работе со средним и тем более слабым учеником. И очень жаль, что загруженность среднестатистического сильного школьника не позволяет репетитору провести более-менее серьезную работу на уровне определений из высшей математики и с соответствующей практикой решения задач. Поэтому я часто ограничиваюсь простым сообщением формул и демонстрацией одного – двух примеров их использования. В школьной программе не предусмотрено время для изучения векторных приемов вообще, однако на ЕГЭ Вы имеете право решать задачу С2 любым из известных науке способов. Отсюда мораль: учите координаты. Расширенная подготовка к ЕГЭ по математике с изучением приемов аналитической геометрии даст Вам мощное и универсальное средство для решения огромного класса задач типа С2. Пользуйтесь этой страничкой на здоровье!

Колпаков А.Н. Репетитор по математике Москва (Строгино).

Спасибо Вам за этот материал,все наглядно и понятно.