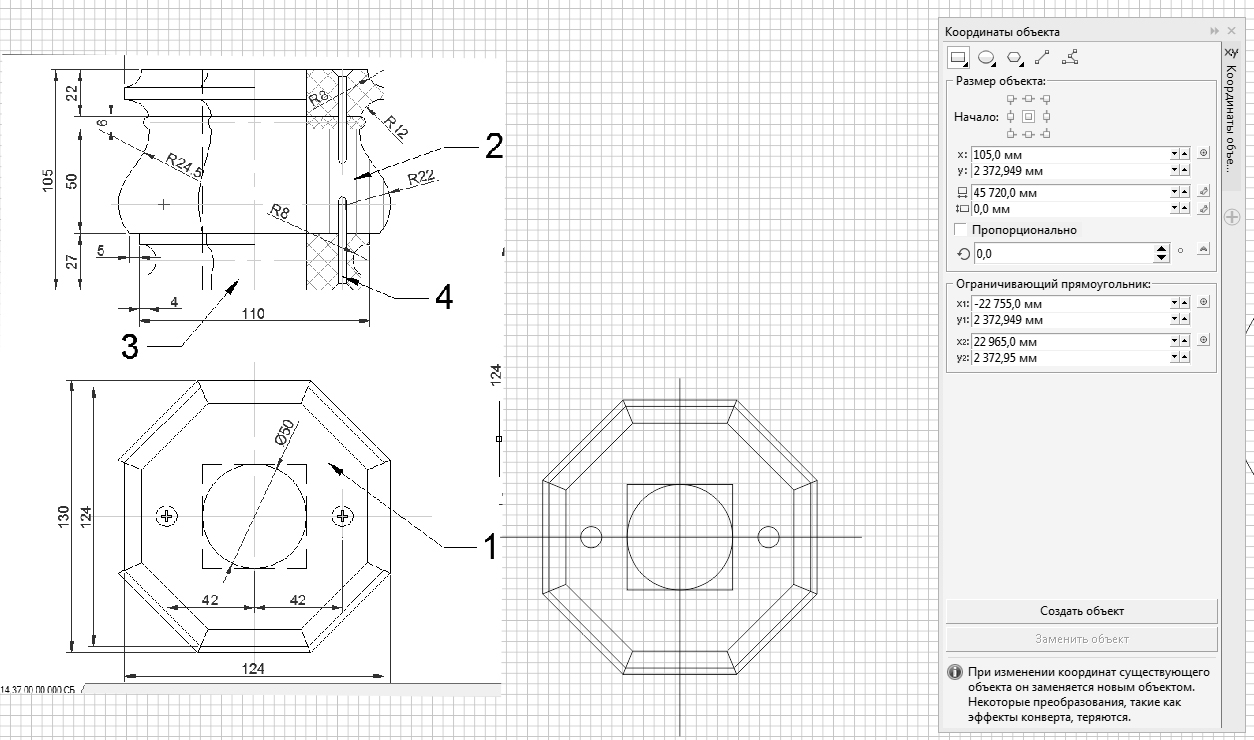
Доброго времени суток, уважаемые посетители сайта. Тема урока — инструмент «Координаты объекта» в CorelDRAW. Данный инструмент используется для точного черчения и точного изменения уже готовых объектов. При помощи данного инструмента возможно точное построение прямоугольников, кругов, эллипсов, многоугольников. И самое главное, вы сможете точно и быстро строить линии нужной вам длины и с нужным углом наклона (длина линий и углы вводятся с клавиатуры) и от нужной базы, которую возможно указать вручную. Помимо вышеперечисленного, данный инструмент поможет вам точно перемещать вершины уже построенных объектов (инструмент многоточечная линия). Также при помощи данного инструмента вы без труда сможете быстро разделить окружность на равные части. Обобщая вышесказанное, можно смело утверждать, что данный инструмент крайне необходим для точного построения в CorelDRAW чертежей и векторов для фрезерных станков с ЧПУ (числовым программным управлением).
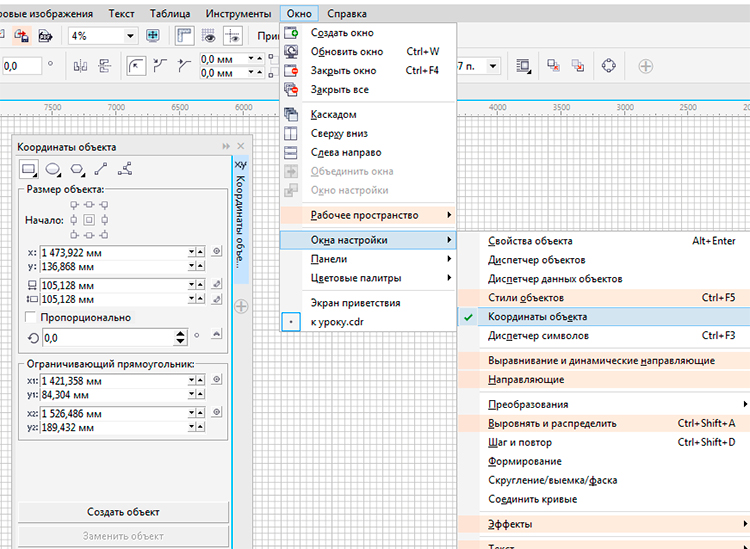
Получить доступ к инструменту «Координаты объекта» можно выбрав сверху в текстовом меню «Окно»-«Окна настройки»- «Координаты объекта». См. Рис.1
Рис.1
Запустив данное окно мы получаем доступ к пяти разным инструментам точного черчения :
- Рисование прямоугольников и квадратов
- Рисование эллипсов и кругов
- Рисование многоугольников
- Рисование двухточечной линии
- Рисование многоточечной линии
Рассмотрим все инструменты подробнее.
Рисование прямоугольников и квадратов. Окно данного инструмента визуально разбито на две области: размер объекта и ограничивающий прямоугольник.
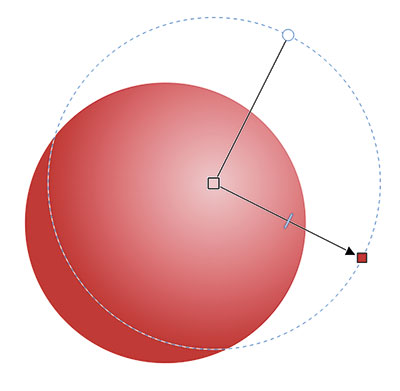
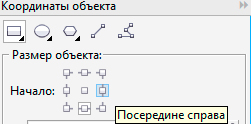
В размере объекта мы можем указывать базу, от которой будут считаться изменения выбранного объекта либо построение нового, также базовая точка учитывается при вращении объекта См. Рис.2
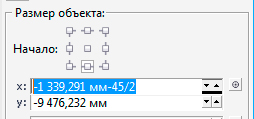
Далее содержатся числовые поля, в которые, вводя числовые данные, мы можем перемещать объект по X и У (данные числовые поля поддерживают простые арифметические операторы («+» «-» «*» «/» «()» и др.) См. Рис.3
Далее содержатся числовые поля, задающие размеры, через которые можно задавать размеры прямоугольника .
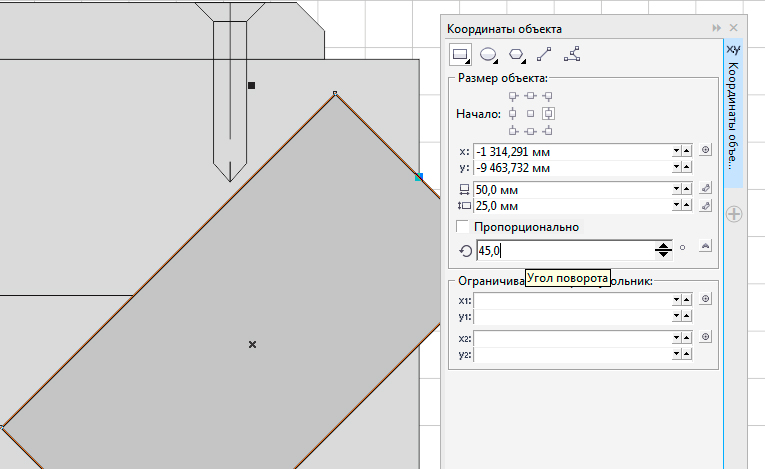
Далее содержится числовое поле угла поворота объекта (вращение объекта будет осуществляется согласно базовой точки, выставленной ранее) См. Рис.4
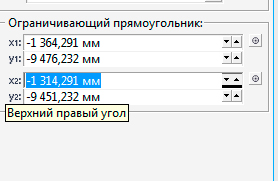
Вторая часть окна «Рисование прямоугольников и квадратов» содержит числовые поля инструмента «Ограничивающий прямоугольник». Здесь мы можем менять размеры ограничивающего объекта, в который вписан наш объект. См. Рис.5
Также обращаю ваше внимание, что справа напротив большинства числовых полей содержится кнопка интерактивного задания точки (при помощи мышки).
Более наглядную работу с инструментом «Рисование прямоугольников и квадратов» см. в видео 1
Видео 1
Рисование эллипсов и кругов и рисование многоугольников имеют интуитивно понятные параметры. Данными инструментами мы воспользуемся чуть позже в ходе выполнения практической работы «Черчение части колонны капители вида сверху». Единственное, на что бы хотелось сделать акцент — это то, что при помощи данных инструментов без труда можно разделить окружность на нужное количество равных частей. См.Видео 2
Видео 2
Инструмент «Рисование двухточечной линии». Данный инструмент поможет нам в построении точных линий либо точном изменении уже построенных ранее линий чертежей и векторов для фрезерных станков с ЧПУ. Также он позволит нам задавать точные углы поворота линий. Также данный инструмент можно применять как измерительный. Чтобы более полно понять принцип работы построения точной линии выполним следующую практическую работу. Расчертим ножку табуретки по заранее известным размерам. См. Видео 3.
Видео 3
Как мы наблюдаем из видео, инструмент «Рисование двухточечной линии» очень хорошее дополнение классической ломаной линии, когда дело доходит до точного параметрического черчения.
Далее на рассмотрении у нас остался инструмент «Многоточечная линия». При помощи данного инструмента удобно изменять координаты точек объекта, построенного сложной многоузловой линией. При выделении объекта и переходе к «Многоточечная линия», мы увидим все координаты узлов выделенного объекта. Далее данные координаты мы можем изменять, тем самым изменяя точно форму векторного объекта. Рассмотрим данный инструмент на конкретном примере. У нас имеется вектор филенки высотой 500 мм. Нам необходимо уменьшить высоту филенки до 400 мм, не искажая пропорции филенки. См. Видео 4
Видео 4
В завершение изучения прикрепленного окна «Координаты объекта», выполним более сложное построение «Черчение части колонны капители вида сверху». Вектор чертежа в дальнейшем будет использоваться для создания управляющей программы для фрезерного станка с ЧПУ См. Рис.6
Рис.6
Последовательность построения будет следующей.
Выберем в окне «Координаты объекта» инструмент «Рисование многоугольников».
Зададим диаметр многоугольника 140,71 мм.
Зададим количество углов — 8.
Укажем поворот многоугольника на 202,5 градуса.
Построим окружность, используя инструмент «Рисование эллипсов и кругов».
Зададим диаметр окружности — 50 мм.
Построим автоматически квадрат, описывающий окружность. Для этого воспользуемся инструментом «Рисование прямоугольников и квадратов».
Построим головки саморезов, используя инструмент «Рисование эллипсов и кругов», и через ввод в соответствующие числовое поле «+ 42 мм», сместим автоматически получившиеся окружности на нужное удаление от центра.
Далее используя инструмент «Контур» и «Свободная форма», дочертим часть капители колонны вида сверху. См. Видео 5
Видео 5
Подведем итог. Инструмент «Координаты объекта» в CorelDRAW незаменим в точном параметрическом черчении векторов для фрезерных станков с ЧПУ и позволяет решать достаточно быстро определенные графические задачи.
Также, прежде чем использовать CorelDRAW в точном черчении, я рекомендую ознакомиться со следующими статьями:
Также рекомендую вам ознакомиться со следующим статьями:
- Шестиугольник описанный около окружности построение
- Определение и построение
- Свойства простые и интересные
- Описанная окружность и возможность построения
- Вписанная окружность
- Периметр и площадь
- Занимательные построения
- От теории к практике
- Похожие презентации
- Презентация на тему: » а) Для построения правильного шестиугольника можно воспользоваться тем, что а 6 = R. Построение. 1. Строим ω(О; R). О 2. Строим произвольную точку, принадлежащую.» — Транскрипт:
- Компью А рт
- Нанизываем ожерелье
- Вешаем гирлянду
- Меняем порядок расположения объектов
- Заключение
- 📺 Видео
Видео:Размещение надписи по кругу в CorelDrawСкачать

Шестиугольник описанный около окружности построение

Видео:Как быстро распределить объекты по окружности в Corel DrawСкачать

Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
чертится прямая линия и на ней ставится точка;
- из этой точки строится окружность (она является ее центром);
- из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
- после этого отрезками последовательно соединяются все точки на первой окружности.
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Видео:Как построить правильный шестиугольник.Скачать

Свойства простые и интересные
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.
Описанная окружность и возможность построения
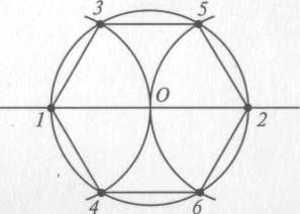
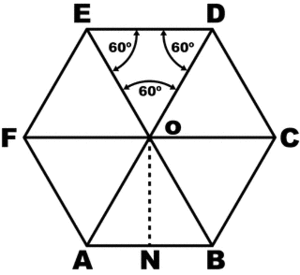
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
R=а.
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
Ну а площадь этой окружности будет стандартная:
S=πR²
Вписанная окружность
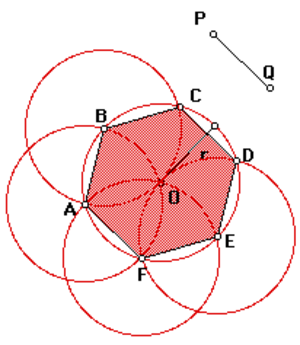
Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2.
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а, или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
Занимательные построения
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
- Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
- Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
- Углы новообразованного шестиугольника равняются 360-120-60-60=120°.
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
Площадь нового шестиугольника можно посчитать так:
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
Видео:Геометрия - Построение шестиугольникаСкачать

От теории к практике
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
Презентация была опубликована 5 лет назад пользователемГригорий Оськин
Похожие презентации
Видео:Как нарисовать многоугольник в Corel DrawСкачать

Презентация на тему: » а) Для построения правильного шестиугольника можно воспользоваться тем, что а 6 = R. Построение. 1. Строим ω(О; R). О 2. Строим произвольную точку, принадлежащую.» — Транскрипт:
2 а) Для построения правильного шестиугольника можно воспользоваться тем, что а 6 = R. Построение. 1. Строим ω(О; R). О 2. Строим произвольную точку, принадлежащую окружности. 3. Из данной точки раствором циркуля равным R на окружности откладываем последовательно один за другим отрезки. (таким образом окружность разделиться на 6 равных частей). 4. Соединив последовательно данные точки, получим правильный шестиугольник. б) Для построения правильного шестиугольника можно воспользоваться другим способом (см. учебник стр.206, п. 117).
3 Построение. 1. Строим ω(О; R). О 2. Строим произвольную точку, принадлежащую окружности. 3. Из данной точки раствором циркуля равным R на окружности откладываем последовательно один за другим отрезки. (таким образом окружность разделиться на 6 равных частей). 4. Соединив последовательно через одну данные точки, получим правильный треугольник. Для построения правильного треугольника воспользуемся тем же алгоритмом, что и для построения правильного шестиугольника, только получив 6 точек на окружности, соединим их через одну.
4 Построение. 1. Строим ω(О; R). О 4. Соединив последовательно точки пересечения прямых с окружностью, получим правильный треугольник. Для построения правильного четырехугольника следует провести две перпендикулярные прямые, проходящие через центр окружности. Соединив последовательно точки пересечения прямых с окружностью, получим правильный четырехугольник (квадрат). 2. Проведем произвольную прямую, проходящую через центр окружности. 3. Проведем прямую, перпендикулярную данной и проходящую через центр окружности.
5 Построение. О 3. Соединив последовательно точки на окружности получим правильный восьмиугольник. Для построения правильного восьмиугольника сначала строим правильный четырехугольник ( по описанному алгоритму), а затем проводим две прямые через середины противолежащих сторон. При этом окружность окажется разделенной на 8 раваных частей. Соединив последовательно точки на окружности, получим правильный восьмиугольник. 1. Строим правильный четырехугольник, вписанный в окружность. 2. Проводим две прямые через середины сторон квадрата (вершины квадрата и точки пересечения прямых с окружностью делят окружность на 8 равных частей).
6 Рассмотренные способы построения правильных многоугольников дают возможность построить многоугольники, вписанные в окружность. Чтобы построить многоугольник, описанный около окружности, пользуются теми же способами, только на последнем этапе не соединяют полученные точки на окружности, а проводят через них касательные. Построим правильный шестиугольник, описанный около окружности. Построение. 1. Строим ω(О; R). О 2. Строим произвольную точку, принадлежащую окружности. 3. Из данной точки раствором циркуля равным R на окружности откладываем последовательно один за другим отрезки. 4. Через каждую полученную точку на окружности проводим касательные. Получим правильный шестиугольник.
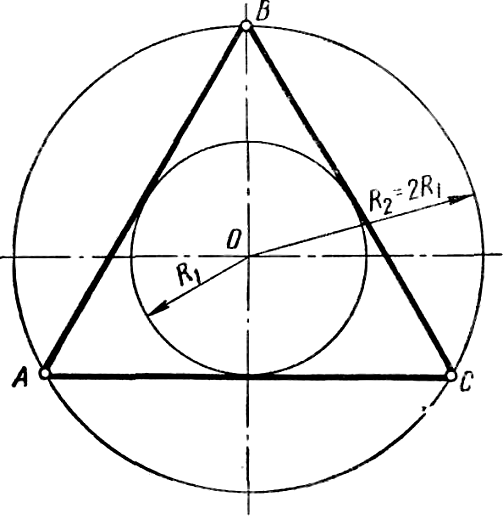
Правильный описанный треугольник строят следующим образом (рисунок 38). Из центра заданной окружности радиуса R1 проводят окружность радиусом R2 = 2R1 и делят ее на три равные части. Точки деления А, В, С являются вершинами правильного треугольника, описанного около окружности радиуса R1.
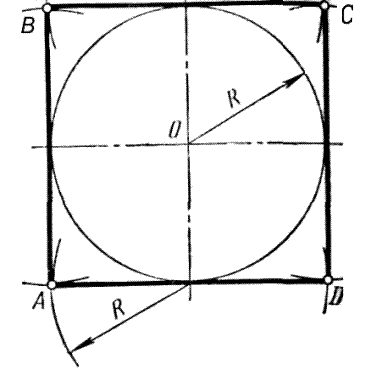
Правильный описанный четырехугольник (квадрат) можно построить с помощью циркуля и линейки (рисунок 39). В заданной окружности проводят два взаимно перпендикулярных диаметра. Приняв точки пересечения диаметров с окружностью за центры, радиусом окружности R описывают дуги до взаимного их пересечения в точках А, В, С,D. Точки A, B, C, D и являются вершинами квадрата, описанного около данной окружности.
Для построения правильного описанного шестиугольника необходимо вначале построить вершины описанного квадрата указанным выше способом (рисунок 40, а). Одновременно с определением вершин квадрата заданную окружность радиуса R делят на шесть равных частей в точках 1, 2, 3, 4, 5, 6 и проводят вертикальные стороны квадрата. Проведя через точки деления окружности 2–5 и 3–6 прямые до пересечения их с вертикальными сторонами квадрата (рисунок 40, б), получают вершины А, В, D, Е описанного правильного шестиугольника.
Остальные вершины C и F определяют с помощью дуги окружности радиуса OA, которая проводится до пересечения ее с продолжением вертикального диаметра заданной окружности.
3 СОПРЯЖЕНИЯ
Дата добавления: 2014-11-06 ; Просмотров: 4403 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Видео:Как из квадратного сделать круглое или подрезаем картинку по форме объекта.Corel Draw от ДеревяшкинаСкачать
Компью А рт
Хорошим подспорьем для пользователей, работающих с графическими редакторами, являются функции, позволяющие автоматизировать выполнение рутинных операций и за счет этого ускорить реализацию художественного замысла. На этом занятии мы рассмотрим возможности и особенности одной из весьма полезных функций графического редактора CorelDRAW, которая позволяет расположить выделенные объекты по выбранному пути произвольной формы.
В процессе работы над изображениями периодически возникает необходимость расположить несколько разных объектов (или копий одного исходного объекта) по определенной траектории, отличной от прямой линии. Простейшие примеры — это создание рисунка ожерелья, гирлянды и т.д.
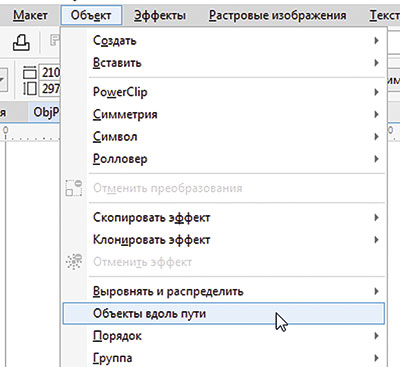
Для выполнения подобных операций в графическом редакторе CorelDRAW предусмотрена специальная функция — Объекты вдоль пути. Она позволяет автоматически расположить выделенные объекты вдоль выбранного пути, в качестве которого можно использовать любую кривую или фигуру.
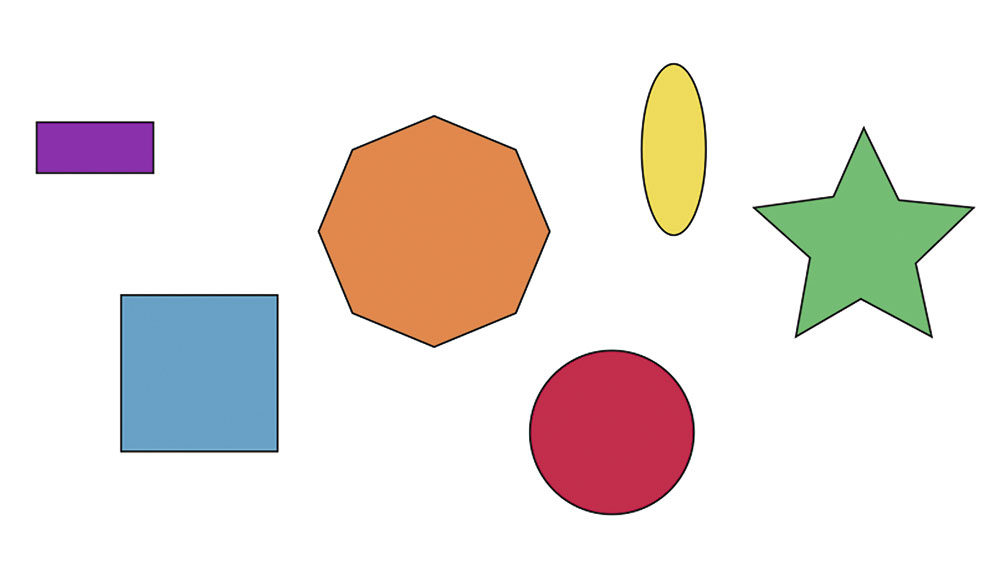
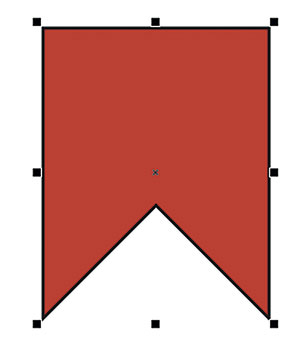
Знакомство с этой функцией начнем с рассмотрения простого примера. Создайте несколько объектов разной формы (рис. 1). При помощи инструмента Эллипс (F7) создайте окружность, как показано на рис. 2. Она послужит траекторией, вдоль которой будут размещены остальные объекты.
Рис. 1. Набор исходных объектов
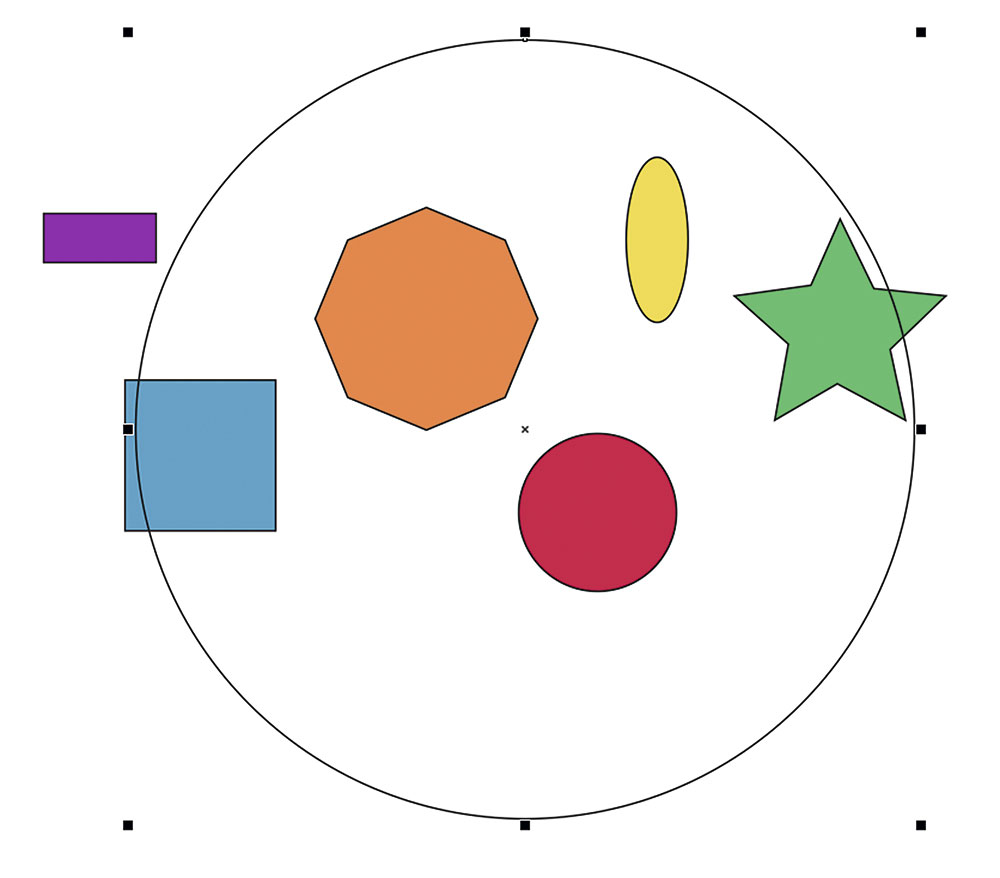
Рис. 2. Создана окружность, которая будет использоваться в качестве траектории
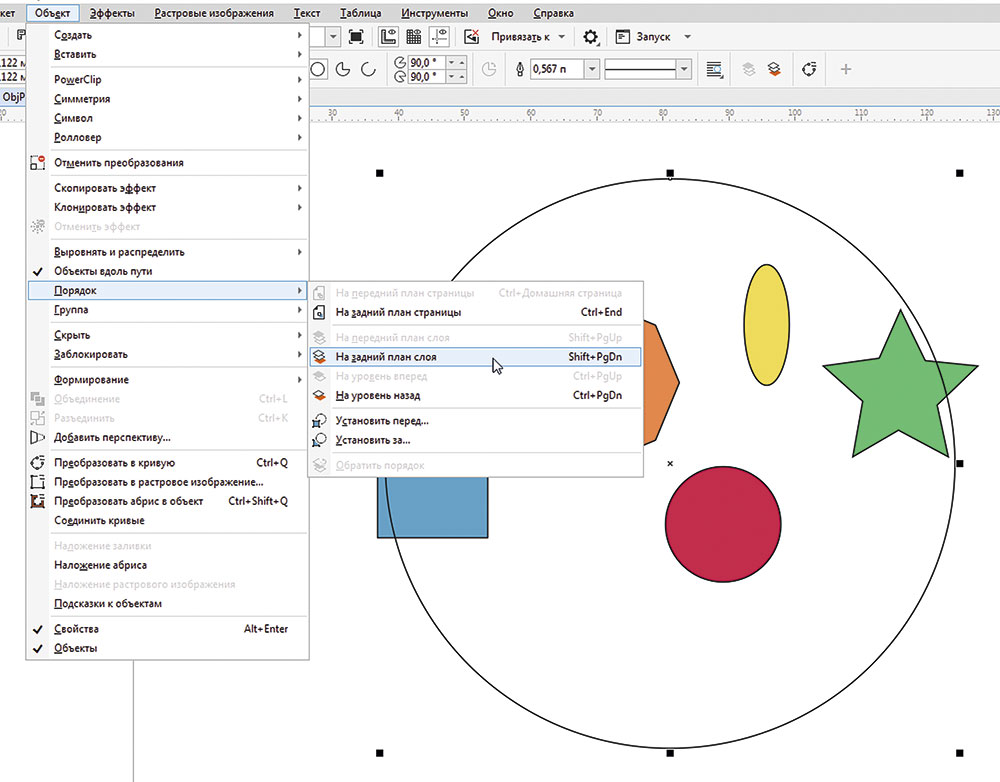
Необходимо учитывать, что при выделении сразу всех объектов по умолчанию в качестве траектории используется тот, который расположен ниже остальных. Чтобы переместить ранее созданную окружность на нижний план, выберите в меню Объект -> Порядок -> На задний план слоя (рис. 3) либо нажмите сочетание клавиш ShiftPgDn.
Рис. 3. Перемещение окружности на задний план слоя
Рис. 4. Включение отображения палитры Объекты вдоль пути в главном меню
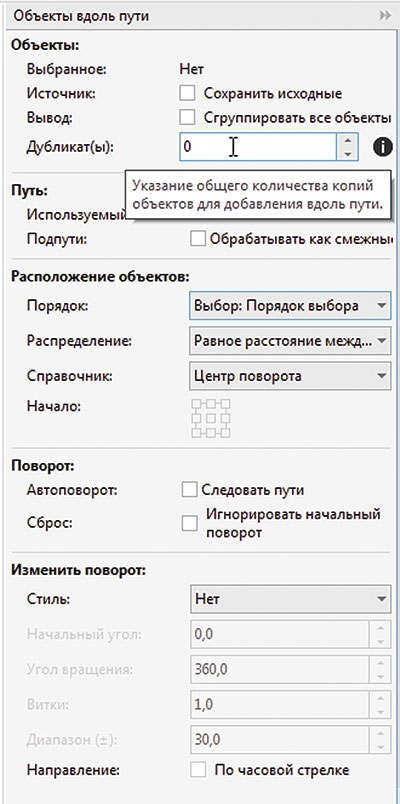
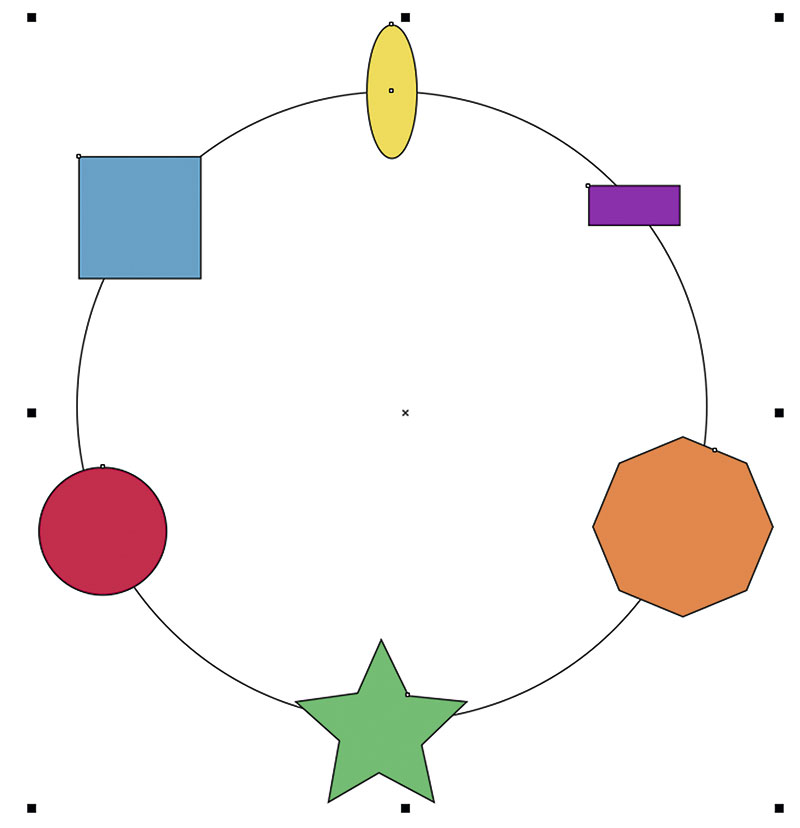
Переключитесь на инструмент выбора и выделите все объекты. Чтобы отобразить палитру настроек функции Объекты вдоль пути, выберите в главном меню Объект -> Объекты вдоль пути (рис. 4). Убедитесь, что в поле Дубликат(ы) введено значение «0», а все опции отключены (рис. 5). Нажмите кнопку Применить в нижней части палитры. Теперь объекты расположены по окружности с равными интервалами (рис. 6).
Рис. 5. Палитра настроек функции Объекты вдоль пути
Рис. 6. Исходные объекты расположены по окружности
Видео:Текст вдоль пути, оболочка или постигаем Corel Draw вместе с ДеревяшкинымСкачать

Нанизываем ожерелье
Функция Объекты вдоль пути позволяет располагать по выбранной траектории не только группу выделенных объектов, но и заданное количество копий одного исходного объекта. Чтобы понять, как это сделать, создадим стилизованное изображение ожерелья, составленного из одинаковых «бусин».
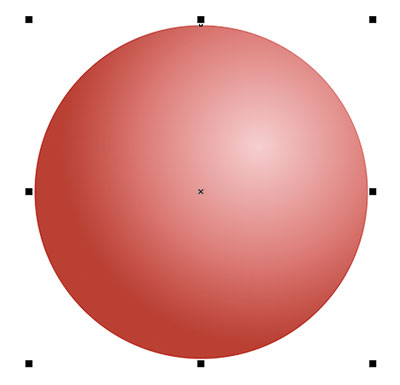
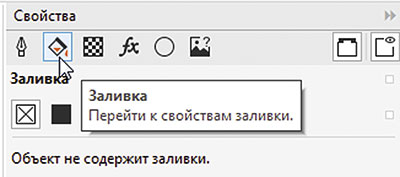
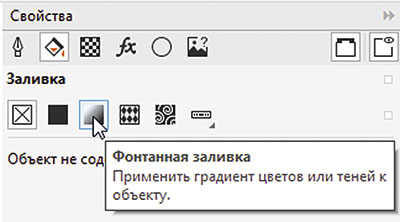
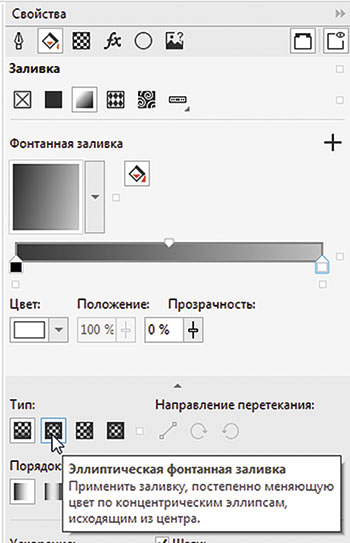
Начнем с исходного объекта. При помощи инструмента Эллипс создайте окружность и выберите для нее режим без абриса и радиальную градиентную заливку, как показано на рис. 7. Для этого включите отображение палитры Свойства1, выбрав в меню Окно -> Окна настройки -> Свойства или нажав сочетание клавиш AltEnter. Выберите раздел Заливка (рис. 8), а затем подраздел Фонтанная заливка (рис. 9), последовательно щелкнув по одноименным пиктограммам в верхней части палитры. После этого нажмите на пиктограмму Эллиптическая фонтанная заливка (рис. 10).
Рис. 7. Исходный объект
Рис. 8. Выбор раздела Заливка в палитре Свойства
Рис. 9. Выбор подраздела Фонтанная заливка в палитре Свойства
Рис. 10. Выбор режима нужного типа фонтанной заливки в палитре Свойства
Задайте для начальной узловой точки цвет R=227 G=30 B=36, а для конечной — R=243 G=197 B=199 (прозрачность 0%). Чтобы сместить центр заливки относительно центра окружности, воспользуйтесь инструментом Интерактивная заливка (рис. 11), который активируется нажатием клавиши G.
Рис. 11. Настройка фонтанной заливки при помощи инструмента Интерактивная заливка
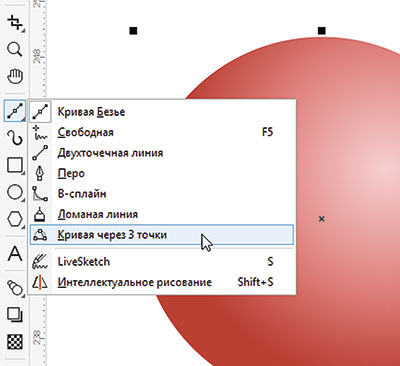
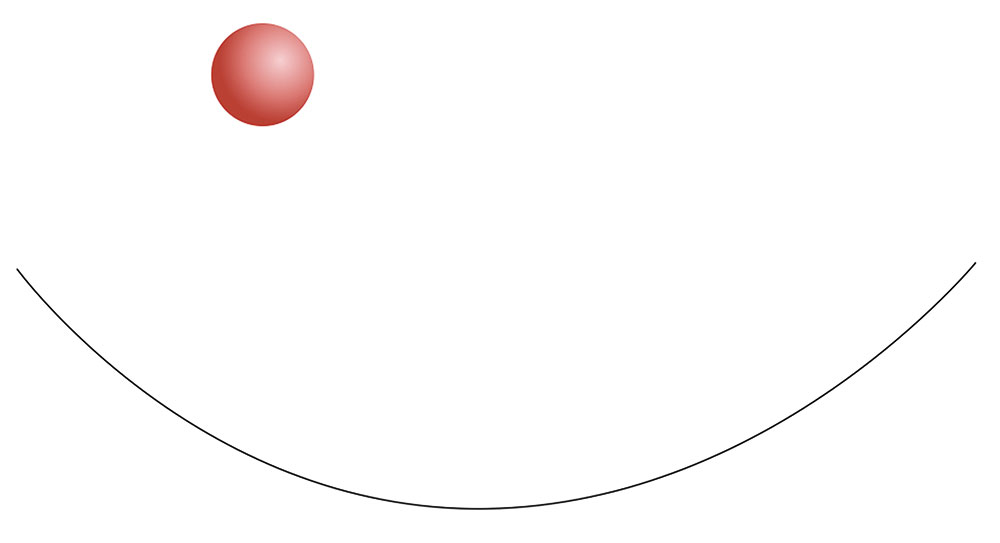
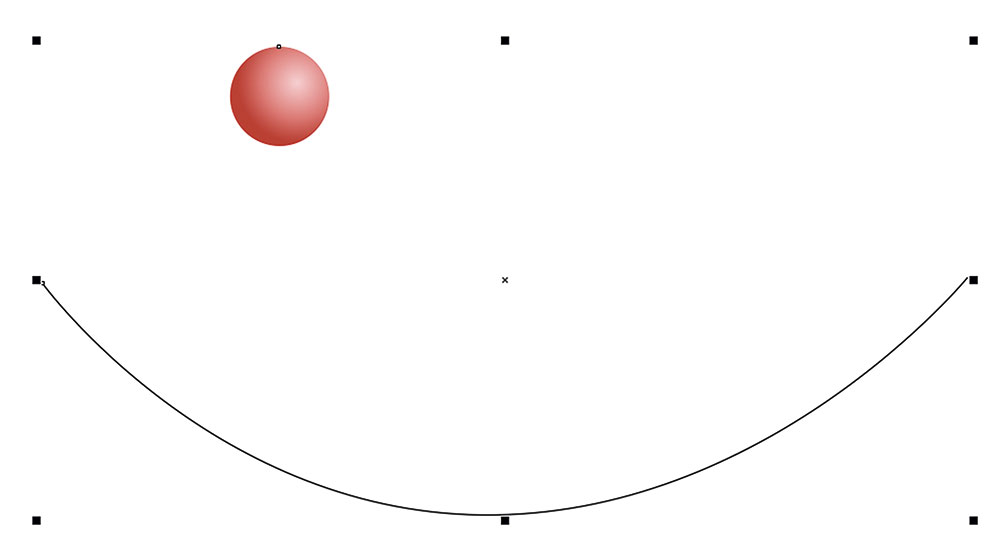
Переключитесь на инструмент Кривая через 3 точки (рис. 12) и создайте дугу, как показано на рис. 13. Не снимая выделения, переместите этот объект на нижний план слоя, нажав сочетание клавиш ShiftPgDn.
Рис. 12. Пиктограмма включения инструмента Кривая через 3 точки на панели инструментов
Рис. 13. Создание дуги
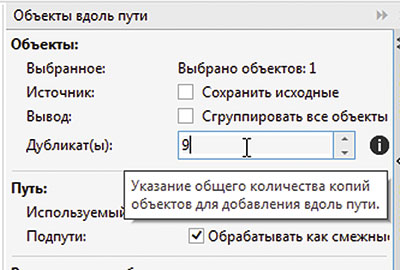
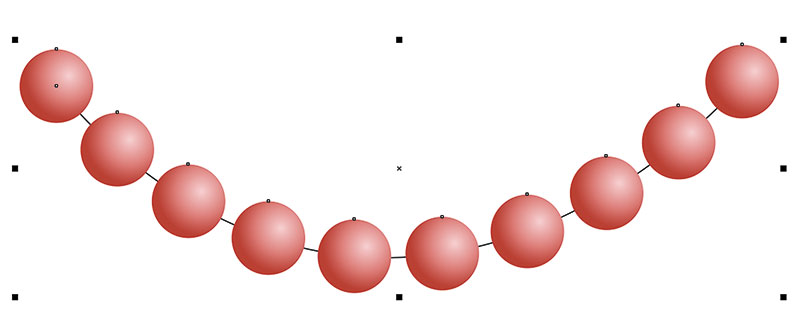
Снимите выделение. Переключитесь на инструмент выбора и выделите оба объекта (рис. 14). В палитре настроек Объекты вдоль пути введите в поле Дубликат(ы) значение «9» (рис. 15) и нажмите кнопку Применить. Результатом выполнения этих действий стало изображение, напоминающее бусины, нанизанные на нитку (рис. 16).
Рис. 14. Выделение объектов
Рис. 15. Ввод количества копий исходного объекта в палитре настроек Объекты вдоль пути
Рис. 16. Копии исходного объекта расположены по дуге
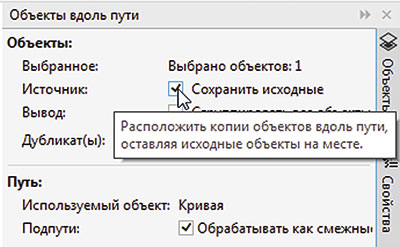
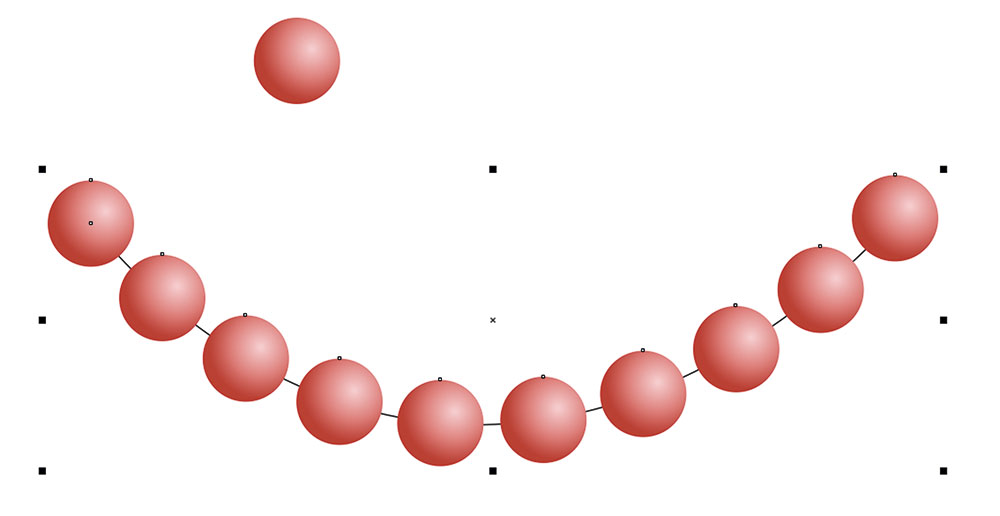
Если в палитре настроек Объекты вдоль пути включить опцию Сохранить исходные (рис. 17), то исходный объект после нажатия кнопки Применить останется на прежнем месте (рис. 18).
Рис. 17. Включение опции Сохранить исходные в палитре настроек Объекты вдоль пути
Рис. 18. Исходный объект сохранен после создания группы копий, расположенных по дуге
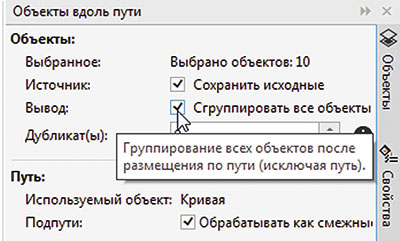
При активации опции Сгруппировать все объекты (рис. 19) все объекты, расположенные вдоль пути, будут автоматически объединены в одну группу (за исключением того, который используется в качестве траектории).
Рис. 19. Включение опции Сгруппировать все объекты в палитре настроек Объекты вдоль пути
Видео:Уроки CorelDRAW: шестиугольники - создаем орнаментыСкачать

Вешаем гирлянду
В некоторых случаях при размещении объектов вдоль траектории необходимо поворачивать их определенным образом. Такая возможность предусмотрена в настройках функции Объекты вдоль пути.
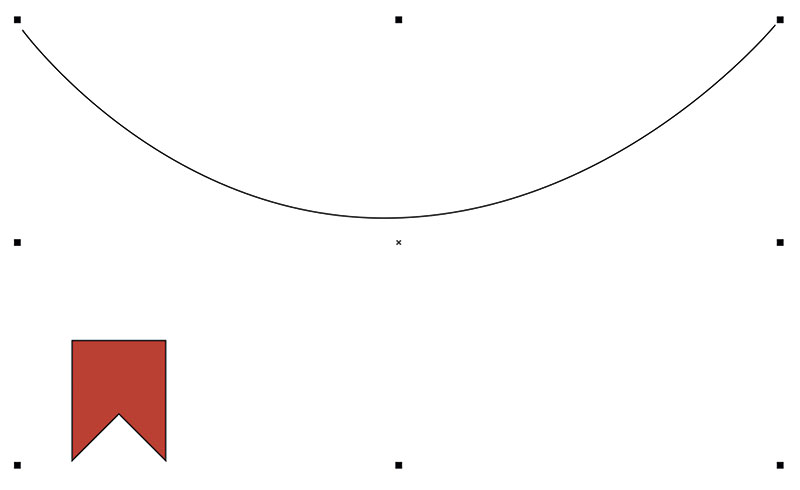
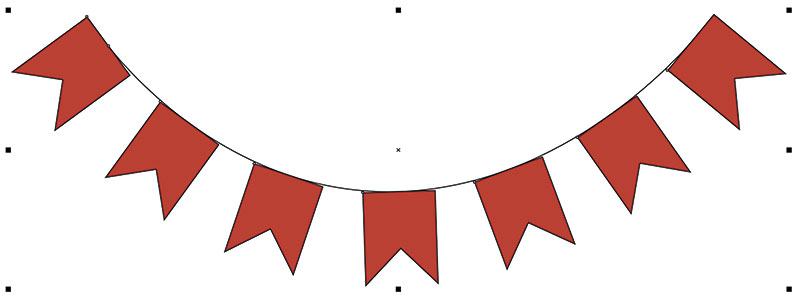
В качестве примера рассмотрим процесс создания схематического изображения гирлянды с флажками. Выделите дугу, использовавшуюся в качестве траектории в предыдущем примере, и скопируйте ее на новую страницу.
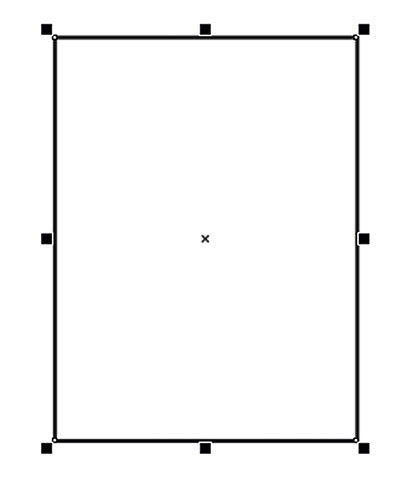
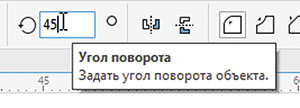
При помощи инструмента Прямоугольник (F6) создайте прямоугольник с соотношением сторон примерно 2:3 (рис. 20), а затем квадрат (рис. 21). Не снимая выделения, поверните квадрат на 45°, введя соответствующее значение в поле угла поворота объекта на панели свойств (рис. 22).
Рис. 20. Создание прямоугольника
Рис. 21. Создание квадрата
Рис. 22. Поле ввода числового значения угла поворота объекта на панели свойств
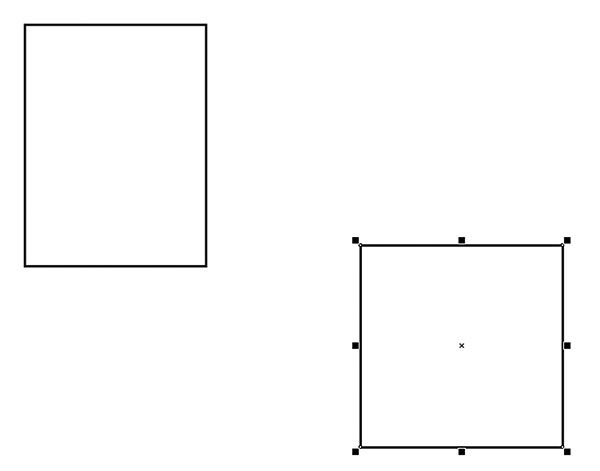
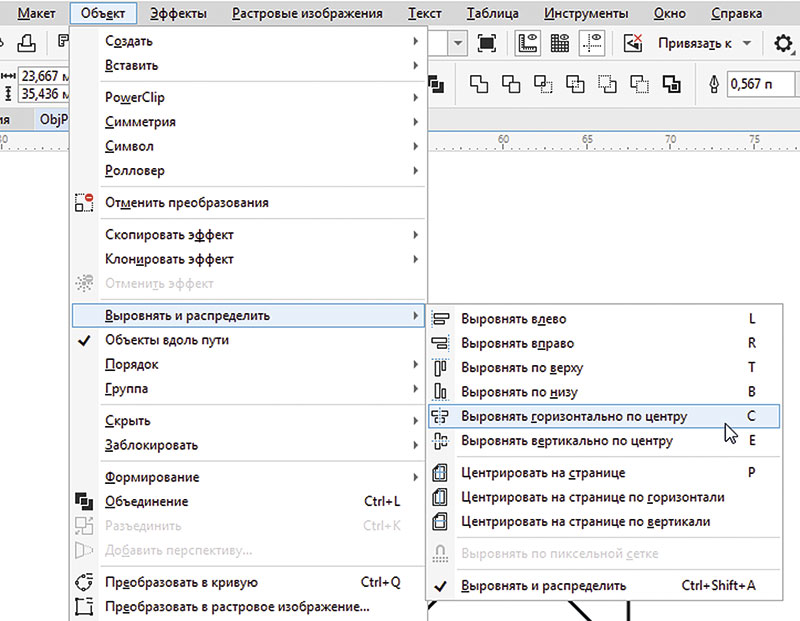
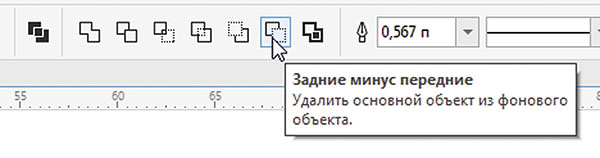
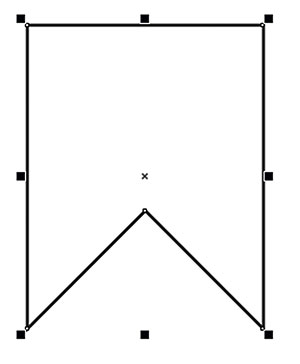
Переключитесь на инструмент выбора и переместите квадрат, как показано на рис. 23. Добавьте к выделению прямоугольник и выровняйте объекты по центру относительно горизонтали, выбрав в меню Объект -> Выровнять и распределить -> Выровнять горизонтально по центру (рис. 24) или нажав клавишу с буквой С. Щелкните по пиктограмме Задние минус передние на панели свойств (рис. 25). Контур «флажка» готов (рис. 26). Задайте для этого объекта однородную заливку какимлибо цветом (рис. 27).
Рис. 23. Перемещение квадрата
Рис. 24. Выбор функции выравнивания выделенных объектов по центру относительно горизонтали в главном меню
Рис. 25. Пиктограмма Задние минус передние на панели свойств
Рис. 26. Контур «флажка» готов
Рис. 27. Заливка объекта
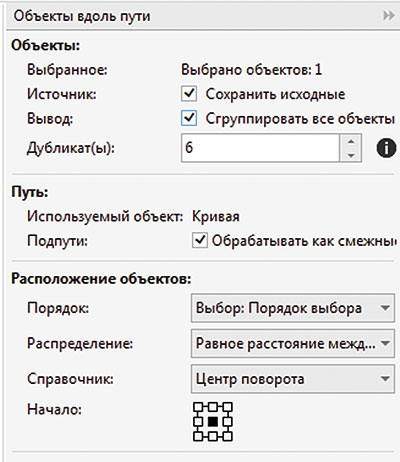
Добавьте к выделению кривую в виде дуги (рис. 28). В палитре настроек Объекты вдоль пути включите опции Сохранить исходные и Сгруппировать все объекты, а в поле Дубликат(ы) введите значение «6» (рис. 29). Нажмите кнопку Применить. На полученном изображении копии исходного объекта размещены вдоль выбранной траектории, однако все они расположены строго вертикально (рис. 30). Чтобы получить изображение гирлянды, необходимо каждый из размещаемых объектов повернуть на угол, равный углу наклона касательной в данной точке траектории. Давайте разберемся, как это сделать.
Рис. 28. Добавление дуги к выделению
Рис. 29. Настройки палитры Объекты вдоль пути
Рис. 30. Полученный результат не соответствует замыслу
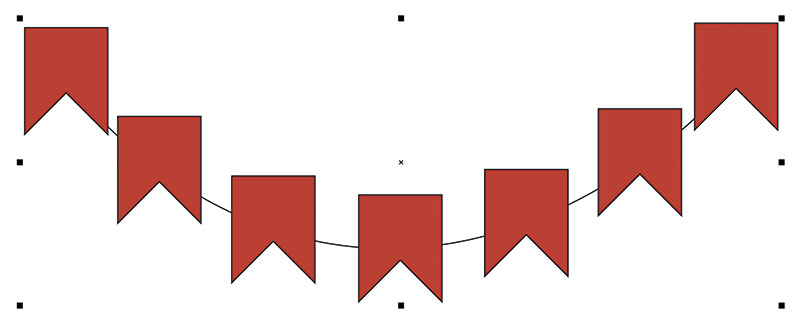
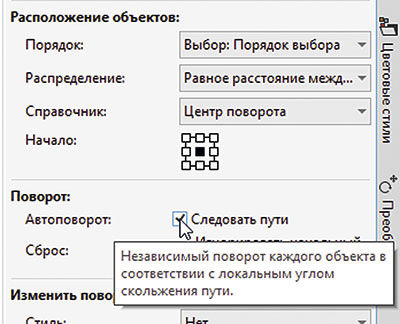
Выделите группу флажков, расположенных по траектории, и удалите ее. Затем выделите исходный объект и дугу. В палитре настроек Объекты вдоль пути включите опцию Следовать пути (рис. 31). Чтобы «флажки» крепились к гирлянде по верхнему краю, выберите положение начальной точки по центру сверху (рис. 32). Нажмите кнопку Применить. Теперь изображение гирлянды выглядит так, как и было задумано (рис. 33).
Рис. 31. Активация опции Следовать пути в палитре настроек Объекты вдоль пути
Рис. 32. Выбор положения начальной точки исходного объекта в палитре настроек Объекты вдоль пути
Рис. 33. Теперь гирлянда выглядит так, как было задумано
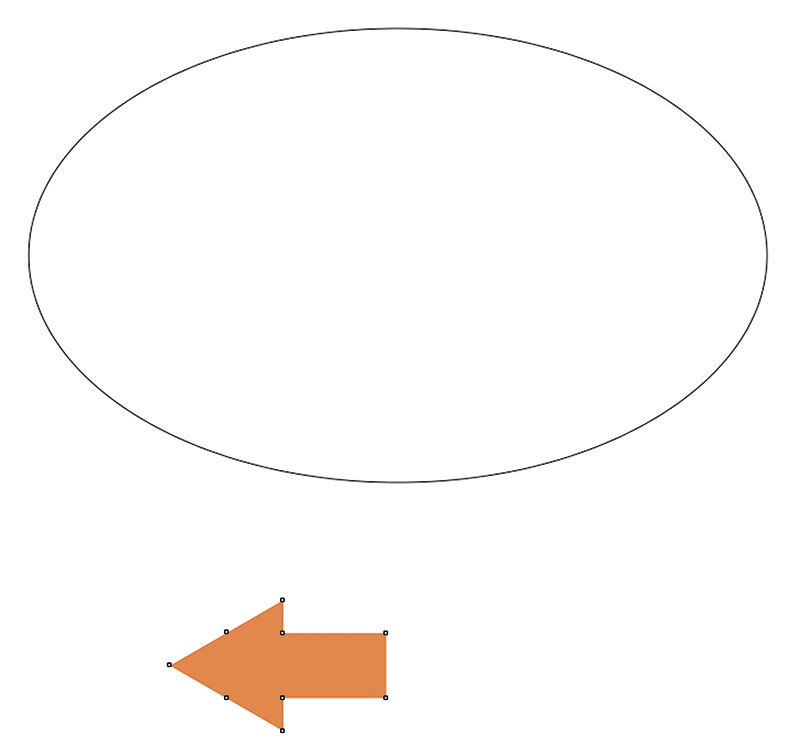
В некоторых случаях возникает необходимость располагать копии исходного объекта под определенным углом к траектории. Например, требуется расположить несколько копий стрелки (рис. 34) по эллиптической траектории (рис. 35) таким образом, чтобы все они указывали направление от ее центра.
Рис. 34. Исходный объект — стрелка
Рис. 35. В качестве траектории будет использован эллипс
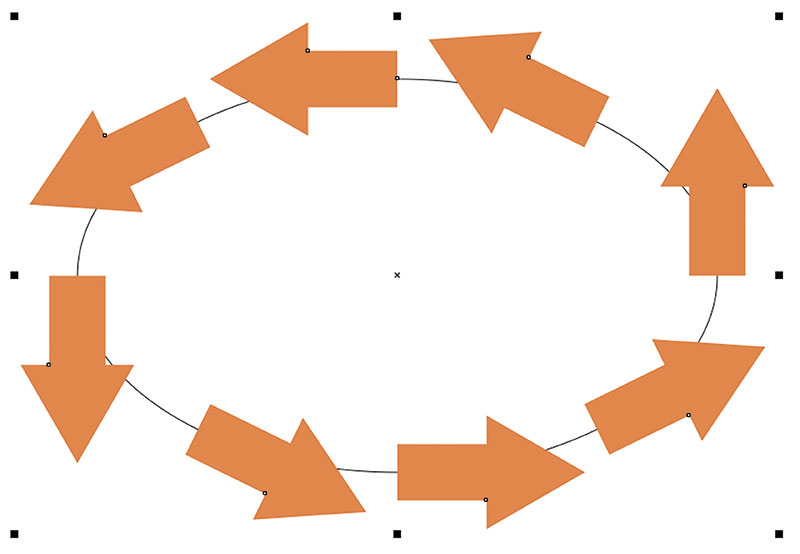
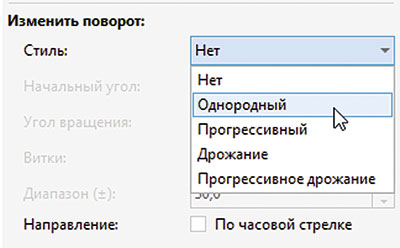
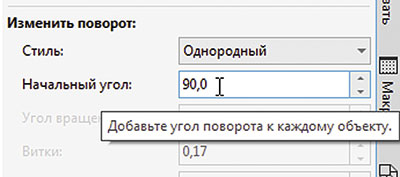
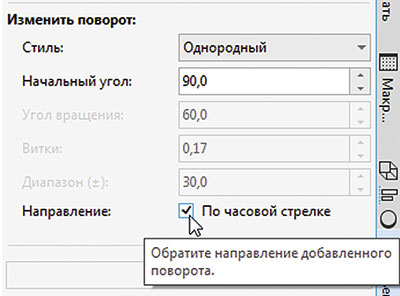
Если включить функцию автоповорота, которую мы уже задействовали в предыдущем примере, то копии исходного объекта будут расположены, как показано на рис. 36. Чтобы достичь желаемого результата, исходный объект необходимо повернуть на 90°. Для этого в разделе Изменить поворот палитры настроек Объекты вдоль пути откройте ниспадающий список Стиль и выберите в нем пункт Однородный (рис. 37). В поле Начальный угол введите значение угла поворота — в данном случае 90° (рис. 38). Поскольку по умолчанию отсчет ведется в направлении против часовой стрелки, включите опцию По часовой стрелке (рис. 39). В поле Дубликат(ы) введите требуемое количество копий и нажмите кнопку Применить в нижней части палитры. Теперь полученный результат соответствует замыслу (рис. 40).
Рис. 36. Результат размещения копий исходного объекта с использованием функции автоповорота
Рис. 37. Выбор нужного варианта поворота исходного объекта в палитре настроек Объекты вдоль пути
Рис. 38. Ввод значения начального угла поворота исходного объекта в палитре настроек Объекты вдоль пути
Рис. 39. Включение опции По часовой стрелке в палитре настроек Объекты вдоль пути
Рис. 40. Теперь копии исходного объекта расположены так, как требовалось
Скорее всего, внимательные читатели уже обратили внимание на то, что в списке Стиль представлено несколько способов автоматического поворота объектов, расположенных вдоль выбранного пути. На рис. 4144 можно визуально сравнить результаты, которые получаются при выборе каждого из вариантов с указанными настройками. Для наглядности объекты располагаются вдоль прямой линии.
Рис. 41. Расположение объектов при выборе режима «однородный» (задан поворот на угол 60°)
Рис. 42. Расположение объектов при выборе режима «прогрессивный»
Рис. 43. Расположение объектов при выборе режима «дрожание»
Рис. 44. Расположение объектов при выборе режима «прогрессивное дрожание»
Видео:ПОЛЕЗНЫЙ УРОК. Как скруглить углы у любого объекта в Корел 2019. Corel DRAWСкачать

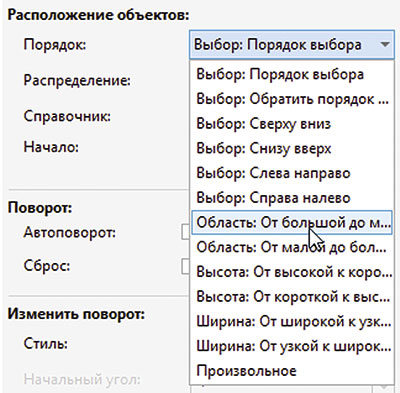
Меняем порядок расположения объектов
Еще одна возможность, реализованная в палитре настроек Объекты вдоль пути — выбор различных вариантов порядка, в котором будут расположены объекты на траектории. Это весьма удобно в том случае, если у вас возникла необходимость упорядочить большое количество исходных объектов различных форм и/или размеров по определенному признаку.
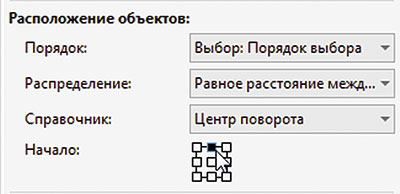
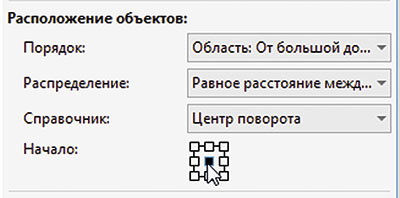
Выбор нужного варианта осуществляется в ниспадающем списке Порядок раздела Расположение объектов палитры Объекты вдоль пути. В качестве признака для сортировки можно выбрать порядок следования исходных объектов в окне документа (слева направо, справа налево, сверху вниз или снизу вверх), последовательность их выделения, площадь (от меньшей к большей или наоборот), ширину или высоту. Кроме того, есть пункт выбора произвольного порядка. Чтобы понять, как это работает, рассмотрим простой пример.
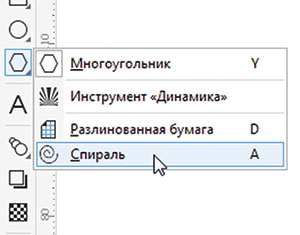
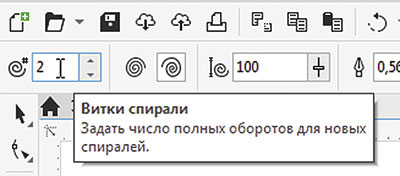
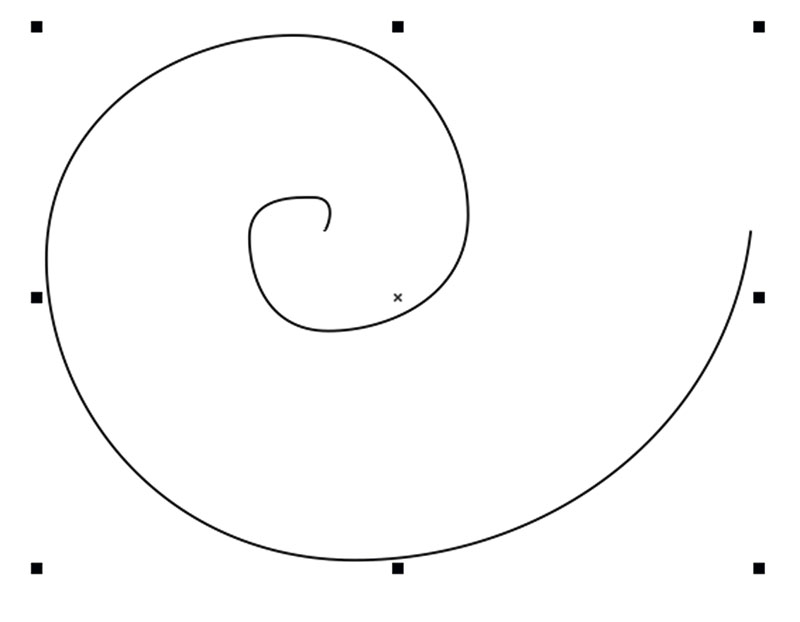
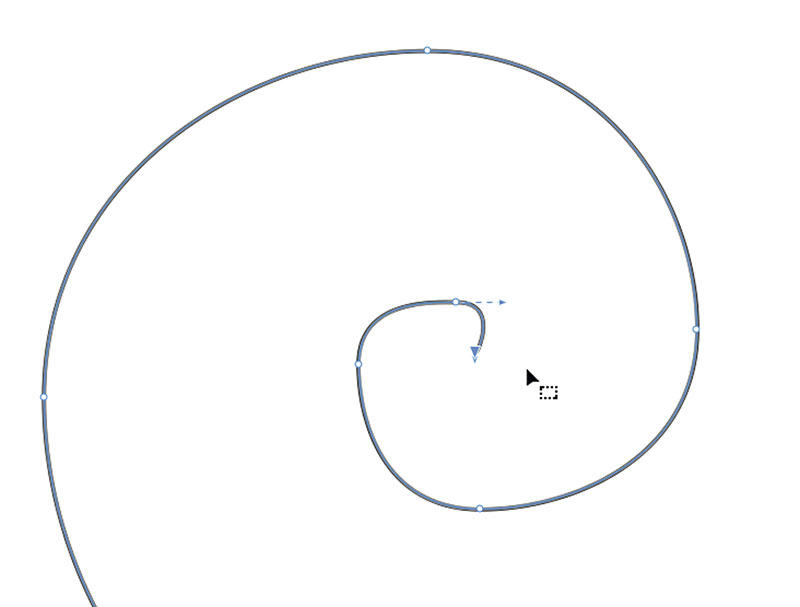
Включите инструмент Спираль (рис. 45). В поле количества витков на панели свойств введите значение «2» (рис. 46). Создайте спираль (рис. 47). Переключитесь на инструмент создания форм (F10), выделите конечную узловую точку (рис. 48) и удалите ее.
Рис. 45. Пиктограмма выбора инструмента Спираль на панели инструментов
Рис. 46. Поле ввода количества витков спирали на панели свойств
Рис. 47. Создание спирали.
Рис. 48. Выделение конечной узловой точки спирали
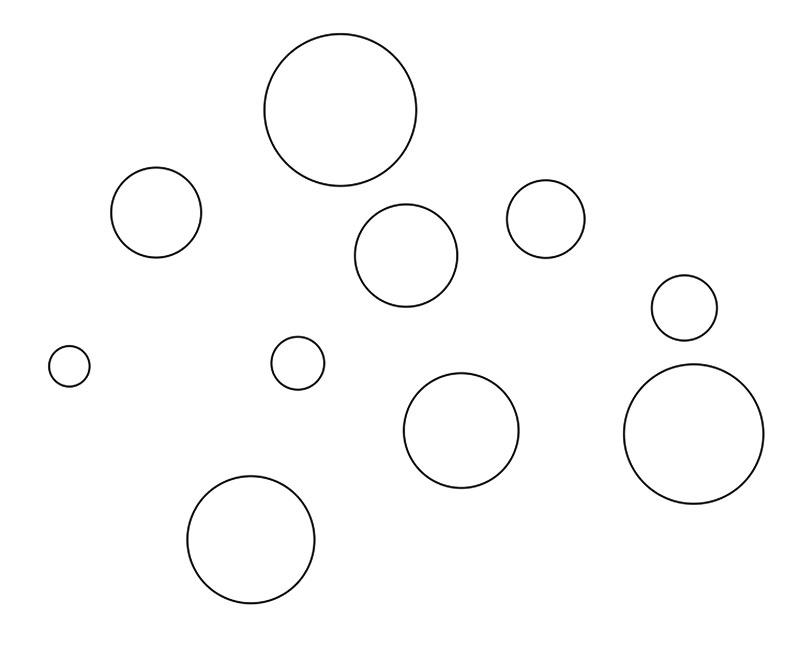
При помощи инструмента Эллипс создайте несколько окружностей различного размера (рис. 49). Задайте для них режим «без абриса» и радиальную градиентную заливку (рис. 50).
Рис. 49. Создание окружностей
Рис. 50. Окружности закрашены градиентной заливкой
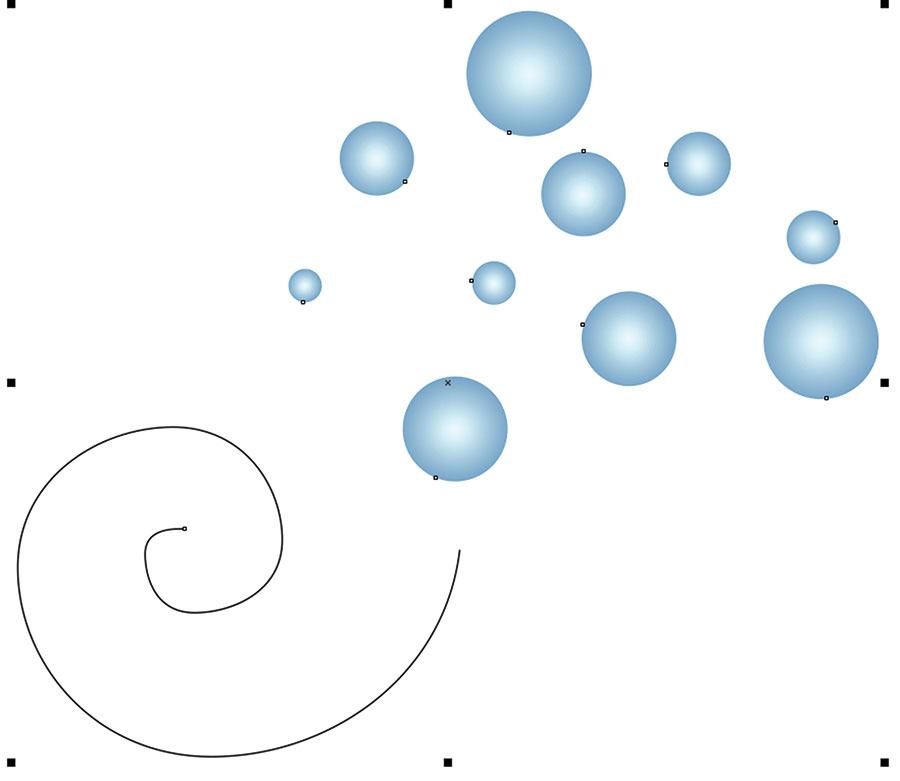
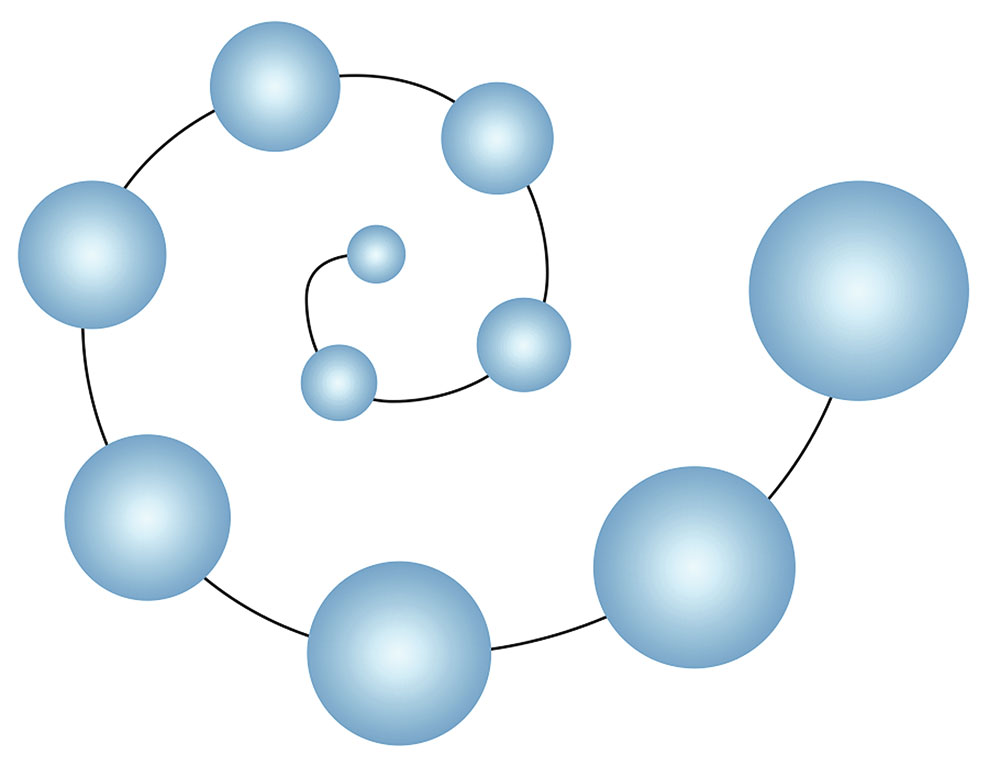
Переключитесь на инструмент выбора, выделите все окружности и ранее созданную спираль (рис. 51). В палитре настроек Объекты вдоль пути отключите опции Сохранить исходные и Следовать пути. В поле Дубликат(ы) введите значение «0». Задайте положение начальной точки по центру (рис. 52). В ниспадающем списке Порядок выберите пункт Область: от большой до малой2 (рис. 53). Нажмите кнопку Применить. Теперь исходные окружности расположены по спирали в порядке увеличения площади (рис. 54).
Рис. 51. Выделение объектов
Рис. 52. Выбор положения начальной точки в палитре настроек Объекты вдоль пути
Рис. 53. Выбор нужного порядка расположения объектов из ниспадающего списка
Рис. 54. Исходные окружности расположены по спирали в порядке увеличения площади
Попробуйте самостоятельно поэкспериментировать, выбирая различные варианты порядка следования объектов и сравнивая полученные результаты.
Видео:ПРОСТЫЕ ФИГУРЫ. ВЫБОР ОБЪЕКТА. CORELСкачать

Заключение
Итак, мы рассмотрели некоторые из множества возможностей, которые предоставляет в распоряжение пользователя графического редактора CorelDRAW функция Объекты вдоль пути. Как вы сможете убедиться на собственном опыте, благодаря большому количеству настроек она не только позволяет расположить объекты по выбранной траектории, но и управлять множеством дополнительных параметров — в частности, углом поворота, порядком следования и др. Используя функцию Объекты вдоль пути, вы сможете сэкономить немало времени, а также получить весьма интересные результаты, экспериментируя с различными вариантами настроек.
1 В предыдущих локализованных версиях CorelDRAW эта палитра называлась Свойства объекта. – Прим. ред.
2 В данном случае стоит поправить огрехи локализации: сортировка осуществляется по площади объектов. – Прим. ред.
📺 Видео
КАК НАРИСОВАТЬ ТРЕУГОЛЬНИК. 7 СПОСОБОВ. Corel DRAW. КОРЕЛ. Уроки для начинающихСкачать

ГЕОМЕТРИЧЕСКИЙ ОРНАМЕНТ НА ОСНОВЕ КРУГА. КОРЕЛ. COREL DRAWСкачать

Corel Draw Уроки | 11. Орнамент по кругуСкачать

Как растянуть узор по кругу или вдоль пути. Corel Draw от ДеревяшкинаСкачать

Топ 5 инструментов для работы в Corel Draw (описание и примеры использования)Скачать

Как залить картинку в фигуру в Corel Draw Просто и БыстроСкачать

КАК НАРИСОВАТЬ КРУГ. Corel DRAW. Уроки корел для начинающихСкачать

Как разместить надпись по кругу в CoreldrawСкачать
CorelDraw. Урок 3. Работаем с текстом в Corel Draw. Простой и фигурный текст в КорелСкачать

Уроки Corel Draw. Орнамент по кругу в Корел.Скачать

 чертится прямая линия и на ней ставится точка;
чертится прямая линия и на ней ставится точка;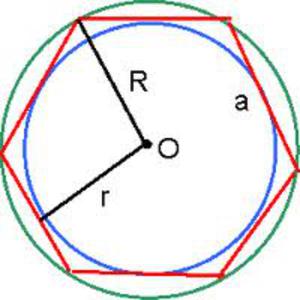 Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.