Вписанные окружности теория егэ профиль (6 видео)

Теория к заданию 6 ЕГЭ профильной математики

ПЛАНИМЕТРИЯ. Центральные и вписанные углы. Касательная, хорда, секущая. Вписанные и описанные окружности (теория к заданию 6 ЕГЭ профильной математики)

Учим и применяем формулы и теоремы.

Автор: Лариса Алькаева. Репетитор по математике

Из материала:

Отрезок, соединяющий две точки на окружности, называется хордой.

Самая большая хорда проходит через центр окружности и называется диаметром.

Центральный угол — угол, вершина которого лежит в центре окружности.

Центральный угол равен дуге, на которую опирается.

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность.

Содержание

Подготовка к ЕГЭ «Вписанные и описанные окружности»
Описанная и вписанная окружность
теория по математике 📈 планиметрия
Описанная окружность
Вписанная окружность
Вписанный и описанный треугольники
Вписанный и описанный четырехугольники
🎦 Видео

Видео:Все об окружностях на ЕГЭ | Профильная математика 2023 | УмскулСкачать

Подготовка к ЕГЭ «Вписанные и описанные окружности»

Вписанные и описанные окружности

Вписанная окружность.

Окружность называется вписанной в многоугольник , если она касается его сторон. Центр вписанной окружности лежит в точке пересечения биссектрис углов многоугольника.

Не во всякий многоугольник можно вписать окружность.

Площадь многоугольника, в который вписана окружность можно найти по формуле ,

здесь — полупериметр многоугольника, — радиус вписанной окружности.

Отсюда радиус вписанной окружности равен

Если в выпуклый четырехугольник вписана окружность, то суммы длин противоположных сторон равны . Обратно: если в выпуклом четырехугольнике суммы длин противоположных сторон равны, то в четырехугольник можно вписать окружность:

В любой треугольник можно вписать окружность, притом только одну. Центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов треугольника.

Радиус вписанной окружности равен . Здесь

Описанная окружность.

Окружность называется описанной около многоугольника , если она проходит через все вершины многоугольника. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров сторон многоугольника. Радиус вычисляется как радиус окружности, описанной около треугольника, определенного любыми тремя вершинами данного многоугольника:

Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна .

∠ + ∠ = ∠ + ∠

Около любого треугольника можно описать окружность, притом только одну. Ее центр лежит в точке пересечения серединных перпендикуляров сторон треугольника:

Радиус описанной окружности вычисляется по формулам:

где — длины сторон треугольника, — его площадь.

Найдите радиус окружности, вписанной в квадрат со стороной 16.

Сторона ромба равна 58, острый угол равен 30˚. Найдите радиус вписанной окружности этого ромба.

Найдите высоту трапеции, в которую вписана окружность радиуса 14.

Периметр прямоугольной трапеции, описанной около окружности, равен 80, ее большая боковая сторона равна 30. Найдите радиус окружности.

В четырехугольник ABCD вписана окружность, AB=52, CD=53. Найдите периметр четырехугольника.

Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1:17:23 . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 84.

Угол A четырехугольника ABCD , вписанного в окружность, равен 26˚. Найдите угол C этого четырехугольника. Ответ дайте в градусах.

Стороны четырехугольника ABCD AB , BC , CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 78˚, 107˚, 39˚, 136˚. Найдите угол C этого четырехугольника. Ответ дайте в градусах.

Точки A , B , C , D , расположенные на окружности, делят эту окружность на четыре дуги AB , BC , CD и AD , градусные величины которых относятся соответственно как 1:2:7:26. Найдите угол A четырехугольника ABCD . Ответ дайте в градусах.

Четырехугольник ABCD вписан в окружность. Угол ABC равен 38˚, угол CAD равен 33˚. Найдите угол ABD . Ответ дайте в градусах.

Меньшая сторона прямоугольника равна 16. Угол между диагоналями равен 60˚. Найдите радиус описанной окружности этого прямоугольника.

Около трапеции описана окружность. Периметр трапеции равен 60, средняя линия равна 25. Найдите боковую сторону трапеции.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60˚, большее основание равно 82. Найдите радиус описанной окружности этой трапеции.

Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

Периметр правильного шестиугольника равен 108. Найдите диаметр описанной окружности.

Видео:Все о вписанных и описанных окружностях с нуля | PARTAСкачать

Описанная и вписанная окружность

теория по математике 📈 планиметрия

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Описанная окружность

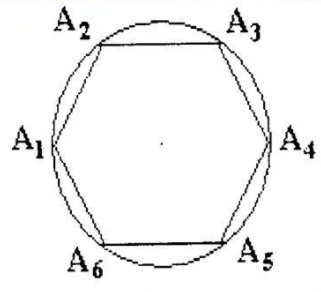
Окружность называется описанной вокруг многоугольника, если все вершины многоугольника принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.

Любой правильный многоугольник можно вписать в окружность. На рисунке описанная окружность проходит через каждую вершину правильного шестиугольника.

Видео:✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Вписанная окружность

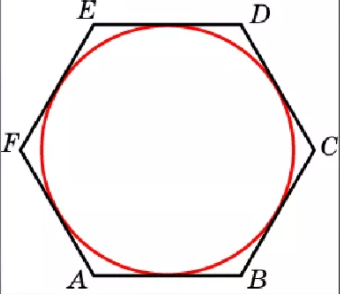
Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в этом случае называется описанным около окружности.

В любой правильный многоугольник можно вписать окружность. На рисунке окружность вписана в правильный шестиугольник, она касается всех его сторон.

Вписанный и описанный треугольники

Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.

В любой треугольник можно вписать окружность: 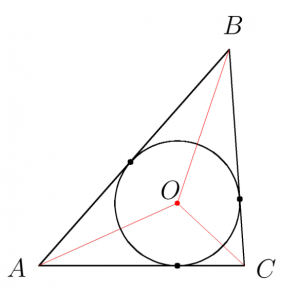Центр вписанной окружности

Центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.

Вписанный и описанный четырехугольники

Не во всякий четырехугольник можно вписать окружность. Например, в прямоугольник нельзя вписать окружность. По рисунку видно, что окружность касается только трех его сторон, что не соответствует определению.

Условие вписанной в 4-х угольник окружности

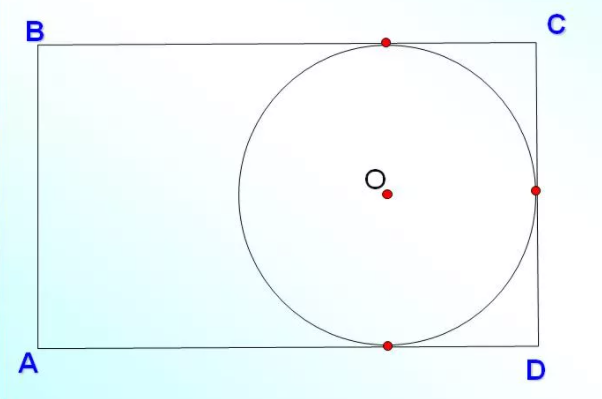
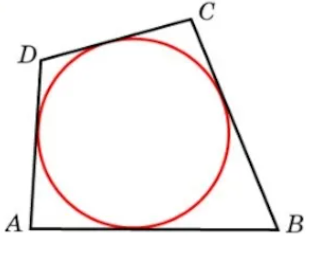
Окружность является вписанной в четырехугольник, если суммы длин противоположных сторон равны.

На рисунке выполняется данное условие, то есть AD + BC=DC + AB

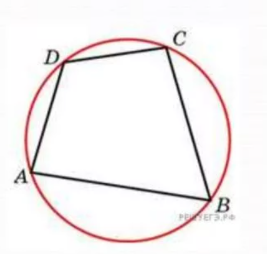
Окружность является описанной около четырехугольника, если суммы противоположных углов равны 180 градусов.

На рисунке окружности описана около четырехугольника, следовательно выполнено условие, что сумма углов А и С равна сумме углов B и D и равна 180 градусов.