Вписанная и описанная окружность 8 класс теория

Определения

Центральный угол – это угол, вершина которого лежит в центре окружности.

Вписанный угол – это угол, вершина которого лежит на окружности.

Градусная мера дуги окружности – это градусная мера центрального угла, который на неё опирается.

Теорема

Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.

Доказательство

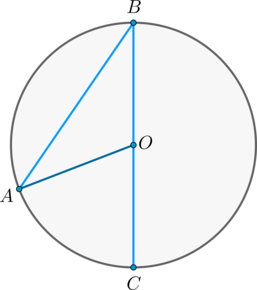
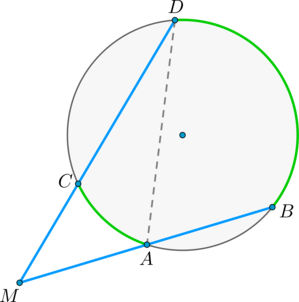
Доказательство проведём в два этапа: сначала докажем справедливость утверждения для случая, когда одна из сторон вписанного угла содержит диаметр. Пусть точка (B) – вершина вписанного угла (ABC) и (BC) – диаметр окружности:

Треугольник (AOB) – равнобедренный, (AO = OB) , (angle AOC) – внешний, тогда (angle AOC = angle OAB + angle ABO = 2angle ABC) , откуда (angle ABC = 0,5cdotangle AOC = 0,5cdotbuildrelsmileover) .

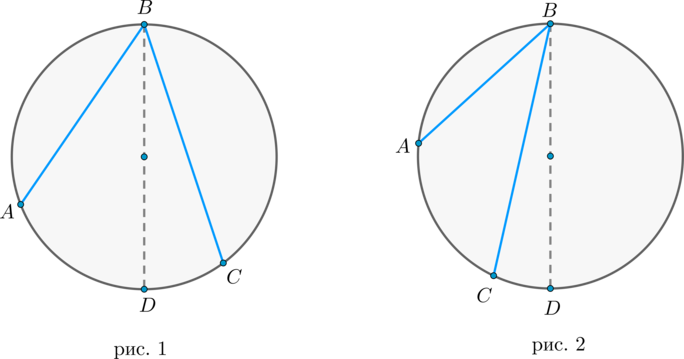
Теперь рассмотрим произвольный вписанный угол (ABC) . Проведём диаметр окружности (BD) из вершины вписанного угла. Возможны два случая:

1) диаметр разрезал угол на два угла (angle ABD, angle CBD) (для каждого из которых теорема верна по доказанному выше, следовательно верна и для исходного угла, который является суммой этих двух и значит равен полусумме дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 1.

2) диаметр не разрезал угол на два угла, тогда у нас появляется ещё два новых вписанных угла (angle ABD, angle CBD) , у которых сторона содержит диаметр, следовательно, для них теорема верна, тогда верна и для исходного угла (который равен разности этих двух углов, значит, равен полуразности дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 2.

Следствия

1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.

2. Вписанный угол, опирающийся на полуокружность, прямой.

3. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.

Определения

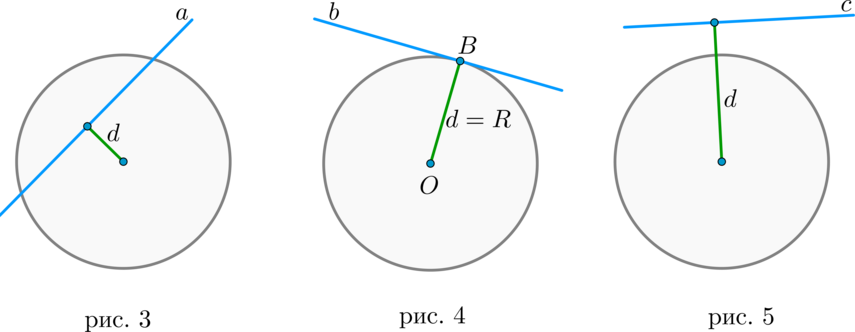
Существует три типа взаимного расположения прямой и окружности:

1) прямая (a) пересекает окружность в двух точках. Такая прямая называется секущей. В этом случае расстояние (d) от центра окружности до прямой меньше радиуса (R) окружности (рис. 3).

2) прямая (b) пересекает окружность в одной точке. Такая прямая называется касательной, а их общая точка (B) – точкой касания. В этом случае (d=R) (рис. 4).

3) прямая (c) не имеет общих точек с окружностью (рис. 5).

Теорема

1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

2. Если прямая проходит через конец радиуса окружности и перпендикулярна этому радиусу, то она является касательной к окружности.

Следствие

Отрезки касательных, проведенных из одной точки к окружности, равны.

Доказательство

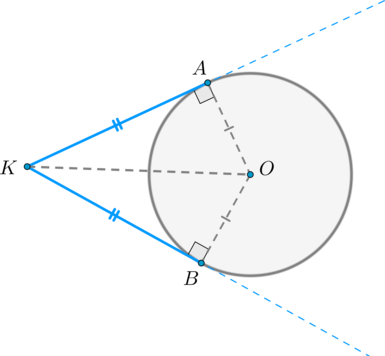
Проведем к окружности из точки (K) две касательные (KA) и (KB) :

Значит, (OAperp KA, OBperp KB) как радиусы. Прямоугольные треугольники (triangle KAO) и (triangle KBO) равны по катету и гипотенузе, следовательно, (KA=KB) .

Следствие

Центр окружности (O) лежит на биссектрисе угла (AKB) , образованного двумя касательными, проведенными из одной точки (K) .

Теорема об угле между секущими

Угол между двумя секущими, проведенными из одной точки, равен полуразности градусных мер большей и меньшей высекаемых ими дуг.

Доказательство

Пусть (M) – точка, из которой проведены две секущие как показано на рисунке:

Покажем, что (angle DMB = dfrac(buildrelsmileover — buildrelsmileover)) .

(angle DAB) – внешний угол треугольника (MAD) , тогда (angle DAB = angle DMB + angle MDA) , откуда (angle DMB = angle DAB — angle MDA) , но углы (angle DAB) и (angle MDA) – вписанные, тогда (angle DMB = angle DAB — angle MDA = fracbuildrelsmileover — fracbuildrelsmileover = frac(buildrelsmileover — buildrelsmileover)) , что и требовалось доказать.

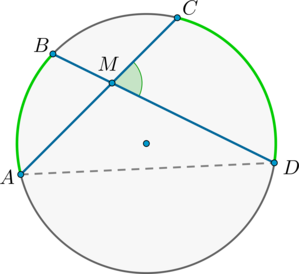
Теорема об угле между пересекающимися хордами

Угол между двумя пересекающимися хордами равен полусумме градусных мер высекаемых ими дуг: [angle CMD=dfrac12left(buildrelsmileover+buildrelsmileoverright)]

Доказательство

(angle BMA = angle CMD) как вертикальные.

Из треугольника (AMD) : (angle AMD = 180^circ — angle BDA — angle CAD = 180^circ — frac12buildrelsmileover — frac12buildrelsmileover) .

Но (angle AMD = 180^circ — angle CMD) , откуда заключаем, что [angle CMD = frac12cdotbuildrelsmileover + frac12cdotbuildrelsmileover = frac12(buildrelsmileover + buildrelsmileover).]

Теорема об угле между хордой и касательной

Угол между касательной и хордой, проходящей через точку касания, равен половине градусной меры дуги, стягиваемой хордой.

Доказательство

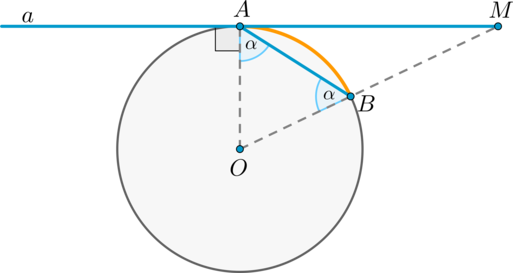
Пусть прямая (a) касается окружности в точке (A) , (AB) – хорда этой окружности, (O) – её центр. Пусть прямая, содержащая (OB) , пересекает (a) в точке (M) . Докажем, что (angle BAM = frac12cdot buildrelsmileover) .

Обозначим (angle OAB = alpha) . Так как (OA) и (OB) – радиусы, то (OA = OB) и (angle OBA = angle OAB = alpha) . Таким образом, (buildrelsmileover = angle AOB = 180^circ — 2alpha = 2(90^circ — alpha)) .

Так как (OA) – радиус, проведённый в точку касания, то (OAperp a) , то есть (angle OAM = 90^circ) , следовательно, (angle BAM = 90^circ — angle OAB = 90^circ — alpha = frac12cdotbuildrelsmileover) .

Теорема о дугах, стягиваемых равными хордами

Равные хорды стягивают равные дуги, меньшие полуокружности.

И наоборот: равные дуги стягиваются равными хордами.

Доказательство

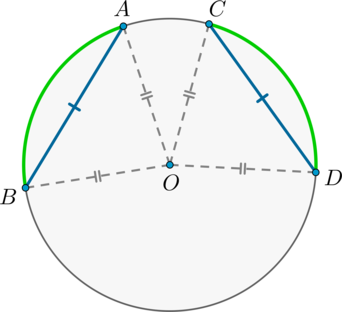
1) Пусть (AB=CD) . Докажем, что меньшие полуокружности дуги (buildrelsmileover=buildrelsmileover) .

(triangle AOB=triangle COD) по трем сторонам, следовательно, (angle AOB=angle COD) . Но т.к. (angle AOB, angle COD) — центральные углы, опирающиеся на дуги (buildrelsmileover, buildrelsmileover) соответственно, то (buildrelsmileover=buildrelsmileover) .

2) Если (buildrelsmileover=buildrelsmileover) , то (triangle AOB=triangle COD) по двум сторонам (AO=BO=CO=DO) и углу между ними (angle AOB=angle COD) . Следовательно, и (AB=CD) .

Теорема

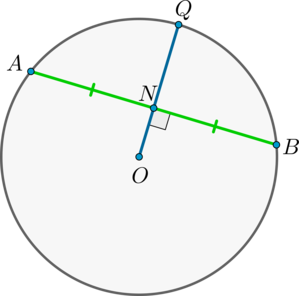
Если радиус делит хорду пополам, то он ей перпендикулярен.

Верно и обратное: если радиус перпендикулярен хорде, то точкой пересечения он делит ее пополам.

Доказательство

1) Пусть (AN=NB) . Докажем, что (OQperp AB) .

Рассмотрим (triangle AOB) : он равнобедренный, т.к. (OA=OB) – радиусы окружности. Т.к. (ON) – медиана, проведенная к основанию, то она также является и высотой, следовательно, (ONperp AB) .

2) Пусть (OQperp AB) . Докажем, что (AN=NB) .

Аналогично (triangle AOB) – равнобедренный, (ON) – высота, следовательно, (ON) – медиана. Следовательно, (AN=NB) .

Теорема о произведении отрезков хорд

Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

Доказательство

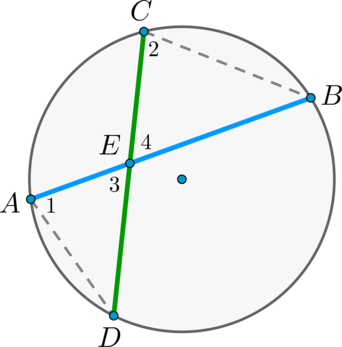
Пусть хорды (AB) и (CD) пересекаются в точке (E) .

Рассмотрим треугольники (ADE) и (CBE) . В этих треугольниках углы (1) и (2) равны, так как они вписанные и опираются на одну и ту же дугу (BD) , а углы (3) и (4) равны как вертикальные. Треугольники (ADE) и (CBE) подобны (по первому признаку подобия треугольников).

Тогда (dfrac = dfrac) , откуда (AEcdot BE = CEcdot DE) .

Теорема о касательной и секущей

Квадрат отрезка касательной равен произведению секущей на ее внешнюю часть.

Доказательство

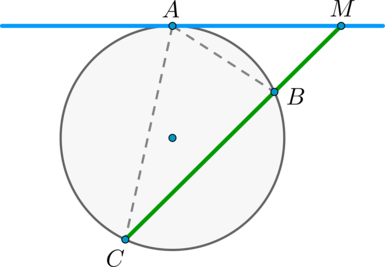
Пусть касательная проходит через точку (M) и касается окружности в точке (A) . Пусть секущая проходит через точку (M) и пересекает окружность в точках (B) и (C) так что (MB . Покажем, что (MBcdot MC = MA^2) .

Рассмотрим треугольники (MBA) и (MCA) : (angle M) – общий, (angle BCA = 0,5cdotbuildrelsmileover) . По теореме об угле между касательной и секущей, (angle BAM = 0,5cdotbuildrelsmileover = angle BCA) . Таким образом, треугольники (MBA) и (MCA) подобны по двум углам.

Из подобия треугольников (MBA) и (MCA) имеем: (dfrac = dfrac) , что равносильно (MBcdot MC = MA^2) .

Следствие

Произведение секущей, проведённой из точки (O) , на её внешнюю часть не зависит от выбора секущей, проведённой из точки (O) :

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Описанная и вписанная окружность

теория по математике 📈 планиметрия

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Описанная окружность

Окружность называется описанной вокруг многоугольника, если все вершины многоугольника принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.

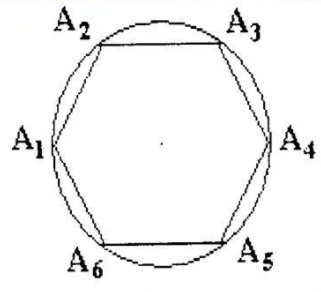
Любой правильный многоугольник можно вписать в окружность. На рисунке описанная окружность проходит через каждую вершину правильного шестиугольника.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Вписанная окружность

Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в этом случае называется описанным около окружности.

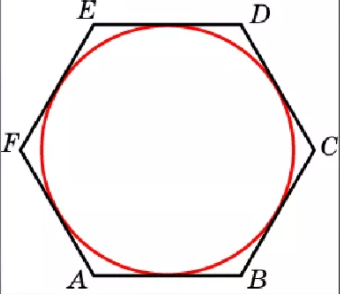
В любой правильный многоугольник можно вписать окружность. На рисунке окружность вписана в правильный шестиугольник, она касается всех его сторон.

Вписанный и описанный треугольники

Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.

В любой треугольник можно вписать окружность: 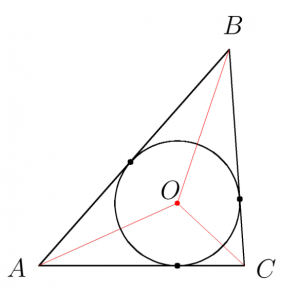Центр вписанной окружности

Центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.

Вписанный и описанный четырехугольники

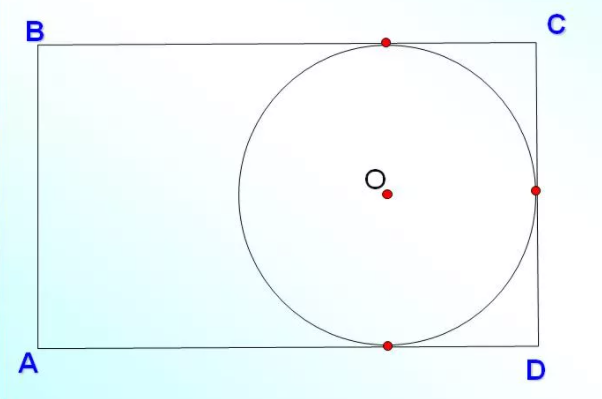
Не во всякий четырехугольник можно вписать окружность. Например, в прямоугольник нельзя вписать окружность. По рисунку видно, что окружность касается только трех его сторон, что не соответствует определению.

Условие вписанной в 4-х угольник окружности

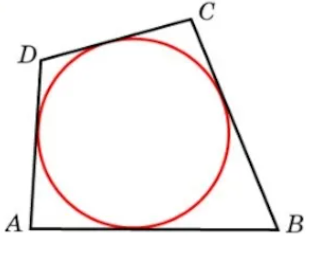
Окружность является вписанной в четырехугольник, если суммы длин противоположных сторон равны.

На рисунке выполняется данное условие, то есть AD + BC=DC + AB

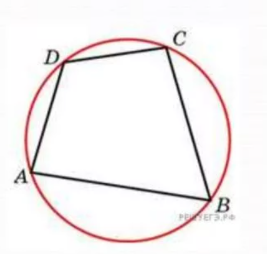
Окружность является описанной около четырехугольника, если суммы противоположных углов равны 180 градусов.

На рисунке окружности описана около четырехугольника, следовательно выполнено условие, что сумма углов А и С равна сумме углов B и D и равна 180 градусов.

Видео:Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

Презентация по геометрии в 8 классе на тему «Вписанные и описанные окружности»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

D В С Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник. А E А многоугольник называется описанным около этой окружности.

D В С Какой из двух четырехугольников АВСD или АЕКD является описанным? А E К

D В С В прямоугольник нельзя вписать окружность. А

D В С Какие известные свойства нам пригодятся при изучении вписанной окружности? А E Свойство касательной Свойство отрезков касательных F P

D В С В любом описанном четырехугольнике суммы противоположных сторон равны. А E R N F

D В С Сумма двух противоположных сторон описанного четырехугольника равна 15 см. Найдите периметр этого четырехугольника. А № 695 ВC+AD=15 AB+DC=15 PABCD = 30 см

D F Найти FD А N ? 4 7 6 5

D В С Равнобокая трапеция описана около окружности. Основания трапеции равны 2 и 8. найдите радиус вписанной окружности. А ВC+AD=10 AB+DC=10 2 8 2 4

D В С Верно и обратное утверждение. А Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность. ВС + АD = АВ + DC

D В С Можно ли в данный четырехугольник вписать окружность? А 5 + 7 = 4 + 8 5 7 4 8

В С А В любой треугольник можно вписать окружность. Теорема Доказать, что в треугольник можно вписать окружность

В С А 1) ДП: биссектрисы углов треугольника Проведем из точки О перпендикуляры к сторонам треугольника

В С А В любой треугольник можно вписать окружность. Теорема

D В С Докажите, что площадь описанного многоугольника равна половине произведения его периметра на радиус вписанной окружности. А № 697 F a1 a2 a3 … К

D В С Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника. А E А многоугольник называется вписанным в эту окружность.

D В С Какой из многоугольников, изображенных на рисунке является вписанным в окружность? А E L P X E

А В D С Какие известные свойства нам пригодятся при изучении описанной окружности? Теорема о вписанном угле

А В D В любом вписанном четырехугольнике сумма противоположных углов равна 1800. С 3600

? 590 ? 900 ? 650 ? 1000 D А В С 800 1150 D А В С 1210 Найти неизвестные углы четырехугольников.

D Верно и обратное утверждение. Если сумма противоположных углов четырехугольника равна 1800, то около него можно вписать окружность. А В С 800 1000 1130 670

В С А Около любого треугольника можно описать окружность. Теорема Доказать, что можно описать окружность

В С А 1) ДП: серединные перпендикуляры к сторонам 4) ВО=СО=АО, т.е. точка О равноудалена от вершин треугольника. Значит, окружность с центром в т.О и радиусом ОА пройдет через все три вершины треугольника, т.е. является описанной окружностью.

В С А Около любого треугольника можно описать окружность. Теорема

О В С А №702 В окружность вписан треугольник АВС так, что АВ – диаметр окружности. Найдите углы треугольника, если: а) ВС = 1340 1340 670 230 700 550 350

О В С А №703 В окружность вписан равнобедренный треугольник АВС с основанием ВС. Найдите углы треугольника, если ВС = 1020. 1020 510 (1800 – 510) : 2 = 1290 : 2 = 128060/ : 2 = 64030/

В С А №704 (a) Окружность с центром О описана около прямоугольного треугольника. Докажите, что точка О – середина гипотенузы. 1800 д и а м е т р

В С А №704 (б) Окружность с центром О описана около прямоугольного треугольника. Найдите стороны треугольника, если диаметр окружности равен d, а один из острых углов треугольника равен . d

С В А №705 (а) Около прямоугольного треугольника АВС с прямым углом С описана окружность. Найдите радиус этой окружности, если АС=8 см, ВС=6 см. 8 6

С А В №705(б) Около прямоугольного треугольника АВС с прямым углом С описана окружность. Найдите радиус этой окружности, если АС=18 см, 18 300

О В С А Боковые стороны треугольника, изображенного на рисунке, равны 3 см. Найти радиус описанной около него окружности. 1800 3 3

О В С А Радиус окружности, описанной около треугольника, изображенного на чертеже, равен 2 см. Найти сторону АВ. 1800 2 2 450 ?

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 931 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 67 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 682 человека из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 494 849 материалов в базе

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Дистанционные курсы для педагогов

Другие материалы

• 13.04.2020
• 233

• 13.04.2020
• 840

• 13.04.2020
• 100

• 13.04.2020
• 124

• 13.04.2020
• 884

• 13.04.2020
• 149

• 13.04.2020
• 305

• 13.04.2020
• 187

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 13.04.2020 1516 —> —> —> —>
• PPTX 2.1 мбайт —> —>
• Рейтинг: 4 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Филиппова Татьяна Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 4 месяца
• Подписчики: 0
• Всего просмотров: 130937
• Всего материалов: 293

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:8 класс, 38 урок, Вписанная окружностьСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Орловские школы переведут на дистанционное обучение с 24 января

Время чтения: 1 минута

Санкт-Петербургский госуниверситет переходит на дистанционное обучение

Время чтения: 1 минута

Более 800 вузов проведут прием через суперсервис

Время чтения: 1 минута

Число иностранных студентов в РФ увеличилось за три года

Время чтения: 1 минута

В школьном курсе мировой истории планируют уделить больше внимания Азии и Африке

Время чтения: 1 минута

WWF выпустил настольную игру об изменении климата

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📸 Видео

МЕРЗЛЯК-8 ГЕОМЕТРИЯ. ОПИСАННАЯ И ВПИСАННАЯ ОКРУЖНОСТИ ЧЕТЫРЁХУГОЛЬНИКА. ПАРАГРАФ-10. ТЕОРИЯСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Урок по теме ОПИСАННАЯ ОКРУЖНОСТЬ 8 классСкачать

Геометрия 8 класс (Урок№33 - Описанная окружность.)Скачать

Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать

8 класс, 39 урок, Описанная окружностьСкачать

ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

8 класс - Геометрия - Вписанная и описанная окружностиСкачать

Урок по теме ВПИСАННАЯ ОКРУЖНОСТЬСкачать

8 класс Геометрия Вписанные и описанные окружности (теория)Скачать

Вписанная окружность. Видеоурок по геометрии 8 классСкачать