Приведите к истинности выражение: Во всяком четырехугольнике диагонали одинаковы. Если это выражение является ложным
- Шагалиева Кира
- Математика 2019-09-24 11:08:27 1 1
Ответ: Ошибочно, что во всяком четырёхугольнике диагонали одинаковы.
Объяснение: Если к ошибочному высказыванию добавить слова «Ошибочно, что», то это выражение станет правильным. А если к правильному высказыванию добавить слова «Ошибочно, что», то это выражение станет ложным.
Видео:Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать
Во всяком четырехугольнике диагонали равны истина
Высказывание – основное понятие математической логики
Высказывание – предложение, которое либо истинно либо ложно
1. Новгород стоит на Волхове
2. Карась не рыба
3. Антананариву – столица Мадагаскара
4. Волга впадает в Чёрное море
5. Найдётся целое число х, удовлетворяющее соотношению х 2 =0
6. Существует простое чётное число
Высказывания 1,3, 6 истинны (для 6 ответ 2), а 2, 4 и 5 ложны
В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, а от их житейского содержания отвлекаются.
Утверждения, которые кажутся истинными, а на самом деле ложные – парадоксы
Это предложение содержит 6 слов – ложь. Значит, противоположное предложение должно быть истинным:
Это предложение не содержит 6 слов
Но это снова ложь!
Восклицательные и вопросительные предложения не могут быть высказываниями.
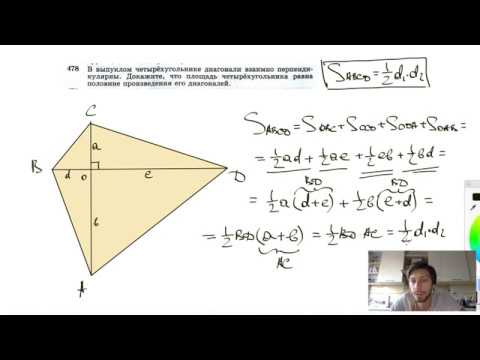
Видео:№478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадьСкачать
Виды теорем
Рассмотрим, например, теорему «если четырехугольник является прямоугольником, то в нем диагонали равны». Построим предложение, обратное данному: «если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником». Это ложное высказывание, в чем легко убедиться (в равнобедренной трапеции диагонали равны, но трапеция не является прямоугольником).
Рассмотрим теорему «в равнобедренном треугольнике углы при основании равны». Обратное ей предложение таково: «если в треугольнике углы при основании равны, то этот треугольник – равнобедренный». Это истинное предложение и потому является теоремой. Ее называют теоремой, обратной данной.
Для любой теоремы вида А
В (если А, то В) можно сформулировать предложение 
(если не А, то не В), которое называют противоположным данному. Но это предложение также не всегда является теоремой. Например, предложение, противоположное теореме «если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником» будет ложным: «если четырехугольник не является прямоугольником, то в нем диагонали не равны».
В том случае, если предложение, противоположное данному, будет истинно, его называют теоремой, противоположной данной.
Для всякой теоремы вида А
В (если А, то В) можно сформулировать предложение 
(если не В, то не А), которое называют обратным противоположному. Например, для теоремы «если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником» предложение, обратное противоположному, будет таким: «если в четырехугольнике диагонали не равны, то он не является прямоугольником». Это, как известно, предложение истинное, и, следовательно, является теоремой, обратно противоположной данной.
Вообще, для какой бы теоремы мы ни формулировали предложение, обратное противоположному, оно всегда будет теоремой, потому что имеется следующая равносильность: ( А
В) 
(
).
Эту равносильность называют законом контрапозиции.
Теоремы А
В и В
А – взаимообратные, а А
В и 
– взаимопротивоположные.
1. В следующих теоремах выделим условие и заключение: а) «Для того чтобы разность двух чисел делилась на 2, достаточно, чтобы на 2 делилось уменьшаемое и вычитаемое»;
б) «Для того чтобы четырехугольник был квадратом, необходимо, чтобы хоты бы один из его углов был прямым».
Решение: а) Слово достаточно относится к предложению «уменьшаемое и вычитаемое делится на 2», следовательно, это предложение и является условием теоремы. Тогда заключение теоремы – «разность двух чисел делится на 2».
б) В данной теореме есть слово «необходимо», которое относится к предложению «чтобы четырехугольник был квадратом». Значит, это и будет условием данной теоремы. А ее заключением в таком случае будет предложение «один из углов четырехугольника прямой».
2. Сформулируем следующие теоремы в виде «если …, то …»:
а) «Перпендикуляр к одной из двух параллельных прямых также перпендикуляр к другой»; б) «Всякий параллелограмм имеет центр симметрии».
Решение: а) Выделим условие и заключение теоремы: «Перпендикуляр к одной из двух параллельных прямых» – условие, «перпендикуляр к другой» – заключение. Тогда теорема примет вид: «Если есть перпендикуляр к одной из двух параллельных прямых, то он является также перпендикуляром к другой прямой».
б) Условие теоремы – «всякий параллелограмм», заключение – «имеет центр симметрии». Нашу теорему тогда можно переформулировать следующим образом: «Если фигура параллелограмм, то она имеет центр симметрии».
3. Дана теорема: «Если в четырехугольнике две противоположные стороны равны и параллельны, то четырехугольник параллелограмм». Сформулируем предложения, являющиеся обратным, противоположным и обратно противоположным.
Решение: Выделим условие и заключение данной теоремы. Условие: «в четырехугольнике две противоположные стороны равны и параллельны». Заключение: «четырехугольник – параллелограмм».
Поменяв местами условие и заключение, получим теорему, обратную данной: «Если четырехугольник – параллелограмм, то две противоположные стороны равны и параллельны», так как данное предложение истинно.
Заменяя условие и заключение исходной теоремы их отрицаниями, получим теорему, противоположную данной: «Если в четырехугольнике две противоположные стороны не равны или не параллельны, то четырехугольник – не параллелограмм». Это предложение также истинно.
Меняя местами отрицание условия и отрицание заключения, получим истинное предложение, которое является обратно противоположной теоремой: «Если четырехугольник – не параллелограмм, то две противоположные стороны не равны или не параллельны».
🌟 Видео
№410. Является ли четырехугольник квадратом, если его диагонали: а) равны и взаимноСкачать
Доказательство первого признака параллелограммаСкачать
Школково. Вебинар 3. Разбор четырех задач №16 из ЕГЭ по математикеСкачать
№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать
Чему равна сумма углов выпуклого многоугольникаСкачать
Диалог с Денисом Сенниковым. "Четыре экзистенциальные данности, четыре благородные истины" 2 встречаСкачать
Георгий Челпанов. Учебник логики. Главы 1-26 (Книга полностью)Скачать
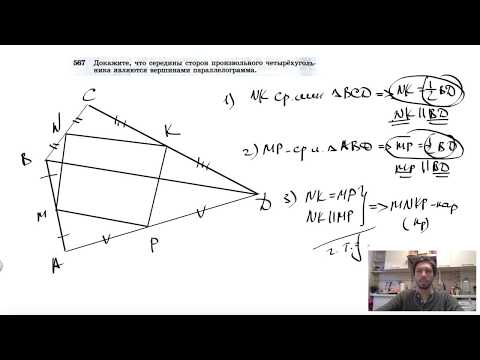
№567. Докажите, что середины сторон произвольного четырехугольника являютсяСкачать
Симедиана. Гармонические четырехугольники. | Олимпиадная математикаСкачать
№950. Докажите, что четырехугольник MNPQ является параллелограммом,Скачать
ДУДОСИМ ЯЩЕНКОСкачать
№407. Найдите углы, которые образуют диагонали ромба с его сторонами, если одинСкачать
Подготовка к ОГЭ. Пропорциональные отрезкиСкачать
Классическая концепция истинностиСкачать
№175. Докажите, что если все ребра тетраэдра равны, то все его двугранные углы также равны.Скачать
Параллелограмм | Свойства и признаки параллелограммаСкачать
№1021. Докажите, что площадь параллелограмма равна произведению двух его смежныхСкачать
ОГЭ вариант-8 #8Скачать
