Общие касательные к двум окружностям
 Взаимное расположение двух окружностей Взаимное расположение двух окружностей |
 Общие касательные к двум окружностям Общие касательные к двум окружностям |
 Формулы для длин общих касательных и общей хорды Формулы для длин общих касательных и общей хорды |
 Доказательства формул для длин общих касательных и общей хорды Доказательства формул для длин общих касательных и общей хорды |
Видео:Внутренняя касательная к двум окружностямСкачать

Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
 | ||
| Внешнее касание двух окружностей | ||
 | ||
| Внутреннее касание двух окружностей | ||
 | ||
| Окружности пересекаются в двух точках | ||
 | ||
 | ||
| Каждая из окружностей лежит вне другой | ||
 Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
 Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
 Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
 | |
| Внутреннее касание двух окружностей | |
 | |
| Окружности пересекаются в двух точках | |
 | |
| Внешнее касание двух окружностей | |
 | |
 | |
| Каждая из окружностей лежит вне другой | |
 | |
| Внешняя касательная к двум окружностям | |||||||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||||||
| Внутреннее касание двух окружностей | |||||||||||||||||||||
| Окружности пересекаются в двух точках | |||||||||||||||||||||
| Внешнее касание двух окружностей | |||||||||||||||||||||
| Каждая из окружностей лежит вне другой | |||||||||||||||||||||
| Фигура | Рисунок | Формула | ||||||||||||
| Внешняя касательная к двум окружностям |  | |||||||||||||
| Внутренняя касательная к двум окружностям |  | |||||||||||||
| Общая хорда двух пересекающихся окружностей |  | |||||||||||||
| Внешняя касательная к двум окружностям | ||||
 | ||||
| Внутренняя касательная к двум окружностям | ||||
 | ||||
| Общая хорда двух пересекающихся окружностей | ||||
 | ||||
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
 Длина общей хорды двух окружностей вычисляется по формуле Видео:Внешняя касательная к двум окружностямСкачать 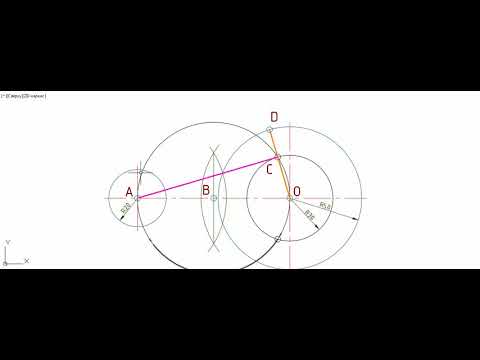 Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Построение общей касательной к двум окружностямСкачать  Построение общей внутренней касательной к двум окружностямДаны две окружности (а это значит, что даны и их центры O1 и O2). Требуется провести общую внутреннюю касательную к ним, то есть такую касательную, от которой данные окружности лежат по разные стороны. Радиус большей окружности называем R, радиус меньшей окружности — r. Сначала вокруг меньшей окружности построим вспомогательную окружность с тем же центром и с радиусом, равным сумме радиусов двух данных окружностей (R + r). Затем построим из центра большей окружности вспомогательную касательную к вспомогательной окружности. Требуемая внутренняя касательная будет параллельна вспомогательной касательной. Отложим первый вспомогательный луч с началом в точке A. Замерим циркулем радиус большей окружности, и тем же раствором циркуля от начала первого луча отложим отрезок AB, равный R. Теперь циркулем замерим радиус меньшей окружности, и тем же раствором циркуля от точки B отложим отрезок BC, равный r. Получился отрезок AC, равный сумме радиусов двух данных окружностей (R + r). Замерим AC циркулем, и тем же раствором циркуля построим первую вспомогательную окружность с центром в O1. Теперь соединим отрезком центры O1 и O2. Произвольным раствором циркуля строим вторую вспомогательную дугу окружности с центром O1. И тем же раствором циркуля строим третью вспомогательную дугу окружности с центром O2 — так, чтобы третья дуга пересекала вторую в двух точках (называем их D и E). Соединяем D и E отрезком, который пересекает O1O2 в середине — эту точку называем F. Теперь замерим циркулем FO1 и этим раствором циркуля строим четвёртую вспомогательную окружность с центром в F на отрезке O1O2, как на диаметре. Эта четвёртая окружность пересекает первую вспомогательную окружность в двух точках (называем их G и H). Выбираем из этих двух точек ту, которая нам больше нравится (в данном построении это точка H), и соединяем прямой с точкой O2. Прямая HO2 — это касательная к первой вспомогательной окружности, проходящая через центр большой данной окружности. Прямая HO2 пересекла большую окружность в двух точках (называем их K и L). Эти точки равно отстоят от O2 и помогут нам построить перпендикуляр к HO2. Произвольным раствором циркуля проводим пятую вспомогательную дугу окружности с центром в K. Тем же раствором циркуля проводим шестую вспомогательную дугу окружности с центром в L — так, чтоб шестая дуга пересекала пятую в некоторой точке (называем точку M). Соединяем O2 и M прямой — эта прямая (перпендикуляр к HO2) пересекает большую данную окружность в некоторой точке (называем её N). Теперь через N проведём прямую, параллельную вспомогательной касательной HO2. Произвольным раствором циркуля строим седьмую вспомогательную окружность с центром в точке N — так, чтоб седьмая окружность пересекала HO2 в двух точках (точки называем P и Q). Тем же раствором циркуля строим восьмую вспомогательную окружность с центром в Q, и восьмая окружность пересекает вспомогательную касательную HO2 в двух точках (точки называем Z и S). Тем же раствором циркуля проводим девятую вспомогательную дугу окружности с центром в S — так, чтобы девятая дуга пересекала седьмую окружность в некоторой точке (точку называем T). Соединяем N и Т прямой — эта прямая NT и будет требуемой общей внутренней касательной к двум данным окружностям. И вот почему. NT проходит через конец радиуса O2N, лежащий на окружности. Также по построению NT параллельна HO2 и перпендикулярна радиусу O2N — следовательно, NT — касательная к большой данной окружности. Теперь проведём радиус O1H и точку его пересечения с прямой TN называем U. Радиус O1H перпендикулярен касательной O2H — значит, угол O2HU — прямой. Получилось, что в четырёхугольнике UHO2N есть три прямых угла — значит, и четвёртый угол HUN прямой, и UHO2N — прямоугольник, в котором сторона HU равна противоположной стороне O2N, то есть радиусу R. Теперь можем найти длину отрезка O1U (составляющего вместе с UH отрезок O1H). Длина равна разности длин O1H и HU, то есть (r + R) — R = r. Выходит, что U отстоит от O1 на r, то есть U лежит на меньшей данной окружности, а это значит, что TN, проходящая через U — проходит через конец радиуса O1U, лежащий на окружности, и перпендикулярна радиусу, то есть TN — касательная к меньшей данной окружности. Построение закончено. Видео:Построение общей внутренней касательной к двум окружностямСкачать  Общие касательныеВыясним сколько общих касательных имеют две окружности и как эти общие касательные могут быть расположены. Если две окружности не пересекаются и окружность меньшего радиуса лежит внутри окружности большего радиуса, то они не имеют общих касательных. В другом случае не пересекающиеся окружности имеют четыре общие касательные. внешние общие касательные При этом, если обе окружности лежат по одну сторону от касательной (в одной полуплоскости), то такая касательная называется внешней. внутренние общие касательные Если окружности лежат по разные стороны от общей касательной (в разных полуплоскостях), то такая касательная называется внутренней. Если две окружности имеют внутреннее касание, то у них есть одна общая касательная. При внешнем касании две окружности имеют три общие касательные. Две пересекающиеся окружности имеют две общие касательные. 🎬 ВидеоПостроение касательной двум окружностям внешнего касанияСкачать  Касательные к двум окружностям.Скачать  Построение внутренней касательной к двум дугам окружностей.Урок12.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать  Построение общей внешней касательной к двум окружностямСкачать  Построение общей касательной к двум окружностямСкачать  Касательная к двум окружностям разного диаметра.Скачать  К двум окружностям проведены общие касательныеСкачать  Построение внешней касательной к двум дугам окружностей. Урок11.(Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать  Пара касающихся окружностей | Осторожно, спойлер! | Борис Трушин |Скачать  Задача 25 ОГЭ Математика 1 ЯщенкоСкачать  Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  Касательная к двум окружностям разного диаметра.2 часть.Скачать  Построение общей касательной к двум окружностямСкачать  №675. Стороны угла О касаются каждой из двух окружностей, имеющих общую касательную в точке АСкачать 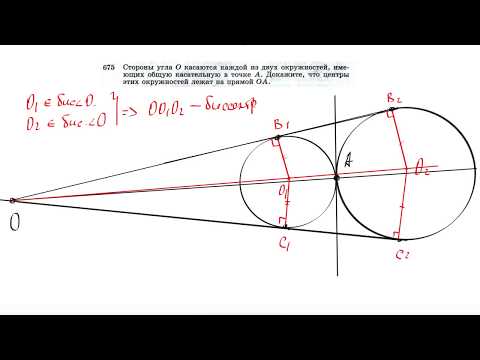 8 класс, 32 урок, Касательная к окружностиСкачать  |
































