Смежные углы всегда равны любой прямоугольник можно вписать окружность

Видео:Смежные углы. 7 класс.Скачать

Смежные углы всегда равны любой прямоугольник можно вписать окружность

Какое из следующих утверждений верно?

1) Любой прямоугольник можно вписать в окружность.

2) Все углы ромба равны.

3) Треугольник со сторонами 1, 2, 4 существует.

Проверим каждое из утверждений.

1) « Любой прямоугольник можно вписать в окружность.» — верно, выпуклый четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположныхх углов этого четырёхугольника равна 180°.

2) «Все углы ромба равны.» — неверно, противоположные углы ромба равны.

3) «Треугольник со сторонами 1, 2, 4 существует.» — неверно, для того, чтобы существовал треугольник, сумма любых его двух сторон должна быть больше третьей стороны.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Задание №19 ОГЭ по математике

В 19 задании из приведенных утверждений необходимо выбрать одно или несколько правильных. Утверждения из общего теоретического курса геометрии, поэтому, какие-то определенные рекомендации здесь дать нельзя, кроме как полного повторения теоретического курса. Другое дело, что если вы точно не знаете какое-либо утверждение, то решить задачу можно наоборот — выбирая и отсеивая неправильные.

Какие из следующих утверждений верны?

1. Все диаметры окружности равны между собой.
2. Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
3. Любые два равносторонних треугольника подобны.

Все диаметры окружности всегда равны между собой — это даже интуитивно понятно. Что касается второго утверждения, то оно неверно — вписанный угол всегда в два раза меньше центрального. А вот третье утверждение тоже верно — треугольники могут быть подобны по трем углам, а у равносторонних треугольников они всегда равны.

pазбирался: Даниил Романович | обсудить разбор | оценить

Какие из следующих утверждений верны?

1. Все высоты равностороннего треугольники равны.
2. Существуют три прямые, которые проходят через одну точку.
3. Если диагонали параллелограмма равны, то он является ромбом.

Первое утверждение верно, так как у равностороннего треугольника все стороны равнозначны, а значит и все элементы, проведенные к ним, тоже. Второе утверждение тоже верно, так как нет ограничений на количество произвольных прямых, проходящих через одну точку. Третье утверждение неверно — если диагонали равны, то это либо прямоугольник, либо квадрат.

pазбирался: Даниил Романович | обсудить разбор | оценить

Какие из следующих утверждений верны?

1. Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
2. Любой прямоугольник можно вписать в окружность.
3. Через заданную точку плоскости можно провести единственную прямую.

Первое утверждение верно из общих свойств треугольника — сумма двух сторон всегда больше третьей. Второе утверждение тоже верно — действительно, любой прямоугольник можно вписать в окружность. Третье утверждение неверно, так как я писал уже чуть выше, что нет ограничений на количество произвольных прямых, проходящих через одну точку.

pазбирался: Даниил Романович | обсудить разбор | оценить

Проанализируем каждое из утверждений:

1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

Да, такое утверждение в геометрии есть, с дополнением » и только одну» :

«Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой, и причем только одну.»

2) Треугольник со сторонами 1, 2, 4 существует.

Для существования треугольника должно выполняться следующее правило:

Сумма двух сторон всегда больше третьей. В данном случае это не так, так как 1 + 2

pазбирался: Даниил Романович | обсудить разбор | оценить

Проанализируем каждое утверждение. 1) Это утверждение верно, поскольку равенство и перпендикулярность диагоналей является одним из свойств именно квадрата. 2) Это утверждение неверно. Основание – соответствующая теорема, которой утверждается, что смежные углы в сумме имеют 180 0 , т.е. дополняют друг друга до развернутого угла. Следовательно, равенство смежных углов может иметь место только в случае, если достоверно известно, что один из них прямой. 3) Утверждение неверно. Высотой является только биссектриса, опущенная на основание равнобедренного треугольника.

pазбирался: Даниил Романович | обсудить разбор | оценить

Выполняем анализ утверждений. 1) Согласно теореме о смежных углах, их сумма всегда равна 180 0 . Это означает, что любой из смежных углов является разностью 180 0 и величины 2-го смежного угла. Если первый смежный угол острый, значит, второй равен разности 180 0 и острого угла (т.е. угла, меньшего 90 0 ), которая в любом случае окажется больше 90 0 . А угол, больший 90 0 , по определению тупой. Итак, утверждение неверно. 2) Одно из свойств ромба заключается в том, что его диагонали перпендикулярны. Однако и диагонали квадрата тоже пересекаются под прямым углом. Но поскольку квадрат является частным случаем ромба, то и в этом противоречия заданному утверждению нет. Т.е. в целом утверждение верно. 3) Одно из основных св-в касательных к окружности заключается в том, что касательная всегда перпендикулярна к радиусу, проведенному из центра этой окружности в точку касания. Оно противоречит заданному утверждению, поэтому утверждение неверно.

pазбирался: Даниил Романович | обсудить разбор | оценить

Обращаем внимание на то, что вопрос содержит слово КАКИЕ, что означает нахождение нескольких верных ответов. Итак, первое утверждение является верным, потому что есть теорема о сумме углов треугольника, равной 180 градусов, это не зависит от вида треугольника. Второе утверждение является не верным, так как по определению, только у равнобедренной трапеции боковые стороны равны. Теперь становится понятным, что третье утверждение тоже должно быть верным. Но в доказательство тому мы имеем правила, которые нам говорят о том, что центры окружностей совпадают.

Итак, наши верные утверждения под номерами 1 и 3.

pазбирался: Даниил Романович | обсудить разбор | оценить

Видео:7 класс, 11 урок, Смежные и вертикальные углыСкачать

смежные углы всегда равны любой прямоугольник можно вписать в окружность через заданную точку

Видео:19 задание огэ математика 2023 ВСЕ ТИПЫ геометрияСкачать

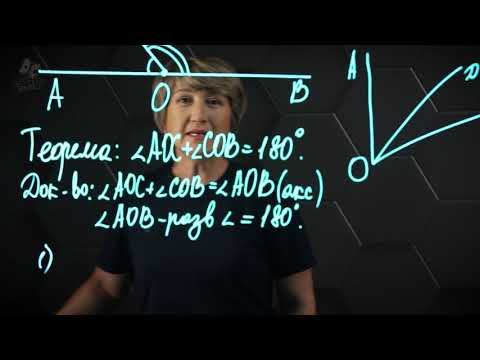
Задание №20 ОГЭ по математике

Видео:Смежные углыСкачать

Анализ геометрических высказываний

В 20 задании из приведенных утверждений необходимо выбрать одно или несколько правильных. Утверждения из общего теоретического курса геометрии, поэтому, какие-то определенные рекомендации здесь дать нельзя, кроме как полного повторения теоретического курса. Другое дело, что если вы точно не знаете какое-либо утверждение, то решить задачу можно наоборот — выбирая и отсеивая неправильные. Это задание не имеет какого либо подхода к решению, однако ниже я привел несколько разобранных задач.

Разбор типовых вариантов задания №20 ОГЭ по математике

Первый вариант задания

Какие из следующих утверждений верны?

Решение:

Все диаметры окружности всегда равны между собой — это даже интуитивно понятно. Что касается второго утверждения, то оно неверно — вписанный угол всегда в два раза меньше центрального. А вот третье утверждение тоже верно — треугольники могут быть подобны по трем углам, а у равносторонних треугольников они всегда равны.

Второй вариант задания

Какие из следующих утверждений верны?

Решение:

Первое утверждение верно, так как у равностороннего треугольника все стороны равнозначны, а значит и все элементы, проведенные к ним, тоже. Второе утверждение тоже верно, так как нет ограничений на количество произвольных прямых, проходящих через одну точку. Третье утверждение неверно — если диагонали равны, то это либо прямоугольник, либо квадрат.

Третий вариант задания

Какие из следующих утверждений верны?

Решение:

Первое утверждение верно из общих свойств треугольника — сумма двух сторон всегда больше третьей. Второе утверждение тоже верно — действительно, любой прямоугольник можно вписать в окружность. Третье утверждение неверно, так как я писал уже чуть выше, что нет ограничений на количество произвольных прямых, проходящих через одну точку.

Демонстрационный вариант ОГЭ 2019

Укажите номера верных утверждений.

Решение:

Проанализируем каждое из утверждений:

1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

Да, такое утверждение в геометрии есть, с дополнением » и только одну» :

«Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой, и причем только одну.»

2) Треугольник со сторонами 1, 2, 4 существует.

Для существования треугольника должно выполняться следующее правило:

Сумма двух сторон всегда больше третьей. В данном случае это не так, так как 1 + 2

Четвертый вариант задания

Какое из следующих утверждений верно?

1) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм является квадратом.

2) Смежные углы всегда равны.

3) Каждая из биссектрис равнобедренного треугольника является его высотой.

Решение:

Проанализируем каждое утверждение.

1) Это утверждение верно, поскольку равенство и перпендикулярность диагоналей является одним из свойств именно квадрата.

3) Утверждение неверно. Высотой является только биссектриса, опущенная на основание равнобедренного треугольника.

Пятый вариант задания

Какое из следующих утверждений верно?

1) Если угол острый, то смежный с ним угол также является острым.

2) Если диагонали параллелограмма перпендикулярны, то этот параллелограмм является ромбом.

3) Касательная к окружности параллельна радиусу, проведённому в точку касания.

Решение:

Выполняем анализ утверждений.

2) Одно из свойств ромба заключается в том, что его диагонали перпендикулярны. Однако и диагонали квадрата тоже пересекаются под прямым углом. Но поскольку квадрат является частным случаем ромба, то и в этом противоречия заданному утверждению нет. Т.е. в целом утверждение верно.

3) Одно из основных св-в касательных к окружности заключается в том, что касательная всегда перпендикулярна к радиусу, проведенному из центра этой окружности в точку касания. Оно противоречит заданному утверждению, поэтому утверждение неверно.

Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Смежные углы всегда равны любой прямоугольник можно вписать в окружность через заданную точку

Укажите номера верных утверждений.

1) Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники подобны.

2) Сумма смежных углов равна 180°.

3) Любая медиана равнобедренного треугольника является его биссектрисой.

Проверим каждое из утверждений.

1) «Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники подобны» — верно, по первому признаку подобия треугольнииков.

2) «Сумма смежных углов равна 180°» — верно, по свойству смежных углов.

3) «Любая медиана равнобедренного треугольника является его биссектрисой» — неверно; верным будет утверждение: «Любая медиана равностороннего треугольника является его биссектрисой».

Укажите номера верных утверждений.

1) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.

2) Смежные углы равны.

3) Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой.

Проверим каждое из утверждений.

1) «Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны» — верно, по второму признаку подобия треугольников.

2) «Смежные углы равны» — неверно, два смежных углы и связаны соотоношением: .

3) «Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой» — верно, по свойству равнобедренного треугольника.

Укажите номера верных утверждений.

1) Смежные углы равны.

2) Любые две прямые имеют ровно одну общую точку.

3) Если угол равен 108°, то вертикальный с ним равен 108°.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Смежные углы равны» — неверно, смежные углы и связаны соотношением: .

2) «Любые две прямые имеют ровно одну общую точку» — неверно, прямые могут также быть параллельны, тогда точек пересечения нет, или совпадать, тогда точек пересечения бесконечно много.

3) «Если угол равен 108°, то вертикальный с ним равен 108°» — верно по свойству вертикальных углов.

Аналоги к заданию № 41: 316233 Все

Укажите номера верных утверждений.

1) Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны.

2) Сумма смежных углов равна 180°.

3) Любая высота равнобедренного треугольника является его биссектрисой.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны» — верно, по признаку подобия треугольников.

2) «Сумма смежных углов равна 180°» — верно по свойству смежных углов.

3) «Любая высота равнобедренного треугольника является его биссектрисой» — неверно, это утверждение справедливо только для равностороннего треугольника.

Аналоги к заданию № 93: 171 197 311684 357582 Все

Укажите номера верных утверждений.

1) Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны.

2) Сумма смежных углов равна 180°.

3) Любая высота равнобедренного треугольника является его биссектрисой.

Проверим каждое из утверждений.

1) «Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны» — верно, по третьему признаку подобия треугольников.

2) «Сумма смежных углов равна 180°» — верно, по теореме о смежных углах.

3) «Любая высота равнобедренного треугольника является его биссектрисой» — неверно, верным будет являться утверждение «Высота равнобедренного треугольника, проведённая к его основанию, является его биссектрисой».

Какое из следующих утверждений верно?

1) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.

2) Смежные углы равны.

3) Каждая из биссектрис равнобедренного треугольника является его высотой.

Проверим каждое из утверждений.

1) «Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.» — верно, если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.

2) «Смежные углы равны.» — неверно, сумма смежных углов равна 180°.

3) «Каждая из биссектрис равнобедренного треугольника является его высотой.» — неверно, только одна биссектриса равнобедренного треугольника является его высотой.

Какие из следующих утверждений верны?

1) Треугольника со сторонами 1, 2, 4 не существует.

2) Смежные углы равны.

3) Все диаметры окружности равны между собой.

Если утверждений несколько, запишите их номера в порядке возрастания.

1) «Треугольника со сторонами 1, 2, 4 не существует» — верно, большая сторона треугольника должна быть меньше суммы двух других.

2) «Смежные углы равны» — неверно, смежные углы и связаны соотношением: .

3) «Все диаметры окружности равны между собой» — верно.

Какое из следующих утверждений верно?

1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.

2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.

3) Смежные углы равны.

Если утверждений несколько, запишите их номера в порядке возрастания.

1) «Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой» — верно, это аксиома планиметрии.

2) «Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны» — неверно: например, могут быть квадрат и ромб с равной длиной стороны.

3) «Смежные углы равны» — неверно, смежные углы и связаны соотношением: .

Окружность проходит через вершины А и С треугольника АВС и пересекает его стороны АВ и ВС в точках К и Е соответственно. Отрезки АЕ и СК перпендикулярны. Найдите ∠КСВ, если ∠АВС = 20°.

Углы АКС и АЕС равны, т. к. опираются на одну дугу окружности; следовательно, ∠ВКС = ∠ВЕА, как смежные с ними. Из четырёхугольника ВКDЕ: Из ВКС: ∠КСВ = 180° − 125° − 20° = 35°.

Какое из следующих утверждений верно?

1. Всегда один из двух смежных углов острый, а другой тупой.

2. Площадь квадрата равна произведению двух его смежных сторон.

3. Все хорды одной окружности равны между собой.

В ответ запишите номер выбранного утверждения.

Рассмотрим каждое из утверждений:

Какое из следующих утверждений верно?

1) В прямоугольном треугольнике гипотенуза равна сумме катетов.

2) Всегда один из двух смежных углов острый, а другой тупой.

3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.

В ответ запишите номер выбранного утверждения.

Рассмотрим каждое из утверждений:

1) «В прямоугольном треугольнике гипотенуза равна сумме катетов» — неверно, по теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

2) «Всегда один из двух смежных углов острый, а другой тупой» — неверно, так как сумма смежных углов равна 180°, следовательно, если один из углов прямой, то смежный ему будет тоже прямой.

3) «Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности» — верно по свойству окружности.

Какие из следующих утверждений верны?

1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.

2) Если угол равен 60°, то смежный с ним равен 120°.

3) Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.

4) Через любые три точки проходит не более одной прямой.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.» — неверно, если при пересечении двух прямых третьей прямой внутренние накрестлежащие углы равны, то эти две прямые параллельны. Если внутренние накрестлежащие углы составляют в сумме 90°, то они могут быть не равны.

2) «Если угол равен 60°, то смежный с ним равен 120°.» — верно, сумма смежных углов равна 180°.

3) «Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.» — верно, если при пересечении двух прямых третьей прямой внутренние односторонние углы составляют в сумме 180°, то эти две прямые параллельны.

4) «Через любые три точки проходит не более одной прямой.» — верно, через три точки либо нельзя провести прямую, если они не лежат на одной линии, либо можно, но только одну.

Какие из следующих утверждений верны?

1) Смежные углы всегда равны.

2) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.

3) Любые два равносторонних треугольника подобны.

В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

1) Смежные углы всегда равны. — неверно, сумма смежных углов равна 180°.

2) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой. — верно.

3) Любые два равносторонних треугольника подобны. — верно, они подобны по второму признаку подобия.

Какое из следующих утверждений верно?

1) Смежные углы всегда равны.

2) Каждая из биссектрис равнобедренного треугольника является его высотой.

3) Существует прямоугольник, диагонали которого взаимно перпендикулярны.

Проверим каждое из утверждений.

1) «Смежные углы равны» — неверно, смежные углы и связаны соотношением: .

2) «Каждая из биссектрис равнобедренного треугольника является его высотой» — неверно, верным будет являться утверждение: «Каждая из биссектрис равностороннего треугольника является его высотой».

3) «Существует прямоугольник, диагонали которого взаимно перпендикулярны.» — верно, такой прямоугольник — это квадрат.

Какие из данных утверждений верны? Запишите их номера.

2) В любой треугольник можно вписать окружность.

3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.

Проверим каждое из утверждений.

2) «В любой треугольник можно вписать окружность» — верно, по свойству треугольника.

3) «Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом» — верно, поскольку если его смежные стороны равны, то и все его стороны равны..

Какие из данных утверждений верны? Запишите их номера.

1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.

2) Диагональ трапеции делит её на два равных треугольника.

3) Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон.

Проверим каждое из утверждений.

1) «Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны» — верно, по признаку параллельности прямых.

2) «Диагональ трапеции делит её на два равных треугольника» — неверно, верным будет утверждение «Диагональ параллелограмма делит его на два равных треугольника».

3) «Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон» — верно, по теореме Пифагора.

Укажите номера верных утверждений.

1) Если угол равен 47°, то смежный с ним равен 153°.

2) Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.

3) Через любую точку проходит ровно одна прямая.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Если угол равен 47°, то смежный с ним равен 153°» — неверно, сумма смежных углов равна 180°.

2) «Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны» — верно, по признаку параллельности прямых.

3) «Через любую точку проходит ровно одна прямая» — неверно через одну точку проходит бесконечное множество прямых.

Не следует думать, что вопрос «какие утверждения верные?» подразумевает, что в ответе должно быть несколько утверждений. Так же, как задача «решите уравнение» не подразумевает, что решение вообще есть.

Укажите номера верных утверждений.

1) Любые три прямые имеют не более одной общей точки.

2) Если угол равен 120°, то смежный с ним равен 120°.

3) Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведённой из данной точки к прямой, больше 3.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Любые три прямые имеют не более одной общей точки» — верно. Если прямые имеют две и более общих точек, то они совпадают. (См. комментарии к задаче.)

2) «Если угол равен 120°, то смежный с ним равен 120°» — неверно. Сумма смежных углов равна 180°.

3) «Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведённой из данной точки к прямой, больше 3» — верно. Т. к. расстояние — длина кратчайшего отрезка до прямой, а все наклонные — длиннее.

Аналоги к заданию № 311851: 316323 316349 316375 Все

В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ВАС. Ответ дайте в градусах.

Сумма смежных углов равна 180°, поэтому В равнобедренном треугольнике углы при основании равны, следовательно,

Аналоги к заданию № 37: 311680 340586 Все

Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.

Запишите величины углов в ответ без пробелов в порядке неубывания.

Пусть углы трапеции равны и угол Около выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма противоположных углов равна 180°: откуда Сумма смежных углов в трапеции равна 180°, следовательно, Тем самым, три неизвестных угла равны 49°, 131° и 131°.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

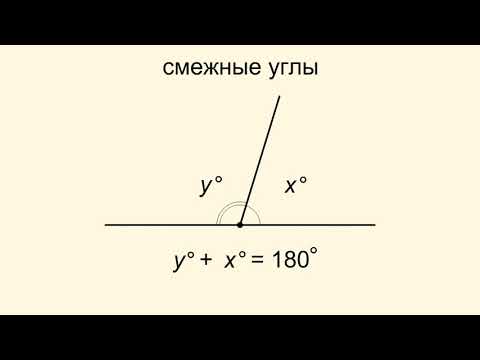
Смежные углы всегда равны любой прямоугольник можно вписать в окружность через заданную точку

Какие из данных утверждений верны? Запишите их номера.

1) Площадь квадрата равна произведению его диагоналей.

2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.

3) Вокруг любого параллелограмма можно описать окружность.

Проверим каждое из утверждений.

2) «Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны» — верно, по признаку параллельности прямых.

3) «Вокруг любого параллелограмма можно описать окружность» — неверно, т. к. вокруг параллелограмма можно описать окружность только если сумма его противоположных углов равна 180°..

Какое из следующих утверждений верно?

1) Сумма углов выпуклого четырёхугольника равна 360 градусам.

2) Средняя линия трапеции равна сумме её оснований.

3) Любой параллелограмм можно вписать в окружность.

Проверим каждое из утверждений.

1) «Сумма углов выпуклого четырёхугольника равна 360 градусам.» — верно, по теореме о сумме углов выпуклого многоугольника сумма углов n-угольника равна 180°(n − 2). Следовательно, сумма углов выпуклого четырёхугольника равна 360 градусам.

2) «Средняя линия трапеции равна сумме её оснований.» — неверно, Средняя линия трапеции равна полусумме её оснований.

3) «Любой параллелограмм можно вписать в окружность.» — неверно, в окружность можно вписать только четырёхугольник, сумма противоположенных углов которого равна 180°.

Какое из следующих утверждений верно?

1) Площадь параллелограмма равна половине произведения его диагоналей.

2) Сумма углов прямоугольного треугольника равна 90 градусам.

3) Биссектрисы треугольника пересекаются в центре вписанной в него окружности.

Проверим каждое из утверждений.

1) «Площадь параллелограмма равна половине произведения его диагоналей.» — неверно, площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.

2) «Сумма углов прямоугольного треугольника равна 90 градусам.» — неверно, Сумма углов прямоугольного треугольника равна 180 градусам.

3) «Биссектрисы треугольника пересекаются в центре вписанной в него окружности.» — верно, биссектрисы треугольника пересекаются в центре вписанной в него окружности.

Какое из следующих утверждений верно?

1) Любой прямоугольник можно вписать в окружность.

2) Все углы ромба равны.

3) Треугольник со сторонами 1, 2, 4 существует.

Проверим каждое из утверждений.

1) « Любой прямоугольник можно вписать в окружность.» — верно, выпуклый четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположныхх углов этого четырёхугольника равна 180°.

2) «Все углы ромба равны.» — неверно, противоположные углы ромба равны.

3) «Треугольник со сторонами 1, 2, 4 существует.» — неверно, для того, чтобы существовал треугольник, сумма любых его двух сторон должна быть больше третьей стороны.

Какое из следующих утверждений верно?

1) Все равнобедренные треугольники подобны.

2) Существует прямоугольник, диагонали которого взаимно перпендикулярны.

3) Сумма углов прямоугольного треугольника равна 90 градусам.

Проверим каждое из утверждений.

1) «Все равнобедренные треугольники подобны.» — неверно, не все равнобедренные треугольники подобны.

2) «Существует прямоугольник, диагонали которого взаимно перпендикулярны.» — верно, такой прямоугольник — это квадрат.

3) «Сумма углов прямоугольного треугольника равна 90 градусам.» — неверно, сумма острых углов прямоугольного треугольника равна 90 градусам.

Какое из следующих утверждений верно?

1. Диагонали параллелограмма равны.

2. Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.

3. Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.

Рассмотрим каждое из утверждений:

Какие из следующих утверждений верны?

1. Треугольника со сторонами 1, 2, 4 не существует.

2. Медиана треугольника делит пополам угол, из вершины которого проведена.

3. Все диаметры окружности равны между собой.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Рассмотрим каждое из утверждений:

Какие из следующих утверждений верны?

1.Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.

2.Площадь трапеции равна произведению основания трапеции на высоту.

3.Треугольника со сторонами 1, 2, 4 не существует.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Рассмотрим каждое из утверждений:

Какие из следующих утверждений верны?

1) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.

2) Боковые стороны любой трапеции равны.

3) Один из углов треугольника всегда не превышает 60 градусов.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Рассмотрим каждое из утверждений:

1) «Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне» — верно, так как ромб — это частный случай параллелограмма и его площадь есть произведение его стороны на высоту, проведённую к этой стороне.

2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.

3) «Один из углов треугольника всегда не превышает 60 градусов» — верно, наименьший угол в любом треугольнике всегда не превышает 60 градусов.

Какие из следующих утверждений верны?

1) Один из углов треугольника всегда не превышает 60 градусов.

2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.

3) Две прямые, параллельные третьей прямой, перпендикулярны.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Рассмотрим каждое из утверждений:

1) «Один из углов треугольника всегда не превышает 60 градусов» — верно, наименьший угол в любом треугольнике всегда не превышает 60 градусов.

3) «Две прямые, параллельные третьей прямой, перпендикулярны» — неверно, две прямые, параллельные третьей прямой, параллельны.

Какие из следующих утверждений верны?

1) Все высоты равностороннего треугольника равны.

2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.

3) В любой ромб можно вписать окружность.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Все высоты равностороннего треугольника равны» — верно, так как в равностороннем треугольнике все высоты равны между собой.

2) «Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу» — неверно, так как угол, вписанный в окружность, равен половине соответствующего центрального угла, опирающегося на ту же дугу.

3) «В любой ромб можно вписать окружность» — верно, так как суммы противоположных сторон ромба равны.

Какие из следующих утверждений верны?

1) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.

2) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.

3) Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°.

4) Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.» — верно, если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.

2) «Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.» — верно, если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.

3) «Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°.» — неверно, стороны параллелограмма параллельны и образуют односторонние углы, а сумма односторонних углов равна 180°.

4) «Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.» — верно, сумма углов выпуклого четырехугольника равна 360°.

Какие из данных утверждений верны? Запишите их номера.

1) Каждая из биссектрис равнобедренного треугольника является его высотой.

2) Диагонали прямоугольника равны.

3) У любой трапеции основания параллельны.

Проверим каждое из утверждений.

1) «Каждая из биссектрис равнобедренного треугольника является его высотой» — неверно, верным будет являться утверждение: «Каждая из биссектрис равностороннего треугольника является его высотой».

2) «Диагонали прямоугольника равны» — верно по свойству диагоналей прямоугольника.

3) «У любой трапеции основания параллельны» — верно по определению трапеции.

Какие из следующих утверждений верны?

1) Один из углов треугольника всегда не превышает 60 градусов.

2) Диагонали трапеции пересекаются и делятся точкой пересечения пополам.

3) Все диаметры окружности равны между собой.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Один из углов треугольника всегда не превышает 60 градусов» — верно, сумма всех углов в треугольнике равна 180°, значит, меньший угол в треугольнике . Следовательно, в любом треугольнике есть угол, не превышающий 60 градусов, а значит, один из углов любого треугольника не превышает 60 градусов.

2) «Диагонали трапеции пересекаются и делятся точкой пересечения пополам» — неверно.

3) «Все диаметры окружности равны между собой» — верно.

Какие из следующих утверждений верны?

1. Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.

2. Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.

3. Если диагонали параллелограмма равны, то этот параллелограмм является ромбом.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Рассмотрим каждое из утверждений:

Какие из следующих утверждений верны?

1) Существуют три прямые, которые проходят через одну точку.

2) Боковые стороны любой трапеции равны.

3) Сумма углов равнобедренного треугольника равна 180 градусам.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.

2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.

3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.

Какие из следующих утверждений верны?

1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.

2) Если угол равен 60°, то смежный с ним равен 120°.

3) Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.

4) Через любые три точки проходит не более одной прямой.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.» — неверно, если при пересечении двух прямых третьей прямой внутренние накрестлежащие углы равны, то эти две прямые параллельны. Если внутренние накрестлежащие углы составляют в сумме 90°, то они могут быть не равны.

2) «Если угол равен 60°, то смежный с ним равен 120°.» — верно, сумма смежных углов равна 180°.

3) «Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.» — верно, если при пересечении двух прямых третьей прямой внутренние односторонние углы составляют в сумме 180°, то эти две прямые параллельны.

4) «Через любые три точки проходит не более одной прямой.» — верно, через три точки либо нельзя провести прямую, если они не лежат на одной линии, либо можно, но только одну.

Какие из следующих утверждений верны?

1) Через любые три точки проходит не более одной окружности.

2) Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек.

3) Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются.

4) Если дуга окружности составляет 80°, то вписанный угол, опирающийся на эту дугу окружности, равен 40°.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Через любые три точки проходит не более одной окружности.» — верно, Через любые три точки, не лежащие на одной прямой, проходит единственная окружность. Если точки лежат на одной прямой, то окружность провести невозможно. Тем самым, через любые три точки можно провести не более одной окружности.

2) «Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек.» — верно, если расстояние от центра до прямой меньше радиуса, то окружности имеют две общие точки, если окружности касаются то окружности имеют одну общую точку, если расстояние больше радиуса, то окружности не имеют общих точек.

3) «Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются» — неверно, окружность, радиус которой равен 3, лежит внутри окружности с радиусом 5.

4) «Если дуга окружности составляет 80°, то вписанный угол, опирающийся на эту дугу окружности, равен 40°.» — верно, вписанный угол измеряется половиной дуги,на которую он опирается.

💡 Видео

Задачи: смежные и вертикальные углы. 4 задачи за 7 минут. Все о смежных и вертикальных углахСкачать

СМЕЖНЫЕ ВЕРТИКАЛЬНЫЕ УГЛЫ геометрия 7 класс. Теорема, доказательствоСкачать

Задачка про смежные углы. Геометрия 7 класс.Скачать

Смежные и вертикальные углы. Практическая часть - решение задачи. 7 класс.Скачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Вертикальные и смежные углы. Геометрия 7 класс.Скачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Математика за 2 минуты: СМЕЖНЫЕ УГЛЫ // ГеометрияСкачать

все, что нужно знать для 16 задачи | вся планиметрия в одном видеоСкачать

ВСЕ ТИПЫ 19 задания на ОГЭ по математике 2024 | Дядя АртёмСкачать

Смежные углы. Геометрия 7 класс.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Вся геометрия 7–9 класс с нуля | ОГЭ МАТЕМАТИКА 2023Скачать